机器学习实战—— Chap08.Regression

Linear Regression

import matplotlib.pyplot as plt
import numpy as np

"""
Desc:
    加载数据

Parameters:
    filename - 文件名
    
Returns:
    xArr - x数据集
    yArr - y数据集
"""
def loadDataSet(filename):
    # 计算特征个数，由于最后一列为y值所以减一
    numFeat = len(open(filename).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


"""
Desc:
    计算回归系数w

Parameters:
    xArr - x数据集
    yArr - y数据集
    
Returns:
    ws - 回归系数
"""
def standRegres(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    xTx = xMat.T * xMat
    # 求矩阵的行列式
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (xTx.I) * (xMat.T) * yMat
    return ws


"""
Desc:
    绘制数据集

Parameters:
    None
    
Returns:
    None
"""
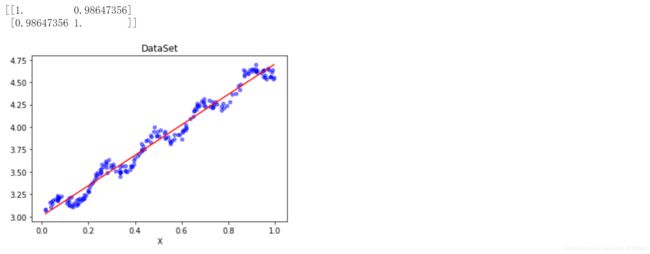
def plotDataSet():
    xArr, yArr = loadDataSet('ex0.txt')
    ws = standRegres(xArr, yArr)
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xCopy = xMat.copy()
    # 排序
    xCopy.sort(0)
    yHat = xCopy * ws
    # 以下两行是通过corrcoef函数比较预测值和真实值的相关性
    # corrcoef函数得到相关系数矩阵
    # 得到的结果中对角线上的数据是1.0，因为yMat和自己的匹配是完美的
    # 而yHat1和yMat的相关系数为0.98
    yHat1 = xMat * ws
    print(np.corrcoef(yHat1.T, yMat))
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(xCopy[:, 1], yHat, c='red')
    # 绘制样本点即
    # flatten返回一个折叠成一维的数组。但是该函数只能适用于numpy对象，即array或者mat，普通的list列表是不行的
    # 矩阵.A(等效于矩阵.getA())变成了数组
    ax.scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)
    plt.title('DataSet')
    plt.xlabel('X')
    plt.show()
    
    
if __name__ == '__main__':
    plotDataSet()
    

from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np

"""
Desc:
    加载数据

Parameters:
    filename - 文件名
    
Returns:
    xArr - x数据集
    yArr - y数据集
"""
def loadDataSet(filename):
    # 计算特征个数，由于最后一列为y值所以减一
    numFeat = len(open(filename).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


"""
Desc:
    使用局部加权线性回归计算回归系数w

Parameters:
    testPoint - 测试样本点
    xArr - x数据集
    yArr - y数据集
    k - 高斯核的k，自定义参数
    
Returns:
    ws - 回归系数
"""
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    # 创建加权对角阵
    weights = np.mat(np.eye((m)))
    for j in range(m):
        # 高斯核
        diffMat = testPoint - xMat[j, :]
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0 * k**2))
    xTx = xMat.T * (weights * xMat)
    # 求矩阵的行列式
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (xTx.I) * (xMat.T * (weights * yMat))
    return testPoint * ws


"""
Desc:
    局部加权线性回归测试

Parameters:
    testArr - 测试数据集
    xArr - x数据集
    yArr - y数据集
    k - 高斯核的k,自定义参数
    
Returns:
    ws - 回归系数
"""
def lwlrTest(testArr, xArr, yArr, k=1.0):
    m = np.shape(testArr)[0]
    yHat = np.zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat


"""
Desc:
    绘制多条局部加权回归曲线

Parameters:
    None
    
Returns:
    None
"""
def plotlwlrRegression():
    # 设置中文字体
    font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
    xArr, yArr = loadDataSet('ex0.txt')
    yHat_1 = lwlrTest(xArr, xArr, yArr, 1.0)
    yHat_2 = lwlrTest(xArr, xArr, yArr, 0.01)
    yHat_3 = lwlrTest(xArr, xArr, yArr, 0.003)
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    # 排序，返回索引值
    srtInd = xMat[:, 1].argsort(0)
    xSort = xMat[srtInd][:, 0, :]
    fig, axs = plt.subplots(nrows=3, ncols=1, sharex=False, sharey=False, figsize=(10, 8))
    axs[0].plot(xSort[:, 1], yHat_1[srtInd], c='red')
    axs[1].plot(xSort[:, 1], yHat_2[srtInd], c='red')
    axs[2].plot(xSort[:, 1], yHat_3[srtInd], c='red')
    axs[0].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)
    axs[1].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)
    axs[2].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)
    axs0_title_text = axs[0].set_title(u'局部加权回归曲线,k=1.0', FontProperties=font)
    axs1_title_text = axs[1].set_title(u'局部加权回归曲线,k=0.01', FontProperties=font)
    axs2_title_text = axs[2].set_title(u'局部加权回归曲线,k=0.003', FontProperties=font)
    plt.setp(axs0_title_text, size=8, weight='bold', color='red')
    plt.setp(axs1_title_text, size=8, weight='bold', color='red')
    plt.setp(axs2_title_text, size=8, weight='bold', color='red')
    plt.xlabel('X')
    plt.show()
    
    
if __name__ == '__main__':
    plotlwlrRegression()

import numpy as np

"""
Desc:
    加载数据

Parameters:
    filename - 文件名
    
Returns:
    xArr - x数据集
    yArr - y数据集
"""
def loadDataSet(filename):
    # 计算特征个数，由于最后一列为y值所以减一
    numFeat = len(open(filename).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


"""
Desc:
    使用局部加权线性回归计算回归系数w

Parameters:
    testPoint - 测试样本点
    xArr - x数据集
    yArr - y数据集
    k - 高斯核的k，自定义参数
    
Returns:
    ws - 回归系数
"""
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    # 创建加权对角阵
    weights = np.mat(np.eye((m)))
    for j in range(m):
        # 高斯核
        diffMat = testPoint - xMat[j, :]
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0 * k**2))
    xTx = xMat.T * (weights * xMat)
    # 求矩阵的行列式
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (xTx.I) * (xMat.T * (weights * yMat))
    return testPoint * ws


"""
Desc:
    局部加权线性回归测试

Parameters:
    testArr - 测试数据集
    xArr - x数据集
    yArr - y数据集
    k - 高斯核的k,自定义参数
    
Returns:
    ws - 回归系数
"""
def lwlrTest(testArr, xArr, yArr, k=1.0):
    m = np.shape(testArr)[0]
    yHat = np.zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat


"""
Desc:
    计算回归系数w

Parameters:
    xArr - x数据集
    yArr - y数据集
    
Returns:
    ws - 回归系数
"""
def standRegres(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    xTx = xMat.T * xMat
    # 求矩阵的行列式
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (xTx.I) * (xMat.T) * yMat
    return ws


"""
Desc:
    误差大小评价函数

Parameters:
    yArr - 真实数据
    yHatArr - 预测数据
    
Returns:
    ws - 回归系数
"""
def rssError(yArr, yHatArr):
    return ((yArr - yHatArr)**2).sum()


if __name__ == '__main__':
    abX, abY = loadDataSet('abalone.txt')
    print("训练集与测试集相同:局部加权线性回归,核k的大小对预测的影响:")
    yHat01 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为：', rssError(abY[0:99], yHat01.T))
    print('k=1时,误差大小为：', rssError(abY[0:99], yHat1.T))
    print('k=10时,误差大小为：', rssError(abY[0:99], yHat10.T))
    print('')
    print("训练集与测试集不同：局部加权线性回归，核k的大小是越小越好吗？更换数据集，测试结果如下：")
    yHat01 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为：', rssError(abY[100:199], yHat01.T))
    print('k=1时,误差大小为：', rssError(abY[100:199], yHat1.T))
    print('k=10时,误差大小为：', rssError(abY[100:199], yHat10.T))
    print('')
    print("训练集与测试集不同：简单的线性回归与k=1时的局部加权线性回归对比：")
    print('k=1时,误差大小为：', rssError(abY[100:199], yHat1.T))
    ws = standRegres(abX[0:99], abY[0:99])
    yHat = np.mat(abX[100:199]) * ws
    print('简单的线性回归误差大小:', rssError(abY[100:199], yHat.T.A))

import numpy as np
from bs4 import BeautifulSoup
import random

"""
Desc:
    从页面读取数据，生成retX和retY列表

Parameters:
    retX - 数据X
    retY - 数据Y
    inFile - HTML文件
    yr - 年份
    numPce - 乐高部件数目
    origPrc - 原价
    
Returns:
    None
"""
def scrapePage(retX, retY, inFile, yr, numPce, origPrc):
    # 打开并读取HTML文件
    with open(inFile, encoding='utf-8') as f:
        html = f.read()
    soup = BeautifulSoup(html)
    i = 1
    # 根据HTML页面结构进行解析
    currentRow = soup.find_all('table', r='%d' % i)
    while(len(currentRow) != 0):
        currentRow = soup.find_all('table', r='%d' % i)
        title = currentRow[0].find_all('a')[1].text
        lwrTitle = title.lower()
        # 查找是否有全新标签
        if(lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
            newFlag = 1.0
        else:
            newFlag = 0.0
        # 查找是否已经标志出售，我们只收集已出售的数据
        soldUnicde = currentRow[0].find_all('td')[3].find_all('span')
        if len(soldUnicde) == 0:
            print("商品#%d没有出售" % i)
        else:
            # 解析页面获取当前价格
            soldPrice = currentRow[0].find_all('td')[4]
            priceStr = soldPrice.text
            priceStr = priceStr.replace('$', '')
            priceStr = priceStr.replace(',', '')
            if len(soldPrice) > 1:
                priceStr = priceStr.replace('Free shipping', '')
            sellingPrice = float(priceStr)
            # 去掉不完整的套装价格
            if sellingPrice > origPrc * 0.5:
                print('%d\t%d\t%d\t%f\t%f' % (yr, numPce, newFlag, origPrc, sellingPrice))
                retX.append([yr, numPce, newFlag, origPrc])
                retY.append(sellingPrice)
        i += 1
        currentRow = soup.find_all('table', r='%d' % i)


"""
Desc:
    依次读取六种乐高套装的数据，并生成数据矩阵

Parameters:
    retX - 数据X
    retY - 数据Y
    
Returns:
    None
"""
def setDataCollect(retX, retY):
    # 2006年的乐高8288，部件数目800，原价49.99
    scrapePage(retX, retY, './lego/lego8288.html', 2006, 800, 49.99)
    scrapePage(retX, retY, './lego/lego10030.html', 2002, 3096, 269.99)
    scrapePage(retX, retY, './lego/lego10179.html', 2007, 5195, 499.99)
    scrapePage(retX, retY, './lego/lego10181.html', 2007, 3428, 199.99)
    scrapePage(retX, retY, './lego/lego10189.html', 2008, 5922, 299.99)
    scrapePage(retX, retY, './lego/lego10196.html', 2009, 3263, 249.99)


"""
Desc:
    数据标准化

Parameters:
    xMat - x数据集
    yMat - y数据集
    
Returns:
    inxMat - 标准化后的x数据集
    inyMat - 标准化后的y数据集
"""
def regularize(xMat, yMat):
    # 深层拷贝
    inxMat = xMat.copy()
    inyMat = yMat.copy()
    # 求yMat的均值
    yMean = np.mean(yMat, 0)
    # 计算yMat每一个值与yMean的差值
    inyMat = yMat - yMean
    # 求inxMat每一列的均值
    inMeans = np.mean(inxMat, 0)
    # 求inxMat每一列的方差即（各项-均值的平方求和）后再除以N
    inVar = np.var(inxMat, 0)
    print(inMeans)
    # 数据减去均值处以方差实现标准化
    inxMat = (inxMat - inMeans) / inVar
    return inxMat, inyMat


"""
Desc:
    计算平方误差

Parameters:
    yArr - 预测值
    yHatArr - 真实值
    
Returns:
    平方误差
"""
def rssError(yArr, yHatArr):
    return ((yArr - yHatArr)**2).sum()


"""
Desc:
    计算回归系数w

Parameters:
    xArr - x数据集
    yArr - y数据集
    
Returns:
    ws - 回归系数
"""
def standRegres(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    xTx = xMat.T * xMat
    # 求矩阵的行列式
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (xTx.I) * (xMat.T) * yMat
    return ws


"""
Desc:
    岭回归

Parameters:
    xMat - x数据集
    yMat - y数据集
    lam - 缩减系数
    
Returns:
    ws - 回归系数
"""
def ridgeRegres(xMat, yMat, lam=0.2):
    xTx = xMat.T * xMat
    demon = xTx + np.eye(np.shape(xMat)[1]) * lam
    # 求矩阵的行列式
    if np.linalg.det(demon) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (demon.I) * (xMat.T) * yMat
    return ws


"""
Desc:
    岭回归测试

Parameters:
    xArr - x数据集
    yArr - y数据集
    
Returns:
    wMat - 回归系数矩阵
"""
def ridgeTest(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    # 数据标准化
    # 行与行操作，求均值
    yMean = np.mean(yMat, axis=0)
    # 数据减去均值
    yMat = yMat - yMean
    # 行与行操作，求均值
    xMeans = np.mean(xMat, axis=0)
    # 行与行操作，求方差
    xVar = np.var(xMat, axis=0)
    # 数据减去均值除以方差实现标准化
    xMat = (xMat - xMeans) / xVar
    # 30个不同的lamda测试
    numTestPts = 30
    # 初始化回归系数矩阵
    wMat = np.zeros((numTestPts, np.shape(xMat)[1]))
    # 改变lamda计算回归系数
    for i in range(numTestPts):
        # lamda以e的指数变化，最初是一个非常小的数
        ws = ridgeRegres(xMat, yMat, np.exp(i - 10))
        # 计算回归系数矩阵
        wMat[i, :] = ws.T
    return wMat


"""
Desc:
    使用简单的线性回归

Parameters:
    None
    
Returns:
    None
"""
def useStandRegres():
    lgX = []
    lgY = []
    setDataCollect(lgX, lgY)
    data_num, features_num = np.shape(lgX)
    # 第一列全为1
    lgx1 = np.mat(np.ones((data_num, features_num+1)))
    lgx1[:, 1:5] = np.mat(lgX)
    # 计算回归系数
    ws = standRegres(lgx1, lgY)
    print("%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价" % (ws[0], ws[1], ws[2], ws[3], ws[4]))
    

"""
Desc:
    交叉验证岭回归

Parameters:
    xArr - x数据集
    yArr - y数据集
    numVal - 交叉验证次数
    
Returns:
    wMat - 回归系数矩阵
"""
def crossValidation(xArr, yArr, numVal=10):
    m = len(yArr)
    indexList = list(range(m))
    errorMat = np.zeros((numVal, 30))
    for i in range(numVal):
        trainX = []
        trainY = []
        testX = []
        testY = []
        # shuffle() 方法将序列的所有元素随机排序。
        random.shuffle(indexList)
        for j in range(m):
            # 90%数据训练集
            if j < m * 0.9:
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            # 10%数据测试集
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        # 岭回归测试
        wMat = ridgeTest(trainX, trainY)
        for k in range(30):
            matTestX = np.mat(testX)
            matTrainX = np.mat(trainX)
            # 标准化
            meanTrain = np.mean(matTrainX, 0)
            varTrain = np.var(matTrainX, 0)
            matTestX = (matTestX - meanTrain) / varTrain
            # 数据还原
            yEst = matTestX * np.mat(wMat[k, :]).T + np.mean(trainY)
            errorMat[i, k] = rssError(yEst.T.A, np.array(testY))
    meanErrors = np.mean(errorMat, 0)
    minMean = float(min(meanErrors))
    bestWeights = wMat[np.nonzero(meanErrors == minMean)]
    # 表转换
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    meanX = np.mean(xMat, 0)
    varX = np.var(xMat, 0)
    unReg = bestWeights / varX
    print("%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价" % ((-1 * np.sum(np.multiply(meanX, unReg)) + np.mean(yMat)), unReg[0, 0], unReg[0, 1], unReg[0, 2], unReg[0, 3]))
    
 
if __name__ == '__main__':
    # useStandRegres()
    lgX = []
    lgY = []
    setDataCollect(lgX, lgY)
    print(ridgeTest(lgX, lgY))
    crossValidation(lgX, lgY)

Ridge Regression

from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np

"""
Desc:
    加载数据

Parameters:
    filename - 文件名
    
Returns:
    xArr - x数据集
    yArr - y数据集
"""
def loadDataSet(filename):
    # 计算特征个数，由于最后一列为y值所以减一
    numFeat = len(open(filename).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


"""
Desc:
    岭回归

Parameters:
    xMat - x数据集
    yMat - y数据集
    lam - 缩减系数
    
Returns:
    ws - 回归系数
"""
def ridgeRegres(xMat, yMat, lam=0.2):
    xTx = xMat.T * xMat
    demon = xTx + np.eye(np.shape(xMat)[1]) * lam
    # 求矩阵的行列式
    if np.linalg.det(demon) == 0.0:
        print("矩阵为奇异矩阵，不能求逆")
        return
    # .I求逆矩阵
    ws = (demon.I) * (xMat.T) * yMat
    return ws


"""
Desc:
    岭回归测试

Parameters:
    xArr - x数据集
    yArr - y数据集
    
Returns:
    wMat - 回归系数矩阵
"""
def ridgeTest(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    # 数据标准化
    # 行与行操作，求均值
    yMean = np.mean(yMat, axis=0)
    # 数据减去均值
    yMat = yMat - yMean
    # 行与行操作，求均值
    xMeans = np.mean(xMat, axis=0)
    # 行与行操作，求方差
    xVar = np.var(xMat, axis=0)
    # 数据减去均值除以方差实现标准化
    xMat = (xMat - xMeans) / xVar
    # 30个不同的lamda测试
    numTestPts = 30
    # 初始化回归系数矩阵
    wMat = np.zeros((numTestPts, np.shape(xMat)[1]))
    # 改变lamda计算回归系数
    for i in range(numTestPts):
        # lamda以e的指数变化，最初是一个非常小的数
        ws = ridgeRegres(xMat, yMat, np.exp(i - 10))
        # 计算回归系数矩阵
        wMat[i, :] = ws.T
    return wMat


"""
Desc:
    绘制岭回归系数矩阵

Parameters:
    None
    
Returns:
    None
"""
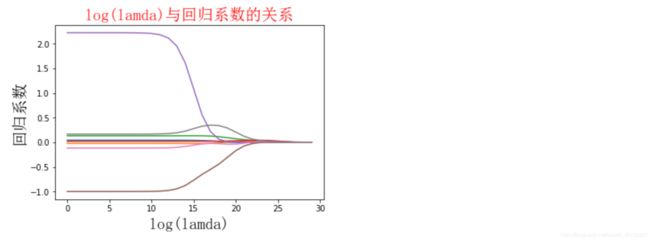
def plotwMat():
    # 设置中文字体
    font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
    abX, abY = loadDataSet('abalone.txt')
    redgeWeights = ridgeTest(abX, abY)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(redgeWeights)
    ax_title_text = ax.set_title(u'log(lamda)与回归系数的关系', FontProperties=font)
    ax_xlabel_text = ax.set_xlabel(u'log(lamda)', FontProperties=font)
    ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties=font)
    plt.setp(ax_title_text, size=20, weight='bold', color='red')
    plt.setp(ax_xlabel_text, size=20, weight='bold', color='black')
    plt.setp(ax_ylabel_text, size=20, weight='bold', color='black')
    plt.show()


if __name__ == '__main__':
    plotwMat()

from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np

"""
Desc:
    加载数据

Parameters:
    filename - 文件名
    
Returns:
    xArr - x数据集
    yArr - y数据集
"""
def loadDataSet(filename):
    # 计算特征个数，由于最后一列为y值所以减一
    numFeat = len(open(filename).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


"""
Desc:
    数据标准化

Parameters:
    xMat - x数据集
    yMat - y数据集
    
Returns:
    inxMat - 标准化后的x数据集
    inyMat - 标准化后的y数据集
"""
def regularize(xMat, yMat):
    inxMat = xMat.copy()
    inyMat = yMat.copy()
    # 求yMat的均值
    yMean = np.mean(yMat, 0)
    # 计算yMat每一个值与yMean的差值
    inyMat = yMat - yMean
    # 求inxMat每一列的均值
    inMeans = np.mean(inxMat, 0)
    # 求inxMat每一列的方差即（各项-均值的平方求和）后再除以N
    inVar = np.var(inxMat, 0)
    # 数据减去均值处以方差实现标准化
    inxMat = (inxMat - inMeans) / inVar
    return inxMat, inyMat


"""
Desc:
    计算平方误差

Parameters:
    yArr - 预测值
    yHatArr - 真实值
    
Returns:
    平方误差
"""
def rssError(yArr, yHatArr):
    return ((yArr - yHatArr)**2).sum()


"""
Desc:
    前向逐步线性回归

Parameters:
    xArr - x输入数据
    yArr - y输入数据
    eps - 每次迭代需要调整的步长
    numIt - 迭代次数
    
Returns:
    returnMat - numIt次迭代的回归系数矩阵
"""
def stageWise(xArr, yArr, eps=0.01, numIt=100):
    # 使xMat和yMat的行数一致
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    # 标准化
    xMat, yMat = regularize(xMat, yMat)
    m, n = np.shape(xMat)
    returnMat = np.zeros((numIt, n))
    ws = np.zeros((n, 1))
    wsTest = ws.copy()
    wsMax = ws.copy()
    for i in range(numIt):
        lowestError = float('inf')
        for j in range(n):
            for sign in [-1, 1]:
                wsTest = ws.copy()
                # 微调回归系数
                wsTest[j] += eps * sign
                # 计算预测值
                yTest = xMat * wsTest
                # 计算平方误差
                rssE = rssError(yMat.A, yTest.A)
                # 如果误差更小则更新当前的最佳回归系数
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        # 记录numIt次迭代的回归系数矩阵
        returnMat[i, :] = ws.T
    return returnMat


"""
Desc:
    绘制岭回归系数矩阵

Parameters:
    None
    
Returns:
    None
"""
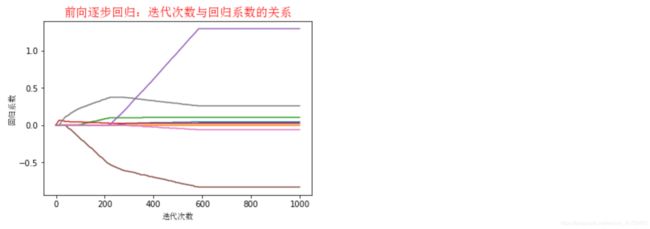
def plotstageWiseMat():
    # 设置中文字体
    font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
    xArr, yArr = loadDataSet('abalone.txt')
    returnMat = stageWise(xArr, yArr, 0.005, 1000)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(returnMat)
    ax_title_text = ax.set_title(u'前向逐步回归：迭代次数与回归系数的关系', FontProperties=font)
    ax_xlabel_text = ax.set_xlabel(u'迭代次数', FontProperties=font)
    ax_ylabel_text = ax.set_ylabel(u'回归系数', FontProperties=font)
    plt.setp(ax_title_text, size=15, weight='bold', color='red')
    plt.setp(ax_xlabel_text, size=10, weight='bold', color='black')
    plt.setp(ax_ylabel_text, size=10, weight='bold', color='black')
    plt.show()


if __name__ == '__main__':
    plotstageWiseMat()

from sklearn import linear_model
from bs4 import BeautifulSoup

"""
Desc:
    从页面读取数据，生成retX和retY列表

Parameters:
    retX - 数据X
    retY - 数据Y
    inFile - HTML文件
    yr - 年份
    numPce - 乐高部件数目
    origPrc - 原价
    
Returns:
    None
"""
def scrapePage(retX, retY, inFile, yr, numPce, origPrc):
    # 打开并读取HTML文件
    with open(inFile, encoding='utf-8') as f:
        html = f.read()
    soup = BeautifulSoup(html)
    i = 1
    # 根据HTML页面结构进行解析
    currentRow = soup.find_all('table', r='%d' % i)
    while(len(currentRow) != 0):
        currentRow = soup.find_all('table', r='%d' % i)
        title = currentRow[0].find_all('a')[1].text
        lwrTitle = title.lower()
        # 查找是否有全新标签
        if(lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
            newFlag = 1.0
        else:
            newFlag = 0.0
        # 查找是否已经标志出售，我们只收集已出售的数据
        soldUnicde = currentRow[0].find_all('td')[3].find_all('span')
        if len(soldUnicde) == 0:
            print("商品#%d没有出售" % i)
        else:
            # 解析页面获取当前价格
            soldPrice = currentRow[0].find_all('td')[4]
            priceStr = soldPrice.text
            priceStr = priceStr.replace('$', '')
            priceStr = priceStr.replace(',', '')
            if len(soldPrice) > 1:
                priceStr = priceStr.replace('Free shipping', '')
            sellingPrice = float(priceStr)
            # 去掉不完整的套装价格
            if sellingPrice > origPrc * 0.5:
                print('%d\t%d\t%d\t%f\t%f' % (yr, numPce, newFlag, origPrc, sellingPrice))
                retX.append([yr, numPce, newFlag, origPrc])
                retY.append(sellingPrice)
        i += 1
        currentRow = soup.find_all('table', r='%d' % i)


"""
Desc:
    依次读取六种乐高套装的数据，并生成数据矩阵

Parameters:
    retX - 数据X
    retY - 数据Y
    
Returns:
    None
"""
def setDataCollect(retX, retY):
    # 2006年的乐高8288，部件数目800，原价49.99
    scrapePage(retX, retY, './lego/lego8288.html', 2006, 800, 49.99)
    scrapePage(retX, retY, './lego/lego10030.html', 2002, 3096, 269.99)
    scrapePage(retX, retY, './lego/lego10179.html', 2007, 5195, 499.99)
    scrapePage(retX, retY, './lego/lego10181.html', 2007, 3428, 199.99)
    scrapePage(retX, retY, './lego/lego10189.html', 2008, 5922, 299.99)
    scrapePage(retX, retY, './lego/lego10196.html', 2009, 3263, 249.99)
    

"""
Desc:
    使用sklearn

Parameters:
    None
    
Returns:
    None
"""
def usesklearn():
    reg = linear_model.Ridge(alpha=.5)
    lgX = []
    lgY = []
    setDataCollect(lgX, lgY)
    # fit(X, y):Fit Ridge regression model
    reg.fit(lgX, lgY)
    print("%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价" % (reg.intercept_, reg.coef_[0], reg.coef_[1], reg.coef_[2], reg.coef_[3]))


if __name__ == '__main__':
    usesklearn()