监督学习之四——支持向量机（Support Vector Machines，SVM）

1 支持向量机基本概念（Support Vector Machines，SVM）

1.1 SVM

通常SVM会构造一个或一组距离数据点最大间距（margin）的超平面用于分类、回归和异常值检测，因此SVM也被称作大间距分类器。

对于多元分类，SVM采用ovo（一对一）的方法。

1.2 支持向量和间隔

对于超平面方程${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b=0$，样本空间里任意点$\mathbf{x}$到该超平面的距离为$r=\frac{|{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b|}{||\mathbf{w}||}$，若该超平面能将所有样本都正确分类，则总存在一个平面（缩放变换）使得：
$${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b\ge 1,y_i=1$$

$${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b\le -1,y_i=-1$$

则距离超平面最近的使得上式等号成立的几个训练样本就是支持向量。间隔就是两个异类支持向量到超平面的距离和为$\gamma =\frac{2}{||\mathbf{w}||}$。如下图所示（图片来源《机器学习》周志华）。

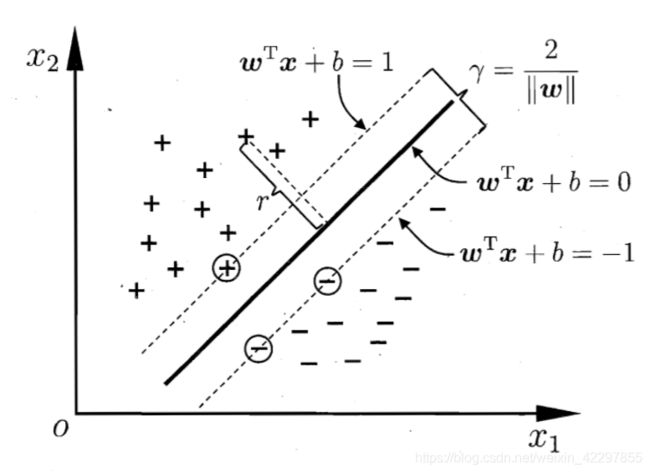
1.3 SVM基本型

根据间隔和支持向量的概念得到基本型（凸二次优化问题）
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$$

$$s.t.y_i({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)\ge 1$$

1.4 对偶问题

利用拉格朗日乘子法得到其对偶问题。

1.5 KKT条件

模型只需记录不为0的${\alpha }_i$，故该式说明最终模型仅跟支持向量有关。

1.6 序列最小最优化（SMO）算法

对于1.4中的对偶问题，这是一个二次规划问题，我们可以利用SMO算法高效算出。

1.7 线性不可分支持向量机与软间隔最大

当样本线性不可分时，我们可以采用核函数用超平面将样本分开，但可能导致过拟合，缓解该问题的方法就是软间隔。具体来说，前面介绍的支持向量机形式是要求所有样本均满足约束$$y_i({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)\ge 1,$$

即所有样本都必须划分正确,这称为“硬间隔”(hardmargin),而软间隔则是允许某些样本不满足该约束。
修改目标函数为
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m\max (0,1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)),$$
在使得间隔最大的同时，还要满足不符合约束的样本尽可能少，其中C>0，这里采用的是“hinge损失函数”

$${\ell }_{\text{hinge}}(z)=\max (0,1-z)$$
引入松弛变量则得到软间隔支持向量机
$$\underset{\mathbf{w},b,{\xi }_i}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\xi }_i$$

$$s.t.y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i$$

$${\xi }_i⩾0,i=1,2,\dots ,m$$

依然使用拉格朗日乘子法得到其对偶问题
$$\begin{array}{rl}\underset{\mathbf{\alpha }}{\max }& \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\\ \text{ s.t. }& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\dots ,m\end{array}$$

可以看出区别就在第二条约束上，同样可以利用SMO算法求解。

2 SVR（Support Vector Regressor）数学原理

数学模型：
$$\underset{w,b,\zeta ,{\zeta }^{\ast }}{\min }\frac{1}{2}{w}^{T}w+C\sum _{i=1}^n({\zeta }_i+{\zeta }_i^{\ast })$$

$$\text{s.t. }{y}_i-w^T\varphi (x_i)-b\le \epsilon +{\zeta }_i,$$

$$w^T\varphi (x_i)+b-y_i\le \epsilon +{\zeta }_i^{\ast },$$

$${\zeta }_i,{\zeta }_i^{\ast }\ge 0,i=1,...,n$$

对偶问题：
$$\underset{\alpha ,{\alpha }^{\ast }}{\min }\frac{1}{2}(\alpha -{\alpha }^{\ast }{)}^T{X}^{T}X(\alpha -{\alpha }^{\ast })+\epsilon e^T(\alpha +{\alpha }^{\ast })-y^T(\alpha -{\alpha }^{\ast })$$

$$\text{s.t. }{e}^T(\alpha -{\alpha }^{\ast })=0,$$

$$0\le {\alpha }_i,{\alpha }_i^{\ast }\le C,i=1,...,n$$

决策函数：
$$\sum _{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })K(x_i,x)+b$$

3 常用kernel函数

线性核函数
$$⟨x,x^{\prime }⟩$$

多项式核函数
$$(\gamma ⟨x,x^{\prime }⟩+r{)}^d$$

rbf
$$\exp (-\gamma \Vert x-x^{\prime }{\Vert }^2),\gamma >0$$

拉普拉斯核
$$\exp (-\frac{||x_i-x_j||}{\sigma }),\sigma >0$$

Sigmoid核函数
$$\tanh (\gamma ⟨x,x^{\prime }⟩+r),\gamma >0,r<0$$

自定义核函数：参考这里