机器学习之简单入门分类算法:KMeans、KNN、Meanshift

大家好呀，我是AI菌，今天和大家分享机器学习里面的简单入门分类算法：KMeans、KNN、Meanshift，话不多说我们进入正题！

KMeans

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

KMeans的介绍大家可能看的一知半解，我们用实战运用一下：
我们引入一个已经标注好的样本，并且可视化

import pandas as pd
import numpy as np
data = pd.read_csv('data.csv')
X = data.drop(['labels'],axis=1)
y = data.loc[:,'labels']
fig1 = plt.figure()
label0 = plt.scatter(X.loc[:,'V1'][y==0],X.loc[:,'V2'][y==0])
label1 = plt.scatter(X.loc[:,'V1'][y==1],X.loc[:,'V2'][y==1])
label2 = plt.scatter(X.loc[:,'V1'][y==2],X.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

运用KMeans模型

from sklearn.cluster import KMeans
KM = KMeans(n_clusters3,random_state=0 #c_clusters为分成若干类，random可理解成每个类随机标签
KM.fit(X)#模型训练
center = KM.cluster_center_#显示训练后的中心点
print(center)

结果：array([[ 40.68362784, 59.71589274],[ 69.92418447, -10.11964119], [ 9.4780459 , 10.686052 ]])
我们把中心点在上图可视化，如下：

模型训练完成后，要进行模型的预测以及预测结果可视化：

y_predict = KM.predict(X)
#visualize the data and results
fig4 = plt.subplot(121)
label0 = plt.scatter(X.loc[:,'V1'][y_predict==0],X.loc[:,'V2'][y_predict==0])
label1 = plt.scatter(X.loc[:,'V1'][y_predict==1],X.loc[:,'V2'][y_predict==1])
label2 = plt.scatter(X.loc[:,'V1'][y_predict==2],X.loc[:,'V2'][y_predict==2])

plt.title("predicted data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])

对比发现，预测结果和实际结果大致相同，但因为是无监督学习，每个类的标签不一样，所以和实际结果的标签有误，最后进行结果矫正：

y_corrected = []
for i in y_predict:
    if i==0:
        y_corrected.append(2)
    elif i==2:
        y_corrected.append(0)
    else:
        y_corrected.append(1)

最后用y_corrected为标签进行可视化，就完成矫正啦~~而且准确率为0.997

Meanshift

Mean Shift算法的关键操作是通过感兴趣区域内的数据密度变化计算中心点的漂移向量，从而移动中心点进行下一次迭代，直到到达密度最大处（中心点不变）。从每个数据点出发都可以进行该操作，在这个过程，统计出现在感兴趣区域内的数据的次数。该参数将在最后作为分类的依据。
与K-Means算法不一样的是，Mean Shift算法可以自动决定类别的数目。与K-Means算法一样的是，两者都用集合内数据点的均值进行中心点的移动。
下图为MeanShitf的流程图：

实战环节：

from sklearn.cluster import MeanShift,estimate_bandwidth
bw = estimate_bandwidth(X,n_samples=500)#X为原始数据集，n_samples为取若干的点进行估计带宽（半径）
#estimate_bandwidth函数用作于mean-shift算法估计带宽，如果MeanShift函数没有传入bandwidth参数，MeanShift会自动运行estimate_bandwidth
ms = MeanShift(bandwidth=bw)
ms.fit(X)
y_predict_ms = ms.predict(X)
#最后直接进行可视化
fig6 = plt.subplot(121)
label0 = plt.scatter(X.loc[:,'V1'][y_predict_ms==0],X.loc[:,'V2'][y_predict_ms==0])
label1 = plt.scatter(X.loc[:,'V1'][y_predict_ms==1],X.loc[:,'V2'][y_predict_ms==1])
label2 = plt.scatter(X.loc[:,'V1'][y_predict_ms==2],X.loc[:,'V2'][y_predict_ms==2])

plt.title("ms results")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])
plt.show()

因为MeanShift为非监督学习，所以最后标签有可能和原始标签不合，我们要进行结果矫正，方法和KMeans基本相同，就不展示啦~~

knn的话，下期手撸knn源码和大家分享！！

拓展

K-means算法是将样本聚类成k个簇（cluster），具体算法描述如下：
1、 随机选取k个聚类质心点（cluster centroids）为
2、 重复下面过程直到收敛 :
对于每一个样例i，计算其应该属于的类

对于每一个类j，重新计算该类的质心

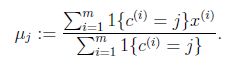
K是我们事先给定的聚类数，Cⁱ代表样例i与k个类中距离最近的那个类，Cⁱ的值是1到k中的一个。质心μⁱ代表我们对属于同一个类的样本中心点的猜测.