机器学习系列26-循环神经网络(Ⅰ)
Recurrent Neural Network(Ⅰ)
RNN,或者说最常用的LSTM,一般用于记住之前的状态,以供后续神经网络的判断,它由input gate、forget gate、output gate和cell memory组成,每个LSTM本质上就是一个neuron,特殊之处在于有4个输入: z z z和三门控制信号 z i z_i zi、 z f z_f zf和 z o z_o zo,每个时间点的输入都是由当前输入值+上一个时间点的输出值+上一个时间点cell值来组成
Introduction
Slot Filling
在智能客服、智能订票系统中,往往会需要slot filling技术,它会分析用户说出的语句,将时间、地址等有效的关键词填到对应的槽上,并过滤掉无效的词语
词汇要转化成vector,可以使用1-of-N编码,word hashing或者是word vector等方式,此外我们可以尝试使用Feedforward Neural Network来分析词汇,判断出它是属于时间或是目的地的概率
但这样做会有一个问题,该神经网络会先处理“arrive”和“leave”这两个词汇,然后再处理“Taipei”,这时对NN来说,输入是相同的,它没有办法区分出“Taipei”是出发地还是目的地
这个时候我们就希望神经网络是有记忆的,如果NN在看到“Taipei”的时候,还能记住之前已经看过的“arrive”或是“leave”,就可以根据上下文得到正确的答案

这种有记忆力的神经网络,就叫做Recurrent Neural Network(RNN)
在RNN中,hidden layer每次产生的output a 1 a_1 a1、 a 2 a_2 a2,都会被存到memory里,下一次有input的时候,这些neuron就不仅会考虑新输入的 x 1 x_1 x1、 x 2 x_2 x2,还会考虑存放在memory中的 a 1 a_1 a1、 a 2 a_2 a2
注:在input之前,要先给内存里的 a i a_i ai赋初始值,比如0

注意到,每次NN的输出都要考虑memory中存储的临时值,而不同的输入产生的临时值也尽不相同,因此改变输入序列的顺序会导致最终输出结果的改变(Changing the sequence order will change the output)
Slot Filling with RNN
用RNN处理Slot Filling的流程举例如下:
- “arrive”的vector作为 x 1 x^1 x1输入RNN,通过hidden layer生成 a 1 a^1 a1,再根据 a 1 a^1 a1生成 y 1 y^1 y1,表示“arrive”属于每个slot的概率,其中 a 1 a^1 a1会被存储到memory中
- “Taipei”的vector作为 x 2 x^2 x2输入RNN,此时hidden layer同时考虑 x 2 x^2 x2和存放在memory中的 a 1 a^1 a1,生成 a 2 a^2 a2,再根据 a 2 a^2 a2生成 y 2 y^2 y2,表示“Taipei”属于某个slot的概率,此时再把 a 2 a^2 a2存到memory中
- 依次类推

注意:上图为同一个RNN在三个不同时间点被分别使用了三次,并非是三个不同的NN
这个时候,即使输入同样是“Taipei”,我们依旧可以根据前文的“leave”或“arrive”来得到不一样的输出

Elman Network & Jordan Network
RNN有不同的变形:
- Elman Network:将hidden layer的输出保存在memory里
- Jordan Network:将整个neural network的输出保存在memory里
由于hidden layer没有明确的训练目标,而整个NN具有明确的目标,因此Jordan Network的表现会更好一些

Bidirectional RNN
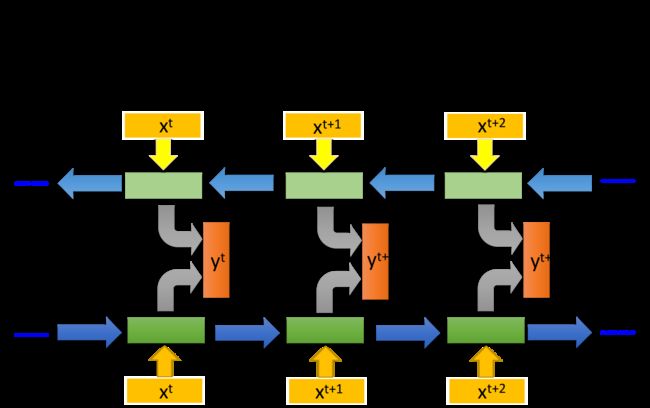
RNN 还可以是双向的,你可以同时训练一对正向和反向的RNN,把它们对应的hidden layer x t x^t xt拿出来,都接给一个output layer,得到最后的 y t y^t yt
使用Bi-RNN的好处是,NN在产生输出的时候,它能够看到的范围是比较广的,RNN在产生 y t + 1 y^{t+1} yt+1的时候,它不只看了从句首 x 1 x^1 x1开始到 x t + 1 x^{t+1} xt+1的输入,还看了从句尾 x n x^n xn一直到 x t + 1 x^{t+1} xt+1的输入,这就相当于RNN在看了整个句子之后,才决定每个词汇具体要被分配到哪一个槽中,这会比只看句子的前一半要更好
LSTM
前文提到的RNN只是最简单的版本,并没有对memory的管理多加约束,可以随时进行读取,而现在常用的memory管理方式叫做长短期记忆(Long Short-term Memory),简称LSTM
冷知识:可以被理解为比较长的短期记忆,因此是short-term,而非是long-short term
Three-gate
LSTM有三个gate:
-
当某个neuron的输出想要被写进memory cell,它就必须要先经过一道叫做input gate的闸门,如果input gate关闭,则任何内容都无法被写入,而关闭与否、什么时候关闭,都是由神经网络自己学习到的
-
output gate决定了外界是否可以从memory cell中读取值,当output gate关闭的时候,memory里面的内容同样无法被读取
-
forget gate则决定了什么时候需要把memory cell里存放的内容忘记清空,什么时候依旧保存

整个LSTM可以看做是4个input,1个output:
- 4个input=想要被存到memory cell里的值+操控input gate的信号+操控output gate的信号+操控forget gate的信号
- 1个output=想要从memory cell中被读取的值
Memory Cell
如果从表达式的角度看LSTM,它比较像下图中的样子
- z z z是想要被存到cell里的输入值
- z i z_i zi是操控input gate的信号
- z o z_o zo是操控output gate的信号
- z f z_f zf是操控forget gate的信号
- a a a是综合上述4个input得到的output值
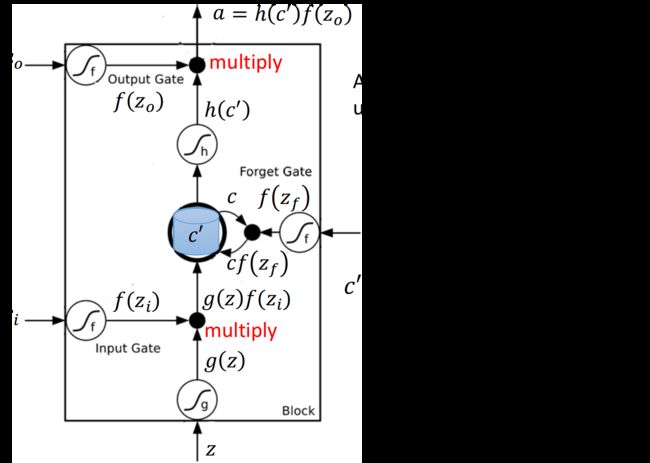
把 z z z、 z i z_i zi、 z o z_o zo、 z f z_f zf通过activation function,分别得到 g ( z ) g(z) g(z)、 f ( z i ) f(z_i) f(zi)、 f ( z o ) f(z_o) f(zo)、 f ( z f ) f(z_f) f(zf)
其中对 z i z_i zi、 z o z_o zo和 z f z_f zf来说,它们通过的激活函数 f ( ) f() f()一般会选sigmoid function,因为它的输出在0~1之间,代表gate被打开的程度
令 g ( z ) g(z) g(z)与 f ( z i ) f(z_i) f(zi)相乘得到 g ( z ) ⋅ f ( z i ) g(z)\cdot f(z_i) g(z)⋅f(zi),然后把原先存放在cell中的 c c c与 f ( z f ) f(z_f) f(zf)相乘得到 c f ( z f ) cf(z_f) cf(zf),两者相加得到存在memory中的新值 c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) c'=g(z)\cdot f(z_i)+cf(z_f) c′=g(z)⋅f(zi)+cf(zf)
- 若 f ( z i ) = 0 f(z_i)=0 f(zi)=0,则相当于没有输入,若 f ( z i ) = 1 f(z_i)=1 f(zi)=1,则相当于直接输入 g ( z ) g(z) g(z)
- 若 f ( z f ) = 1 f(z_f)=1 f(zf)=1,则保存原来的值 c c c并加到新的值上,若 f ( z f ) = 0 f(z_f)=0 f(zf)=0,则旧的值将被遗忘清除
从中也可以看出,forget gate的逻辑与我们的直觉是相反的,控制信号打开表示记得,关闭表示遗忘
此后, c ′ c' c′通过激活函数得到 h ( c ′ ) h(c') h(c′),与output gate的 f ( z o ) f(z_o) f(zo)相乘,得到输出 a = h ( c ′ ) f ( z o ) a=h(c')f(z_o) a=h(c′)f(zo)
LSTM Example
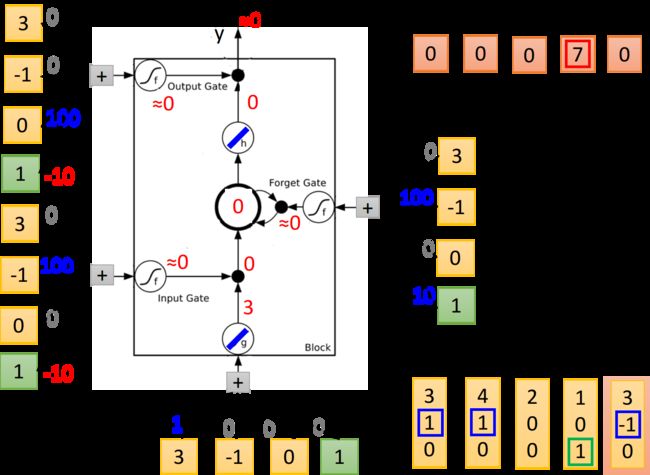
下图演示了一个LSTM的基本过程, x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3是输入序列, y y y是输出序列,基本原则是:
- 当 x 2 = 1 x_2=1 x2=1时,将 x 1 x_1 x1的值写入memory
- 当 x 2 = − 1 x_2=-1 x2=−1时,将memory里的值清零
- 当 x 3 = 1 x_3=1 x3=1时,将memory里的值输出
- 当neuron的输入为正时,对应gate打开,反之则关闭
LSTM Structure
你可能会觉得上面的结构与平常所见的神经网络不太一样,实际上我们只需要把LSTM整体看做是下面的一个neuron即可

假设目前我们的hidden layer只有两个neuron,则结构如下图所示:
- 输入 x 1 x_1 x1、 x 2 x_2 x2会分别乘上四组不同的weight,作为neuron的输入以及三个状态门的控制信号
- 在原来的neuron里,1个input对应1个output,而在LSTM里,4个input才产生1个output,并且所有的input都是不相同的
- 从中也可以看出LSTM所需要的参数量是一般NN的4倍

LSTM for RNN
从上图中你可能看不出LSTM与RNN有什么关系,接下来我们用另外的图来表示它
假设我们现在有一整排的LSTM作为neuron,每个LSTM的cell里都存了一个scalar值,把所有的scalar连接起来就组成了一个vector c t − 1 c^{t-1} ct−1
在时间点 t t t,输入了一个vector x t x^t xt,它会乘上一个matrix,通过转换得到 z z z,而 z z z的每个dimension就代表了操控每个LSTM的输入值,同理经过不同的转换得到 z i z^i zi、 z f z^f zf和 z o z^o zo,得到操控每个LSTM的门信号

下图是单个LSTM的运算情景,其中LSTM的4个input分别是 z z z、 z i z^i zi、 z f z^f zf和 z o z^o zo的其中1维,每个LSTM的cell所得到的input都是各不相同的,但它们却是可以一起共同运算的,整个运算流程如下图左侧所示:
f ( z f ) f(z^f) f(zf)与上一个时间点的cell值 c t − 1 c^{t-1} ct−1相乘,并加到经过input gate的输入 g ( z ) ⋅ f ( z i ) g(z)\cdot f(z^i) g(z)⋅f(zi)上,得到这个时刻cell中的值 c t c^t ct,最终再乘上output gate的信号 f ( z o ) f(z^o) f(zo),得到输出 y t y^t yt

上述的过程反复进行下去,就得到下图中各个时间点上,LSTM值的变化情况,其中与上面的描述略有不同的是,这里还需要把hidden layer的最终输出 y t y^t yt以及当前cell的值 c t c^t ct都连接到下一个时间点的输入上
因此在下一个时间点操控这些gate值,不只是看输入的 x t + 1 x^{t+1} xt+1,还要看前一个时间点的输出 h t h^t ht和cell值 c t c^t ct,你需要把 x t + 1 x^{t+1} xt+1、 h t h^t ht和 c t c^t ct这3个vector并在一起,乘上4个不同的转换矩阵,去得到LSTM的4个输入值 z z z、 z i z^i zi、 z f z^f zf、 z o z^o zo,再去对LSTM进行操控
注意:下图是同一个LSTM在两个相邻时间点上的情况

上图是单个LSTM作为neuron的情况,事实上LSTM基本上都会叠多层,如下图所示,左边两个LSTM代表了两层叠加,右边两个则是它们在下一个时间点的状态
