主席树（区间查询第k小数+单点修改）HDU2665

主席树

【引入】

学习推荐博客（内有带修改的博文链接）：https://www.cnblogs.com/Empress/p/4652449.html

主席树可以干什么？

主席树可以求一个序列某区间段的第k小数。（时间复杂度O(m*logn）m是询问次数。);

学习主席树之前必须掌握线段树，主席树是建立在线段树的基础上的。

【算法】

线段树可以维护区间和、最值。这里我们用的是维护和，维护谁的和呢？

维护原序列中的数据在区间[l,r]内的数字个数！这里的l r指的是数值大小！

设给出的序列是数组a[]={2,8,5,1,5}，总区间[L,R]=[1,5]，即5个数，这里的L，R指的是a的下标！

不妨我们先拿总区间[1,5]来说，对这个总区间建立一棵线段树，维护数据区间[l,r]之间数字个数，这里l，r应该取序列a的最小值1和最大值8。若题目给的数太大，一般要进行离散化，下文再提。

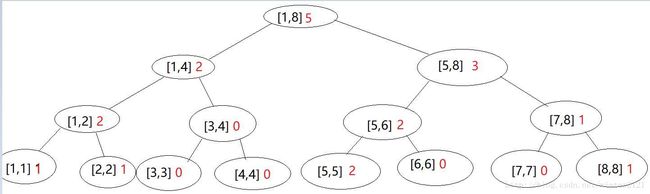
画出这棵线段树：

红色数字代表出现在数据区间[l,r]内的数字个数。

现在有了这棵线段树，我就能询问总区间【1,5】内的第k小数了。比如k=2，走一波~，令p=[1,8](根结点)

p为根结点区间内有5个数，左孩子有2个数，那么目标值一定在左子树，进入左树。p=[1,4]

p的左孩子有2个数，故还是要进入左子树。p=[1,2]

p的左孩子有1个，k大于左孩子，故p要进入右孩子。p=[2,2]

到达叶子结点，访问完毕，此叶子即为目标值——第k小数

1、现在我们会询问总区间【L，R】的第k小数了，那么对任意区间怎么维护呢？

答：建立n棵这样的线段树，第i棵维护 序列区间【1，i】，上面画的那棵维护的就是【1，n】；

2、得到n棵线段树，然后不就只能询问左端点为1的线段树吗？怎么询问【l，r】？

答：树相减。还记得数列前n项和Sn吗，若我求【L,R】之间的和S'，不就是S' = S(R) - R(L-1)吗。类比到这里的n棵线段树，求【L,R】时，直接让第R棵减掉第L-1棵树，得到的树，再寻找目标值即可！相减原则：两棵树一定是长得一模一样的，按照相同位置相减即可！

3、建立n棵线段树，内存承受得了吗？

答：肯定爆内存。怎么办？我们在构造第 i 棵线段树的时候，实际上就是把第 i-1 棵数复制过来，然后把第 i 个数字加入进去，只会修改一个从根到一个叶子的路径，修改的结点数就是log(n)+1个。现实就是第 i 棵树，同第 i-1 棵树相同的结点，不再为i树申请空间，直接让其对应位置的孩子指针指向第i-1棵树的对应结点，即结点公用

处理完这三个问题，空间复杂度O(n*logN)，单次询问的时间复杂度O(log N)

上面遗留了一个问题：数据太大怎么办？离散化。比如上面那个数列a[]={2,8,5,1,5}，离散化之后是{2,4,3,1,3}。其实就是把数字之间的差降到最低，但不改变原序列大小关系。

【例题HDU2665】

题意说的是求第k大数，我觉得我交的代码是求第k小数。。我认为的是{1,2,3}的第1大数是3,而这个题要输出1才对。

【代码】

#include
using namespace std;
const int MAX=201000;
int sum[MAX<<5],T[MAX],L[MAX<<5],R[MAX<<5],cnt; //数量,根.左.右孩子指针,结点计数//至少d+d*logd=d<<4
int cas,n,m;
int a[MAX],ha[MAX]; //原序列，离散化
int build(int l,int r) //初始线段树,[l,r]为离散数字区间
{
    int rt=++cnt;
    sum[rt]=0;
    if(l>1;
        L[rt]=build(l,mid);
        R[rt]=build(mid+1,r);
    }
    return rt;
}
int update(int u,int x,int l,int r)  //离散数字x加入u树,返回新树
{
    int rt=++cnt;//新结点
    sum[rt]=sum[u]+1; L[rt]=L[u]; R[rt]=R[u];
    if(l>1;
        if(x<=mid)
            L[rt]=update(L[u],x,l,mid);
        else
            R[rt]=update(R[u],x,mid+1,r);
    }
    return rt;  //返回当前地址
}
int query(int u,int v,int k,int l,int r) //u树-v树得第k小数
{
    if(l==r)return r;
    int s=sum[L[u]]-sum[L[v]]; //左孩子sum
    int mid=(l+r)>>1;
    if(k<=s)
        return query(L[u],L[v],k,l,mid); //在左树
    else return query(R[u],R[v],k-s,mid+1,r);
}
int main()
{
    scanf("%d",&cas);
    while(cas--)
    {
        cnt=1;  //至关重要！
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]),ha[i]=a[i];
        sort(ha+1,ha+n+1);  //预处理排序
        int N=unique(ha+1,ha+1+n)-ha-1; //离散化
        T[0]=build(1,N);
        for(int i=1;i<=n;i++)  //加入数字
        {
            int x=lower_bound(ha+1,ha+1+N,a[i])-ha; //a[i]第x小
            T[i]=update(T[i-1],x,1,N); //[1,N]是ha范围,加入x
        }
        while(m--)
        {
            int x,y,k;
            scanf("%d%d%d",&x,&y,&k);
            //k=r-k+l;  //可求第k大数
            int ans=query(T[y],T[x-1],k,1,N);  //query[l,r]
            printf("%d\n",ha[ans]);//别忘了离散化
        }
    }
}

【能修改的主席树】树状数组维护主席树

#include 
using namespace std;
#define lson l, m
#define rson m+1, r
const int N=60005;
int T[N], L[N<<5], R[N<<5], sum[N<<5];
int S[N], use1[N],use2[N];
int n, m, tot;
int a[N], Hash[N];
struct node
{
    int l, r, k;
    bool Q;
}op[10005];
int build(int l, int r)
{
    int rt=(++tot);
    sum[rt]=0;
    if(l>1;
        L[rt]=build(lson);
        R[rt]=build(rson);
    }
    return rt;
}
int update(int pre, int l, int r, int x, int val)
{
    int rt=(++tot);
    L[rt]=L[pre], R[rt]=R[pre], sum[rt]=sum[pre]+val;
    if(l>1;
        if(x<=m)
            L[rt]=update(L[pre], lson, x, val);
        else
            R[rt]=update(R[pre], rson, x, val);
    }
    return rt;
}
void add(int x, int p, int d)
{
    for(;x<=n;x+=x&-x)
        S[x]=update(S[x], 1, m, p, d);
}
int Sum(int x,int *use)
{
    int ret=0;
    for(;x;x-=x&-x)
        ret+=sum[L[use[x]]];
    return ret;
}
int query(int u, int v, int lr, int rr, int l, int r, int k)
{
    if(l>=r)
        return l;
    int m=(l+r)>>1;
    int tmp=Sum(v,use2)-Sum(u,use1)+sum[L[rr]]-sum[L[lr]];
    if(tmp>=k)
    {
        for(int i=u;i;i-=i&-i)
            use1[i]=L[use1[i]];
        for(int i=v;i;i-=i&-i)
            use2[i]=L[use2[i]];
        return query(u, v, L[lr], L[rr], lson, k);
    }
    else
    {
        for(int i=u;i;i-=i&-i)
            use1[i]=R[use1[i]];
        for(int i=v;i;i-=i&-i)
            use2[i]=R[use2[i]];
        return query(u, v, R[lr], R[rr], rson, k-tmp);
    }
}
int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        int q;
        scanf("%d%d", &n, &q);
        tot=0;
        m=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d", &a[i]);
            Hash[++m]=a[i];
        }
        for(int i=0;i