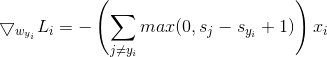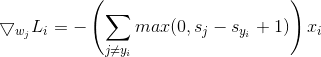CS231n作业（二）SVM分类

一、作业说明

CS231n的第二次作业，要求写一个基于svm的多分类程序，实现cifar10的多分类功能，程序中应当体现损失函数计算、梯度计算、交叉验证选择参数、权重可视化等功能。

二、背景知识

损失函数

                                                      

损失函数分为两部分，前半部分的误差项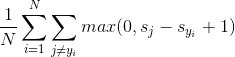和后半部分的正则项。前半部分的误差由正确类别的socre减去模型对每一类别输出的socre和一个“boundary”(这里设为1)得到。后半部分的正则项提升了模型的泛化性能，是正则项系数，本模型中，我们选用的是权重矩阵的F范数。

梯度计算

我们使用分析梯度计算方法。对于属于第类的输入样本，不考虑正则项，模型的loss关于W求梯度为

若为的F范数，

超参数选择

模型中的超参数有两个。一个是正则项系数，一个是学习率learning rate。为确定两个参数合适的取值，我们使用交叉验证法。

权重可视化

计算socre的过程中，权重矩阵W的每一行与输入的特征向量做卷积。考虑到特征向量是由输入图片拉伸得到的。我们可以认为权重矩阵的每一行也是由一张图片拉伸得到的。通过对权重矩阵每一行做可视化，我们可以观察到权重矩阵的部分性质。

三、程序源码

# -*- coding: utf-8 -*-
"""
Created on Sat Oct 13 09:52:31 2018

@author: wjp_ctt
"""

import numpy as np
import random
from matplotlib import pylab as plt


#读取cifar10数据
def unpickle(file):
    import pickle
    with open(file, 'rb') as fo:
        dict = pickle.load(fo, encoding='bytes')
    return dict

def sample_training_data(data, labels, num):
        batch_index= np.random.randint(0, data.shape[0], num)
        batch=data[batch_index].T
        batch_labels=labels[batch_index]
        return batch, batch_labels

def get_validation_set(k_fold, num_validation, training_data):
    num_training=np.size(training_data, 0)
    validation_set=random.sample(range(0,num_training),k_fold*num_validation)
    validation_set=np.reshape(validation_set,[num_validation, k_fold])
    return validation_set

#进行数据预处理（归一化并加上偏置）
def preprocessing(data):
    mean=np.mean(data,axis=0)
    std=np.std(data,axis=0)
    data=np.subtract(data,mean)
    data=np.divide(data, std)
    data=np.hstack([data, np.ones((data.shape[0],1))])
    return data

#定义svm损失函数    
def svm_loss_gradient(w, x, y, alpha):
    socre=np.dot(w, x)
    loss=socre-np.diagonal(socre[y.T])+1
    loss[loss<=0]=0
    loss_sum=np.sum(loss, axis=0)-1
    total_loss=np.sum(loss_sum)/(x.shape[1])+0.5*alpha*np.linalg.norm(w)
  
    w_gradient=np.zeros_like(w)
    for index in range(0, x.shape[1]):
        gradient_temp=np.outer(loss[:,index], x[:,index])
        gradient_temp[y[index],:]=-loss_sum[index]*x[:,index]
        w_gradient+=gradient_temp
    
    #加入正则化项
    w_gradient/=x.shape[1]
    w_gradient+=alpha*w
    return total_loss, w_gradient
   
#跟新权重矩阵
def update(w_gradient, w, learning_rate):
    w += -learning_rate*w_gradient
    return w

#训练函数
def training(info, num_batches, steps, learning_rate, alpha, training_data, training_labels):
    w=np.random.uniform(-0.1, 0.1,(10, training_data.shape[1]))
    loss=np.zeros(steps)
    for inter in range(steps):
        batch, batch_labels=sample_training_data(training_data, training_labels, num_batches) 
        total_loss, gradient=svm_loss_gradient(w, batch, batch_labels, alpha)
        loss[inter]=total_loss
        update(gradient, w, learning_rate)
        if info==1:
            if np.mod(inter, 50)==0:        
                print('Steps ',inter,' finished. Loss is ', total_loss,' \n')
                plt.figure(0)
                plt.plot(range(steps), loss)
                plt.xlabel('iteration times')
                plt.ylabel('loss')
                plt.savefig('Loss')    
    return w

#测试函数
def testing(w, testing_data, testing_labels):
    socre=np.dot(w, testing_data.T)    
    result=np.argmax(socre,axis=0)
    correct=np.where(result==testing_labels) 
    correct_num=np.size(correct[0])
    accuracy=correct_num/testing_data.shape[0]
    return accuracy

#可视化函数
def visualization(w):
    w_no_bias=w[:,:-1]
    w_reshape=np.reshape(w_no_bias,  [-1,3,32,32])
    w_reshape=w_reshape.transpose((0,2,3,1))
    classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
    for i in range(10):
        w_min=np.min(w_reshape[i,:,:,:])
        w_max=np.max(w_reshape[i,:,:,:])
        w_image=255*(w_reshape[i,:,:,:].squeeze()-w_min)/(w_max-w_min)
        plt.figure(i+1)
        plt.imshow(w_image.astype(np.uint8))
        plt.title(classes[i])
        plt.axis('off')
        image_name=str(i)+'.png'
        plt.savefig(image_name)    

#构建训练数据集
training_data=np.zeros([50000,3072],dtype=np.uint8)
training_filenames=np.zeros([50000],dtype=list)
training_labels=np.zeros([50000],dtype=np.int)
for i in range(0,5):
    file_name='cifar-10-python/cifar-10-batches-py/data_batch_'+str(i+1)
    temp=unpickle(file_name)
    training_data[i*10000+0:i*10000+10000,:]=temp.get(b'data')
    training_filenames[i*10000+0:i*10000+10000]=temp.get(b'filenames')
    training_labels[i*10000+0:i*10000+10000]=temp.get(b'labels')
print('Training data loaded: 50000 samples from 10 categories!\n')

#构建测试数据集
testing_data=np.zeros([10000,3072],dtype=np.uint8)
testing_filenames=np.zeros([10000],dtype=list)
testing_labels=np.zeros([10000],dtype=np.int)
file_name='cifar-10-python/cifar-10-batches-py/test_batch'
temp=unpickle(file_name)
testing_data=temp.get(b'data')
testing_filenames=temp.get(b'filenames')
testing_labels=temp.get(b'labels')
print('Testing data loaded: 10000 samples from 10 categories!\n')

#预处理
training_data=preprocessing(training_data)
testing_data=preprocessing(testing_data)

#从训练集中随机采样出测试集
k_fold=5
num_validation=1000
validation_set=get_validation_set(k_fold, num_validation, training_data)
print('Validation data created from training data: %d folds and %d samples for each fold.\n '%(k_fold, num_validation))

#超参数候选范围
learning_rate_candidate=[1e-2, 5e-3, 1e-3, 5e-4, 1e-4, 5e-5, 1e-5]
alpha_candidate=[0.1, 0.5, 1, 5, 10, 20]


#进行k-fold交叉验证
validation_accuracy=np.zeros([len(learning_rate_candidate),len(alpha_candidate), k_fold])
for i, learning_rate in enumerate(learning_rate_candidate):
    for j, alpha in enumerate(alpha_candidate):
        for k in range(k_fold):
            validation_training=np.delete(validation_set,0,axis=1)
            validation_training=np.reshape(validation_training,[(k_fold-1)*num_validation])
            validation_training_labels=training_labels[validation_training]
            validation_training=training_data[validation_training,:]
            validation_testing=training_data[validation_set[:,k],:]
            validation_testing_labels=training_labels[validation_set[:,k]]
            w=training(0, 32, 500, learning_rate, alpha, validation_training, validation_training_labels)
            accuracy=testing(w, validation_testing, validation_testing_labels)
            validation_accuracy[i][j][k]=accuracy
        print('learning rate %e alpha %e accuracy: %f' % (learning_rate, alpha, np.mean(validation_accuracy[i][j][:])))
par =np.where(np.mean(validation_accuracy,2)==np.max(np.mean(validation_accuracy,2)))           
learning_rate=learning_rate_candidate[int(par[0])]
alpha=alpha_candidate[int(par[1])]
print('The chosen parameters: learning rate %e alpha %f'% (learning_rate, alpha))

#训练过程
print('Training...\n')
num_batches=128
steps=1500
info=1
w=training(1, num_batches, steps, learning_rate, alpha, training_data, training_labels)
   
#测试阶段
print('Testing...\n')
accuracy=testing(w, testing_data, testing_labels)
print('accuracy is ',accuracy)

#可视化权重矩阵
visualization(w)

四、程序输出

样本读取

Training data loaded: 50000 samples from 10 categories!

Testing data loaded: 10000 samples from 10 categories!

Validation data created from training data: 5 folds and 1000 samples for each fold.

交叉验证

learning rate 1.000000e-02 alpha 1.000000e-01 accuracy: 0.093600
learning rate 1.000000e-02 alpha 5.000000e-01 accuracy: 0.093600
learning rate 1.000000e-02 alpha 1.000000e+00 accuracy: 0.093600
learning rate 1.000000e-02 alpha 5.000000e+00 accuracy: 0.093600
learning rate 1.000000e-02 alpha 1.000000e+01 accuracy: 0.093600
learning rate 1.000000e-02 alpha 2.000000e+01 accuracy: 0.093600
learning rate 5.000000e-03 alpha 1.000000e-01 accuracy: 0.145800
learning rate 5.000000e-03 alpha 5.000000e-01 accuracy: 0.132000
learning rate 5.000000e-03 alpha 1.000000e+00 accuracy: 0.132000
learning rate 5.000000e-03 alpha 5.000000e+00 accuracy: 0.111200
learning rate 5.000000e-03 alpha 1.000000e+01 accuracy: 0.118400
learning rate 5.000000e-03 alpha 2.000000e+01 accuracy: 0.134400
learning rate 1.000000e-03 alpha 1.000000e-01 accuracy: 0.309200
learning rate 1.000000e-03 alpha 5.000000e-01 accuracy: 0.310400
learning rate 1.000000e-03 alpha 1.000000e+00 accuracy: 0.315600
learning rate 1.000000e-03 alpha 5.000000e+00 accuracy: 0.299000
learning rate 1.000000e-03 alpha 1.000000e+01 accuracy: 0.275400
learning rate 1.000000e-03 alpha 2.000000e+01 accuracy: 0.244200
learning rate 5.000000e-04 alpha 1.000000e-01 accuracy: 0.280600
learning rate 5.000000e-04 alpha 5.000000e-01 accuracy: 0.290400
learning rate 5.000000e-04 alpha 1.000000e+00 accuracy: 0.289200
learning rate 5.000000e-04 alpha 5.000000e+00 accuracy: 0.330600
learning rate 5.000000e-04 alpha 1.000000e+01 accuracy: 0.345800
learning rate 5.000000e-04 alpha 2.000000e+01 accuracy: 0.322200
learning rate 1.000000e-04 alpha 1.000000e-01 accuracy: 0.215000
learning rate 1.000000e-04 alpha 5.000000e-01 accuracy: 0.223400
learning rate 1.000000e-04 alpha 1.000000e+00 accuracy: 0.221000
learning rate 1.000000e-04 alpha 5.000000e+00 accuracy: 0.225800
learning rate 1.000000e-04 alpha 1.000000e+01 accuracy: 0.239400
learning rate 1.000000e-04 alpha 2.000000e+01 accuracy: 0.257200
learning rate 5.000000e-05 alpha 1.000000e-01 accuracy: 0.201800
learning rate 5.000000e-05 alpha 5.000000e-01 accuracy: 0.208200
learning rate 5.000000e-05 alpha 1.000000e+00 accuracy: 0.205800
learning rate 5.000000e-05 alpha 5.000000e+00 accuracy: 0.202600
learning rate 5.000000e-05 alpha 1.000000e+01 accuracy: 0.195200
learning rate 5.000000e-05 alpha 2.000000e+01 accuracy: 0.219200
learning rate 1.000000e-05 alpha 1.000000e-01 accuracy: 0.158200
learning rate 1.000000e-05 alpha 5.000000e-01 accuracy: 0.161600
learning rate 1.000000e-05 alpha 1.000000e+00 accuracy: 0.163800
learning rate 1.000000e-05 alpha 5.000000e+00 accuracy: 0.161600
learning rate 1.000000e-05 alpha 1.000000e+01 accuracy: 0.154800
learning rate 1.000000e-05 alpha 2.000000e+01 accuracy: 0.158200
The chosen parameters: learning rate 5.000000e-04 alpha 10.000000

训练

Training...

Steps  0  finished. Loss is  71.11918025110381  

Steps  50  finished. Loss is  46.643721521245716  

Steps  100  finished. Loss is  37.364724105652755  

Steps  150  finished. Loss is  30.191387606120355  

Steps  200  finished. Loss is  24.176320343657533  

Steps  250  finished. Loss is  19.718968439649625  

Steps  300  finished. Loss is  16.595082508625858  

Steps  350  finished. Loss is  14.743217478486436  

Steps  400  finished. Loss is  11.937510142621218  

Steps  450  finished. Loss is  10.71235519377327  

Steps  500  finished. Loss is  9.430591275017388  

Steps  550  finished. Loss is  9.081815266374942  

Steps  600  finished. Loss is  8.2660485434116  

Steps  650  finished. Loss is  7.887563196133932  

Steps  700  finished. Loss is  7.556880215944423  

Steps  750  finished. Loss is  7.221866257724002  

Steps  800  finished. Loss is  7.3146908997620015  

Steps  850  finished. Loss is  7.0765671744413625  

Steps  900  finished. Loss is  6.843564906997641  

Steps  950  finished. Loss is  6.40988618924709  

Steps  1000  finished. Loss is  6.150195888710124  

Steps  1050  finished. Loss is  6.817769717732817  

Steps  1100  finished. Loss is  6.130373543128535  

Steps  1150  finished. Loss is  6.311755927599913  

Steps  1200  finished. Loss is  6.458824853519376  

Steps  1250  finished. Loss is  6.481816340503165  

Steps  1300  finished. Loss is  6.699008213895308  

Steps  1350  finished. Loss is  6.187601219274654  

Steps  1400  finished. Loss is  7.046172999028601  

Steps  1450  finished. Loss is  6.7576505777703515  

测试及结果

Testing...

accuracy is  0.3544

五、结果说明

经过交叉验证，最优正则化系数和学习率的值为10和0.0005。在训练过程中损失函数值不断下降。最终模型在10000张图片上的测试结果为35.44%。考虑到我们是直接基于像素特征进行训练的，这个结果可以接受。可以通过提取比像素特征更一般的特征提升测试结果。

模型的可视化结果。下图是青蛙的权重可视化结果。我们看到，中间的部分有集中的绿色，这也符合青蛙是绿色的常识。