数据结构与算法简记：通过前序中序或中序后序构建二叉树

上次记录了广义表生成二叉树的过程，我们也可以通过前序和中序，或者中序和后序，来确定和构建一棵唯一的二叉树。

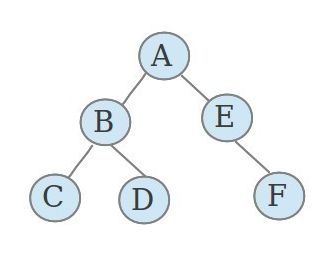
还是同样的图，它的前序，中序，后序遍历序列分别是：

pre: ABCDEF
in: CBDAEF
post: CDBFEA

以下是通过前序和中序构建二叉树的过程：

1. 获取前序字符串的第一个字符A，它作为当前根节点，然后扫描中序字符串，找到A的位置，创建根节点存储结构。
2. 然后在中序字符串中确定左子树中序为CBD，再去前序字符串中截取相同长度的子串，确定左子树前序为BCD，有了左子树的前序和中序，就可以递归调用创建左子树，跟当前根节点关联起来。
3. 同样地，我们可以确定右子树的前序为EF，中序为EF，然后递归调用创建右子树，跟当前根节点关联起来。
4. 整个过程是递归的，直到前序和中序字符串只有一个字符时，直接创建叶子节点并跟父节点关联起来。

通过中序和后序构建二叉树跟上述过程类似，由后序确定当前根节点后，再通过中序确定左子树和右子树序列，然后递归创建左子树和右子树，并与当前根节点关联。

下面是实现代码：

JS版：

//二叉树节点结构
function BinTreeNode(data) {
  this.data = data;
  this.leftChild = null;
  this.rightChild = null;
}

//根据前序和中序创建二叉树
function createBinTreeByPreIn(preOrder, inOrder) {
  //如果只剩一个字符，则直接创建节点并返回
  if (preOrder.length === 1) {
    return new BinTreeNode(preOrder.charAt(0));
  }

  //从前序获取当前根节点字符
  var c = preOrder.charAt(0);

  //中序索引和前序节点个数
  var i = 0;
  var number = preOrder.length;

  //遍历中序序列，直到发现当前根节点
  while (i < number && inOrder.charAt(i) != c) i++;

  //求出左子树和右子树节点个数
  var leftNumber = i;
  var rightNumber = number - i - 1;

  //创建当前根节点
  var node = new BinTreeNode(c);

  //创建左子树
  if (leftNumber >= 1) {
    var leftPre = preOrder.substring(1, 1 + leftNumber);
    var leftIn = inOrder.substring(0, leftNumber);

    node.leftChild = createBinTreeByPreIn(leftPre, leftIn);
  }

  //创建右子树
  if (rightNumber >= 1) {
    var rightPre = preOrder.substring(leftNumber + 1);
    var rightIn = inOrder.substring(leftNumber + 1);

    node.rightChild = createBinTreeByPreIn(rightPre, rightIn);
  }

  //返回当前根节点
  return node;
}

//根据中序和后序创建二叉树
function createBinTreeByInPost(inOrder, postOrder) {
  //如果只剩一个字符，则直接创建节点并返回
  if (postOrder.length === 1) {
    return new BinTreeNode(postOrder.charAt(0));
  }

  //从后序获取当前根节点字符
  var c = postOrder.charAt(postOrder.length - 1);

  //中序索引和前序节点个数
  var i = 0;
  var number = postOrder.length;

  //遍历中序序列，直到发现当前根节点
  while (i < number && inOrder.charAt(i) != c) i++;

  //求出左子树和右子树节点个数
  var leftNumber = i;
  var rightNumber = number - i - 1;

  //创建当前根节点
  var node = new BinTreeNode(c);

  //创建左子树
  if (leftNumber >= 1) {
    var leftIn = inOrder.substring(0, leftNumber);
    var leftPost = postOrder.substring(0, leftNumber);

    node.leftChild = createBinTreeByInPost(leftIn, leftPost);
  }

  //创建右子树
  if (rightNumber >= 1) {
    var rightIn = inOrder.substring(leftNumber + 1);
    var rightPost = postOrder.substring(leftNumber, postOrder.length - 1);

    node.rightChild = createBinTreeByInPost(rightIn, rightPost);
  }

  //返回当前根节点
  return node;
}

//前序遍历
function preOrderTraverse(node, orderArray) {
  if (node) {
    orderArray.push(node.data);
    preOrderTraverse(node.leftChild, orderArray);
    preOrderTraverse(node.rightChild, orderArray);
  }
}

//后序遍历
function postOrderTraverse(node, orderArray) {
  if (node) {
    postOrderTraverse(node.leftChild, orderArray);
    postOrderTraverse(node.rightChild, orderArray);
    orderArray.push(node.data);
  }
}

//前序，中序，后序
var preOrder = 'ABCDEF';
var inOrder = 'CBDAEF';
var postOrder = 'CDBFEA';

//根据前序和中序创建二叉树
var binTree = createBinTreeByPreIn(preOrder, inOrder);

//用于存放节点遍历序列
var orderArray = [];

//后序遍历验证其正确性
postOrderTraverse(binTree, orderArray);
console.log('post order: ', orderArray.join(' '));

//清空遍历序列数组
orderArray.length = 0;

//根据中序和后序创建二叉树
binTree = createBinTreeByInPost(inOrder, postOrder);

//前序遍历验证其正确性
preOrderTraverse(binTree, orderArray);
console.log('pre order: ', orderArray.join(' '));

Java版：

//BinTreeNode.java

package algorithm;

//二叉树节点结构
public class BinTreeNode {
    private char data;
    private BinTreeNode leftChild;
    private BinTreeNode rightChild;

    public BinTreeNode(char data) {
        this.data = data;
    }

    public char getData() {
        return data;
    }

    public void setData(char data) {
        this.data = data;
    }

    public BinTreeNode getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(BinTreeNode leftChild) {
        this.leftChild = leftChild;
    }

    public BinTreeNode getRightChild() {
        return rightChild;
    }

    public void setRightChild(BinTreeNode rightChild) {
        this.rightChild = rightChild;
    }
}

//BinTreeCreator.java

package algorithm;

public class BinTreeCreator {

    //根据前序和中序创建二叉树
    public static BinTreeNode createBinTreeByPreIn(String pre, String in) {
        if (pre.length() == 1) {
            return new BinTreeNode(pre.charAt(0));
        }

        char c = pre.charAt(0);

        int i = 0;
        int number = pre.length();

        while (i < number && in.charAt(i) != c) i++;

        int leftNumber = i;
        int rightNumber = number - i - 1;

        BinTreeNode node = new BinTreeNode(c);

        if (leftNumber >= 1) {
            String leftPre = pre.substring(1, 1 + leftNumber);
            String leftIn = in.substring(0, leftNumber);

            node.setLeftChild(createBinTreeByPreIn(leftPre, leftIn));
        }

        if (rightNumber >= 1) {
            String rightPre = pre.substring(leftNumber + 1);
            String rightIn = in.substring(leftNumber + 1);

            node.setRightChild(createBinTreeByPreIn(rightPre, rightIn));
        }

        return node;
    }

    //根据中序和后序创建二叉树
    public static BinTreeNode createBinTreeByInPost(String in, String post) {
        if (post.length() == 1) {
            return new BinTreeNode(post.charAt(0));
        }

        char c = post.charAt(post.length() - 1);

        int i = 0;
        int number = post.length();

        while (i < number && in.charAt(i) != c) i++;

        int leftNumber = i;
        int rightNumber = number - i - 1;

        BinTreeNode node = new BinTreeNode(c);

        if (leftNumber >= 1) {
            String leftIn = in.substring(0, leftNumber);
            String leftPost = post.substring(0, leftNumber);

            node.setLeftChild(createBinTreeByInPost(leftIn, leftPost));
        }

        if (rightNumber >= 1) {
            String rightIn = in.substring(leftNumber + 1);
            String rightPost = post.substring(leftNumber, post.length() - 1);

            node.setRightChild(createBinTreeByInPost(rightIn, rightPost));
        }

        return node;
    }

    //前序遍历
    public static void preOrderTraverse(BinTreeNode node) {
        if (node != null) {
            System.out.print(node.getData());
            preOrderTraverse(node.getLeftChild());
            preOrderTraverse(node.getRightChild());
        }
    }

    //后序遍历
    public static void postOrderTraverse(BinTreeNode node) {
        if (node != null) {
            postOrderTraverse(node.getLeftChild());
            postOrderTraverse(node.getRightChild());
            System.out.print(node.getData());
        }
    }

    public static void main(String[] args) {
        String pre = "ABCDEF";
        String in = "CBDAEF";
        String post = "CDBFEA";

        BinTreeNode rootNode = BinTreeCreator.createBinTreeByPreIn(pre, in);
        System.out.print("post order: ");
        BinTreeCreator.postOrderTraverse(rootNode);

        rootNode = BinTreeCreator.createBinTreeByInPost(in, post);
        System.out.print(System.lineSeparator() + "pre order: ");
        BinTreeCreator.preOrderTraverse(rootNode);
    }
}

C语言版：

#include 
#include 

typedef struct node {
    char data;
    struct node *lchild, *rchild;
} BinTreeNode;

BinTreeNode * createBinTreeByPreIn(char *pre, char *in, int number);
BinTreeNode * createBinTreeByInPost(char *in, char *post, int number);
void preOrderTraverse(BinTreeNode *node);
void inOrderTraverse(BinTreeNode *node);
void postOrderTraverse(BinTreeNode *node);

int main(int argc, const char * argv[]) {

    char *pre = "ABCDEF";
    char *in = "CBDAEF";
    char *post = "CDBFEA";

    BinTreeNode *rootNode = createBinTreeByPreIn(pre, in, 6);

    printf("post order: ");
    postOrderTraverse(rootNode);

    rootNode = createBinTreeByInPost(in, post, 6);

    printf("\npre order: ");
    preOrderTraverse(rootNode);

    return 0;
}

//根据前序和中序创建二叉树
BinTreeNode * createBinTreeByPreIn(char *pre, char *in, int number) {
    if (number == 0) return NULL;

    char c = pre[0];

    int i = 0;

    while (i < number && in[i] != c) i++;

    int leftNumber = i;
    int rightNumber = number - i - 1;

    BinTreeNode *node = (BinTreeNode *) malloc(sizeof(BinTreeNode));
    node->data = c;

    node->lchild = createBinTreeByPreIn(&pre[1], &in[0], leftNumber);

    node->rchild = createBinTreeByPreIn(&pre[leftNumber + 1], &in[leftNumber + 1], rightNumber);

    return node;
}

//根据中序和后序创建二叉树
BinTreeNode * createBinTreeByInPost(char *in, char *post, int number) {
    if (number == 0) return NULL;

    char c = post[number - 1];

    int i = 0;

    while (i < number && in[i] != c) i++;

    int leftNumber = i;
    int rightNumber = number - i - 1;

    BinTreeNode *node = (BinTreeNode *) malloc(sizeof(BinTreeNode));
    node->data = c;

    node->lchild = createBinTreeByInPost(&in[0], &post[0], leftNumber);

    node->rchild = createBinTreeByInPost(&in[leftNumber + 1], &post[leftNumber], rightNumber);

    return node;
}

//前序遍历
void preOrderTraverse(BinTreeNode *node) {
    if (node != NULL) {
        printf("%c", node->data);

        preOrderTraverse(node->lchild);

        preOrderTraverse(node->rchild);
    }
}

//后序遍历
void postOrderTraverse(BinTreeNode *node) {
    if (node != NULL) {
        postOrderTraverse(node->lchild);

        postOrderTraverse(node->rchild);

        printf("%c", node->data);
    }
}