「CERC2017」Embedding Enumeration-DP
Description
给定一个 n n n 个点的树。你需要将它放到一个 2 × n 2 \times n 2×n 的网格里，每个格子至多放一个点，在树上相邻的点在网格中也必须相邻，并且 1 1 1 号点必须放在左上角。
求方案数对 1 0 9 + 7 10^9+7 109+7 取模的结果。
n ≤ 1 0 5 n \leq 10^5 n≤105
Solution
设 f u f_u fu表示把 u u u放在左上角的方案数。
- u u u是叶子。显然 f u = 1 f_u=1 fu=1。
- u u u有一个儿子 v v v。
- 这个儿子放在下面。
- 这个儿子是叶子。显然直接 + 1 +1 +1。
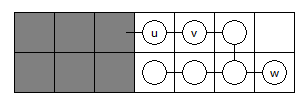
- 这个儿子有一个儿子 w w w。显然 f w → f u f_w\to f_u fw→fu。
- 这个儿子放在右边。设 k k k为其子树中第一个度数不为 2 2 2的点。
- 显然可以 f v → f u f_v \to f_u fv→fu
- k k k为叶子。当且仅当 d i s ( u , k ) m o d 2 = 0 dis(u,k)mod\ 2 = 0 dis(u,k)mod 2=0且 d i s ( u , k ) > 2 dis(u,k)>2 dis(u,k)>2时， f u f_u fu加一。
- k k k度数为 3 3 3。
- 共有 4 4 4种情况。
- f w → f u f_w\to f_u fw→fu
- f w → f u f_w\to f_u fw→fu
- f u f_u fu加一（两条链一样长）
- f y → f u f_y\to f_u fy→fu（ y y y所在链更长）
- f w → f u f_w\to f_u fw→fu
- 共有 4 4 4种情况。
- 这个儿子放在下面。
- 当 u u u的度数为 3 3 3时，转移与上述转移的最后后两种类似。不做赘述。
以上诸如 k , w , y k,w,y k,w,y节点的查找。可以通过预处理每个点到它子树中第一个度数不是 2 2 2的点（包括这个点）及到这个点的距离 O ( 1 ) O(1) O(1)计算。
复杂度 O ( n ) O(n) O(n)。
#include