DTMF信号的分离——关于一篇博客文章的复现（二）

上一回，我们阐述了一下我们的目标以及整理了一下我们的解决方案。接下来就需要上代码了。不过在此之前，有几点我需要说明一下：
1、由于本人没有找到DTMF信号的音频，且手头也没有老式的电话机，因此自己用MATLAB写了一个产生DTMF信号的音频，这个音频是没有杂波的，所以从时域图上看非常的邪门，这个不重要，只要频率分量正常就好；
2、本着方便的原则，我只写了1、2、3、4、5、6、7、8、9这九个数字的DTMF信号，包括后期的模式识别和特征提取，也只针对这九个数字，有需要的朋友可以稍微改一下代码，即可实现全部字符的识别；
3、代码自己写的，水平可能比较差，各位轻喷…….

---

我们先回顾一下我们的思路：
分帧——绘制全频率语谱图——频率量化——绘制区间频率语谱图——特征提取——特征匹配——分类——得到号码。
在此之前，我们首先需要有一个DTMF信号，这个程序很容易：

function voice = dtmf(x)
%函数用来生成DTMF音频信号
%输入参数：
%               x:为一段数字序列，要求长度为11
%输出参数：
%               voice:x对应的DTMF音频信号，要求Fs=8K

f_row=[1209 1336 1477 1633];
f_col=[697 770 852 941];
fs=8000;%采样频率
% t=0.5%每个音持续的时间
% ts=1/fs;%采样间隔
% t=[0:ts:t]
x1=add_sin(f_row(1),f_col(1),fs);%1对应的信号
x2=add_sin(f_row(2),f_col(1),fs);%2对应的信号
x3=add_sin(f_row(3),f_col(1),fs);%3对应的信号
x4=add_sin(f_row(1),f_col(2),fs);%4对应的信号
x5=add_sin(f_row(2),f_col(2),fs);%5对应的信号
x6=add_sin(f_row(3),f_col(2),fs);%6对应的信号
x7=add_sin(f_row(1),f_col(3),fs);%7对应的信号
x8=add_sin(f_row(2),f_col(3),fs);%8对应的信号
x9=add_sin(f_row(3),f_col(3),fs);%8对应的信号
zero=zeros(1,4800);
xn=cell(1,9);yn=cell(1,11);
xn={x1,x2,x3,x4,x5,x6,x7,x8,x9};
for k=1:11
    yn{k}=xn{x(k)};
end
for k=1:11
    yn{k}=[yn{k} zero];
end
yn=[yn{1} yn{2} yn{3} yn{4} yn{5} yn{6} yn{7} yn{8} yn{9} yn{10} yn{11}];
audiowrite([num2str(x),'.wav'],yn,fs);
end

只要将你的电话号码保存为一个x向量，调用这个函数即可生成一个音频文件，这个音频文件将是一个标准的、没有干扰的DTMF信号，如下图：

第一步是分帧，分帧程序我之前已经写好，这下直接调用就行了。我选择的帧时长为0.1s，帧步进值为0.08s。关于帧长和步进的问题，后面还会提到，暂时先取这两个值。程序如下：

[xn,fs]=audioread('data1.wav');%data1为DTMF信号音频文件
fram_time=0.1;%帧时长
fram_step_time=0.08;%帧步进
win='hamming';
[row col]=size(xn);
if row>col xn=xn';
else
end

ts=1/fs;

l=length(xn);%序列的总长度
xn_time=l*ts;%序列的总时长
fram_length=ceil(fram_time/ts);%每一帧的长度
fram_step_length=ceil(fram_step_time/ts);%帧移的长度
if win=='hanning' win=hanning(fram_length);
elseif win=='hamming' win=hamming(fram_length);
end
%帧数的计算公式为：序列点数-帧长度+帧移）/帧移
numOfframs=(l-fram_length+fram_step_length)/fram_step_length;%计算得到帧数
%考虑到序列总长度和分帧结果不匹配，补0以满足分帧要求
numOfframs=ceil(numOfframs);
%反算为了满足分帧序列应该增加的长度
l_added=(numOfframs*fram_step_length-fram_step_length+fram_length);%得到序列应该有的长度
l=l_added-l;
xn=[xn,zeros(1,l)];%补0
xn_time=ceil(l*ts);
xn_frams=zeros(fram_length,numOfframs);%建立存放结果的矩阵

%开始分帧
for k=1:numOfframs
    dn=(k-1)*fram_step_length+(1:fram_length);
    xn_frams(:,k)=xn(dn).*win';
end

经过分帧过程，原本的信号已经被分成了800帧，每帧97个数据的片段（可从WorkSpace看到）。
那么在分帧结束后，就要绘制全频率语谱图了。为什么我要加一个“全频率”呢？因为截止到现在，我还没有对频率进行量化，我们又知道虽然我的信号在产生的时候，全部是基于单频信号叠加而成，但由于计算机处理的信号只能是有限长的信号，因此这时候的信号频率，不再和一个“无限长的正弦单频信号”相同。尽管它的确就是来源于“无限长的正弦单频信号”。加上DFT或FFT的算法原因，此时的DTMF信号，将会含有很多的频率分量，在没有量化的条件下，它们是丰富的。我们可以对DTMF信号直接做FFT来观察一下这个现象。

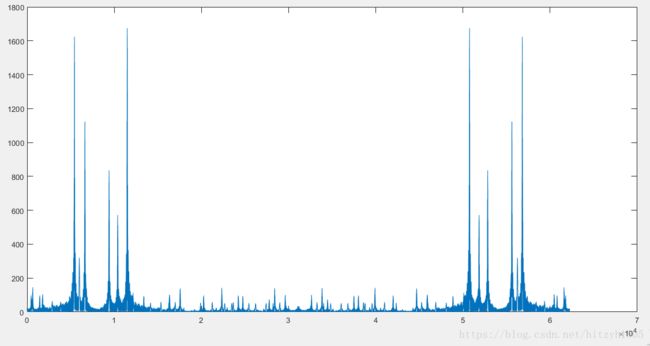
可以看到，DTMF信号不仅仅是由单频信号组成的，它的频率分量是丰富的，尽管能量最高的几个频率是显然的，但这仍不足以让我们把它们挨个分出来，因此量化是必须的。但这是后话，眼下，我们的工作是“基于这些丰富的频率，绘制信号的语谱图”。
语谱图反映的是信号频率在时间上的分布特性。
代码如下：

[fram_length,numOfframs]=size(xn_frams)
%首先建立一个频率轴，因为每一帧的长度都是相同的，所以所有帧可以共用同一个频率轴
f=fs*[0:fram_length-1].*(1/fram_length);
f_length=length(f);
f_length=ceil(f_length/2);%向下取整
f=f(1:f_length);%仅取在物理上有实际意义的频率

%再建立一个时间轴，时间轴是针对整个完整信号而言的，并不是针对
%每一帧，因此时间轴上的每一个刻度应该是具体每一帧的开始时间
time=[0:fram_step_time:l_added*ts-fram_step_time];

%建立一个空矩阵，用来存放每一帧fft的结果
fftframs=zeros(fram_length,numOfframs);
fftframs(:,1:numOfframs)=abs(fft(xn_frams(:,1:numOfframs)));%将每一帧FFT的结果存在矩阵fftframs中
fftframs_end=zeros(ceil(fram_length/2),numOfframs);
fftframs_end=fftframs(1:ceil(fram_length/2),:);
imagesc(time,f,fftframs_end); %画出语谱图
xlabel('时间/s');ylabel('频率/Hz');

我们得到的语谱图是这样的：

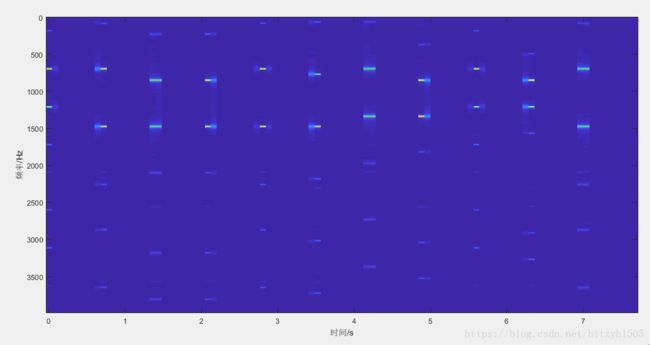
这幅图怎么看呢？
如果大家能耐心的读完这段绘制语谱图的代码。我们至少可以明确这么几点：
1、语谱图是针对帧而言的，换言之，它在描述帧；
2、语谱图上有两个要素，一个是时间，一个是频率；
代码中用到了一个函数，叫做imagesc(time,f,fftframs_end)。这个函数的主要作用是：以“time”和“f”为横轴和纵轴，矩阵”fftframs_end”中的每一个元素的值作为一个像素点绘制一副像素图。值越大，颜色越深。
因此，time和f正好就是fftframs_end的行数和列数。
在这个图中，我们可以发现，每隔一段时间，都会出现一块小黄斑，同一时间还会出现两块，这是横轴告诉我们的。纵轴方向上，每个小黄斑对应一个频率，这是纵轴告诉我们的。细心的朋友还会发现，小黄斑出现的时间，基本和DTMF信号波形图中有声音的时间吻合。看到这里，语谱图的意义大家应该都懂了：“某个时间段的信号，含有某频率的分量”。
如果大家仔细观察图片，甚至可以直接读出这段电话号码来，但这很麻烦，而且频率不够精准，所以，接下来需要做的就是频率量化了。
频率量化的必要性之前已经说过，此处不再赘述，关键在于如何选定分界点。考虑到我需要识别的九个频率分别是：
697Hz ， 770Hz ， 852Hz ， 1209Hz ， 1336Hz ， 1477Hz
我分别选取了：
0 720Hz 800Hz 1100Hz 1270Hz 1400Hz 3900Hz为分界点，这样可以把整个频率量化为6个部分，分别对应我们的6个基本频率。具体代码：

f_new=[0 720 800 1100 1270 1400 3900]
for i=2:7
    pos1=find(f_new(i-1)==f);
    pos2=find(f==f_new(i));
    fftframs_new(i-1,:)=sum(fftframs_end(pos1:pos2,:));
end
f_new=[1 2 3 4 5 6];figure(2);
imagesc(time,f_new,fftframs_new); %画出语谱图
xlabel('时间/s');ylabel('频率/Hz');

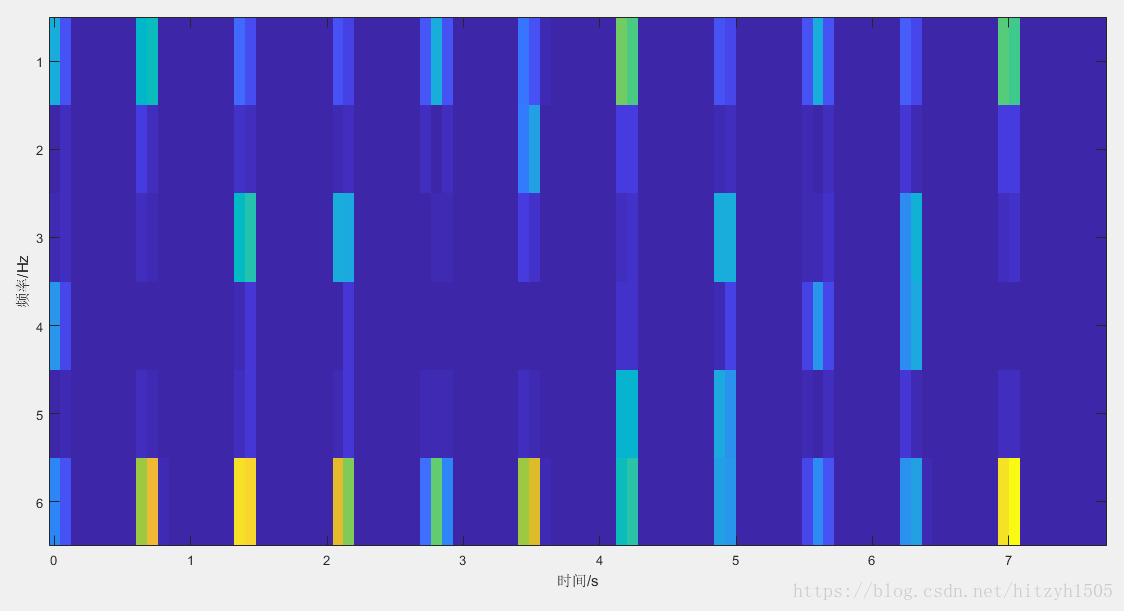
大家可以从图中看到，频率轴已经被量化成了6个部分，而之前非常难以观察的小黄斑也变长了，更加容易观察了。

---

既然频率可以量化，并且量化后使得我们需要的要素在图中变得更加明显，那么时间也一定可以量化，但是时间是否需要量化呢？答案是肯定的。并且时间量化之后，图中的要素也更加显然。这一点，我们放在下篇文章中细细道来。