算法-二叉树-前序、中序、后序遍历图解+python3实现
0.简介
本文主要内容有:
- 介绍二叉树概念
- 使用图解,简单直观地阐述了二叉树前序、中序、后序遍历的方法
- 使用python3 编程实现二叉树,并进行了前序、中序、后序遍历。
1.二叉树概念(来源于百度百科)
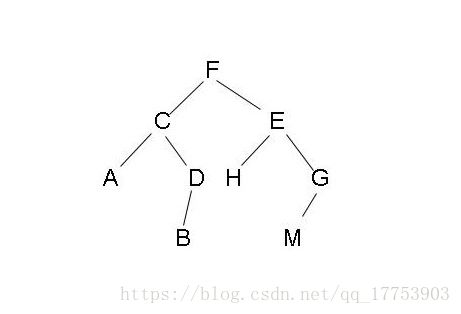
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
2.二叉树的前序、中序、后序三种遍历方式
前序遍历:根节点 --> 左子树 -->右子树
中序遍历:左子树 -->根节点 -->右子树
后序遍历: 左子树 -->右子树 -->根节点
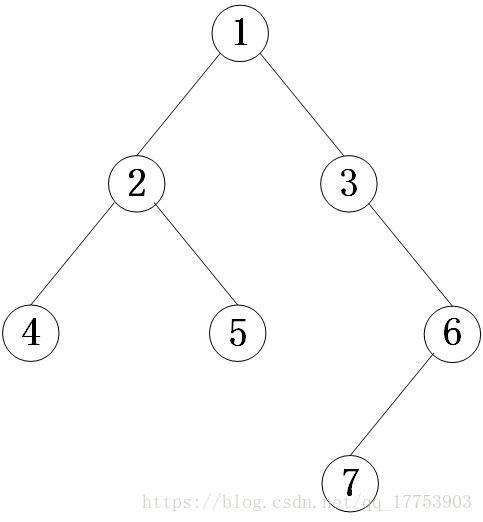
上图只是简单介绍了原理,下面来看一个更为复杂的二叉树:
先给出结果:
前序遍历:[1,2,4,5,3,6,7]
中序遍历:[4,2,5,1,3,7,6]
后序遍历:[4,5,2,7,6,3,1]
下面以中序遍历为例,详细讲解遍历过程:
中序遍历:左子树 -->根节点 -->右子树
step1:
先找到根节点1;
发现1有左子树,是2,因此跳转到左子树2的遍历过程;
发现2有左子树,是4,因此跳转到左子树4的遍历过程;
发现4没有左子树,不需要继续跳转,也不输出;
4是子树根节点,输出:4
发现4没有右子树,不需要继续跳转,也不输出;
该层子树遍历完成,跳回到上一层子树中。
step2:
2的左子树遍历完成;
2是子树根节点,输出:2
发现2有右子树,是5,因此跳转到右子树5的遍历过程;
step3:
发现5没有左子树,不需要继续跳转,也不输出;
5是子树根节点,输出:5
发现5没有右子树,不需要继续跳转,也不输出;
该子树遍历完成,跳回到上一层子树中。
step4:
该层子树遍历完成,跳回到上一层子树中。
step5:
1的左子树遍历完成;
1是子树根节点,输出:1
发现1有右子树,是3,因此跳转到右子树3的遍历过程;
step6:
发现3没有左子树,不需要继续跳转,也不输出;
3是子树根节点,输出:3
发现3有右子树,是6,因此跳转到右子树6的遍历过程
step7:
发现6有左子树,是7,因此跳转到左子树4的遍历过程;
发现7没有左子树,不需要继续跳转,也不输出;
7是子树根节点,输出:7
发现7没有右子树,不需要继续跳转,也不输出;
该层子树遍历完成,跳回到上一层子树中。
step8:
6的左子树遍历完成;
6是子树根节点,输出:6
发现6没有右子树,不需要继续跳转,也不输出;
step9:
该层子树遍历完成,跳回到上一层子树中。
step10:
该层子树遍历完成,所有书遍历完成。
3.程序示例
通过上面的分析步骤可以看出,遍历可以基于递归进行。
输入:列表,按照前序遍历的顺序,存放二叉树节点名称。其中,为空的子树,用'NIL'表示。
node_list = [1,2,4,'NIL','NIL',5,'NIL','NIL',3,'NIL',6,7,'NIL','NIL','NIL']输出:前序、中序、后序遍历结果
class Node:
def __init__(self,root="NIL",left=None,right=None):
self.root = root
self.left = left
self.right = right
self.out_list_temp = []
class Tree(Node):
def build(self,node_list):
root = node_list.pop(0)
if root == "NIL":
tree = None
else:
tree = Tree(root)
tree.left = self.build(node_list)
tree.right = self.build(node_list)
return tree
def preorder_traversal(self,tree):
if (tree.root != None):
self.out_list_temp.append(tree.root)
if tree.left != None:
self.preorder_traversal(tree.left)
if tree.right != None:
self.preorder_traversal(tree.right)
return self.out_list_temp
def preorder_traversal_print(self,tree):
print(self.preorder_traversal(tree))
self.out_list_temp = []
def inorder_traversal(self,tree):
if tree.left != None:
self.inorder_traversal(tree.left)
if (tree.root != None):
self.out_list_temp.append(tree.root)
if tree.right != None:
self.inorder_traversal(tree.right)
return self.out_list_temp
def inorder_traversal_print(self,tree):
print(self.inorder_traversal(tree))
self.out_list_temp = []
def postorder_traversal(self,tree):
if tree.left != None:
self.postorder_traversal(tree.left)
if tree.right != None:
self.postorder_traversal(tree.right)
if (tree.root != None):
self.out_list_temp.append(tree.root)
return self.out_list_temp
def postorder_traversal_print(self,tree):
print(self.postorder_traversal(tree))
self.out_list_temp = []
if __name__ == '__main__':
node_list = [1,2,4,'NIL','NIL',5,'NIL','NIL',3,'NIL',6,7,'NIL','NIL','NIL']
tree = Tree()
my_tree = tree.build(node_list)
tree.preorder_traversal_print(my_tree)
tree.inorder_traversal_print(my_tree)
tree.postorder_traversal_print(my_tree)
#result:
#[1, 2, 4, 5, 3, 6, 7]
#[4, 2, 5, 1, 3, 7, 6]
#[4, 5, 2, 7, 6, 3, 1]