Codeforces 1230C Anadi and Domino 枚举

C. Anadi and Domino

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

Anadi has a set of dominoes. Every domino has two parts, and each part contains some dots. For every a and b such that 1 ≤ a ≤ b ≤ 6, 1 ≤ a ≤ b ≤ 6, there is exactly one domino with a dots on one half and b dots on the other half. The set contains exactly 21 dominoes. Here is an exact illustration of his set:

Also, Anadi has an undirected graph without self-loops and multiple edges. He wants to choose some dominoes and place them on the edges of this graph. He can use at most one domino of each type. Each edge can fit at most one domino. It's not necessary to place a domino on each edge of the graph.

When placing a domino on an edge, he also chooses its direction. In other words, one half of any placed domino must be directed toward one of the endpoints of the edge and the other half must be directed toward the other endpoint. There's a catch: if there are multiple halves of dominoes directed toward the same vertex, each of these halves must contain the same number of dots.

How many dominoes at most can Anadi place on the edges of his graph?

Input

The first line contains two integers n and m (1 ≤ n ≤ 7, 1 ≤ n ≤ 7, 0 ≤ m ≤ n⋅(n−1)/2) — the number of vertices and the number of edges in the graph.

The next m lines contain two integers each. Integers in the i-th line are ai and bi (1 ≤ a, b ≤ n, 1 ≤ a, b ≤ n, a ≠ b, a ≠ b) and denote that there is an edge which connects vertices ai and bi.

The graph might be disconnected. It's however guaranteed that the graph doesn't contain any self-loops, and that there is at most one edge between any pair of vertices.

Output

Output one integer which denotes the maximum number of dominoes which Anadi can place on the edges of the graph.

Examples

input

4 4
1 2
2 3
3 4
4 1

output

4

input

7 0

output

0

input

3 1
1 3

output

1

input

7 21
1 2
1 3
1 4
1 5
1 6
1 7
2 3
2 4
2 5
2 6
2 7
3 4
3 5
3 6
3 7
4 5
4 6
4 7
5 6
5 7
6 7

output

16

Note

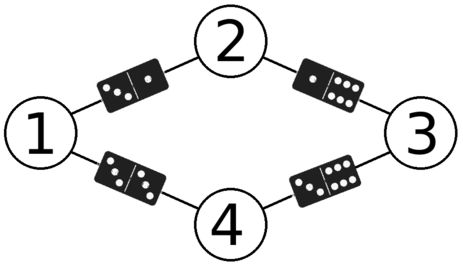
Here is an illustration of Anadi's graph from the first sample test:

 

And here is one of the ways to place a domino on each of its edges:

Note that each vertex is faced by the halves of dominoes with the same number of dots. For instance, all halves directed toward vertex 11 have three dots.

 

题意

有如图所示的 21 个多米诺骨牌，给定一个无向图（无自环，无重边），一条边上可以放置一个多米诺骨牌。要求是如果两条边连接同一个顶点，那就必须使这两条边上的多米诺骨牌指向这个顶点的值相等，可以有不放的情况，问给定的图中最多可以放多少个多米诺骨牌。

分析

假设每个顶点都有一个值，这个值就是构造完成后这个顶点所连接的边上放的多米诺骨牌指向它的值。

当 n < 7 时，不管有多少个顶点多少条边，都可以放满，因此结果将等于 m 。

当 n == 7 时，因为多米诺骨牌中的数字最大只到 6 ，因此我们假设在有七个顶点时有一个数字是被重复使用了的。数字并不一定是节点的编号这点一定要注意。然后我们枚举这个被重复使用的点（因为它在 1-6  之间），如何枚举？每次枚举数字相同的顶点对，即下面代码中的 i 和 j，假设他们代表的数字是相同的，然后通过 cnt 计数有多少条边需要被放弃，因为每张多米诺骨牌只能使用一次。

代码

#include 
#include 
#include 
using namespace std;
#define INF 0x3f3f3f3f
typedef long long LL;

int d[10][10];

int main()
{
    int n, m, a, b;
    cin >> n >> m;
    for(int i = 0; i < m; i++){
        cin >> a >> b;
        d[a][b] = 1;
        d[b][a] = 1;
    }
    if(n < 7){ 
        cout << m << endl;
    }
    else {
        int ans = INF;
        for(int i = 1; i <= 7; i++){  //假设i和j是数字相同的顶点
            for(int j = i + 1; j <= 7; j++){
                int cnt = 0;
                for(int k = 1; k <= 7; k++){
                    if(d[i][k] && d[j][k]) cnt++;  // cnt记录如果这样有多少条边要被放弃
                }
                ans = min(ans, cnt);
            }
        }
        cout << m - ans << endl;
    }
    return 0;
}