二叉树后序遍历的四种方法

在二叉树三种顺序的遍历中，后序遍历相对较麻烦一些，其实对于递归方法来说，三种方法大同小异，思路与实现都很简单。后序遍历的迭代法与Morris方法比较麻烦。这里介绍后序遍历的四种方法，其实还是递归、迭代和Morris方法，只不过在迭代中有几种实现方式。

1、递归法

直接上代码：

//recursion
class Solution1 {
public:
    vector postorderTraversal(TreeNode* root) {
        vector ret;
        postHelper(ret,root);
        return ret;
    }
private:
    void postHelper(vector& ret,TreeNode* root)
    {
        if(root==NULL)return;
        postHelper(ret,root->left);
        postHelper(ret,root->right);
        ret.push_back(root->val);
    }
};

2、迭代法

迭代法使用一个栈来保存当前不需要访问的节点。不过，不同于中序遍历与前序遍历，在后序遍历中每一个节点需要一个标志位，来标识当前节点的左右子树是否被访问。因为在后序遍历中，只有一个节点的左右子树被访问后它才能被访问。因此，压入栈中的数据类型需要是一个pair，其中用1来表示当前节点的左右子树正被访问，当再次访问到此节点时可以访问此节点；用0表示当前节点的左右子树未被访问，再次访问到此节点时需要首先访问此节点的左右子树。代码如下：

//iteration
class Solution1 {
public:
    vector postorderTraversal(TreeNode* root) {
        vector ret;
        if(root==NULL)return ret;
        stack> st;
        st.push(make_pair(root,0));
        while(!st.empty())
        {
            TreeNode *curr=st.top().first;
            if(st.top().second==1)
            {
                ret.push_back(curr->val);
                st.pop();
            }
            else
            {
                st.top().second=1;
                if(curr->right)st.push(make_pair(curr->right,0));
                if(curr->left)st.push(make_pair(curr->left,0));
            }
        }
        return ret;
    }
};

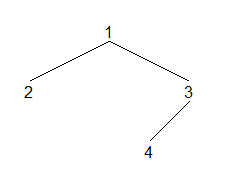
例如，对于如下的二叉树，运行过程如下：

（1）节点1

栈中内容（左侧是TreeNode*，这里用节点内容表示，右侧是标志位）：

1	0

结果：[]

（2）节点1

标志位是0，不能访问当前节点，添加右儿子和左儿子，同时将标志位置为1：

栈中内容：

2	0
3	0
1	1

结果：[]

（3）节点2

标识位是0，不能访问，添加右儿子和左儿子。由于均为空，不添加，将标志位置为1；

栈中内容：

2	1
3	0
1	1

结果：[]

（4）节点2

标志位是1，可以访问，访问后弹出。

栈中内容：

3	0
1	1

结果;[2]

（5）节点3

标志位是0，不能访问，添加子节点。并将标志位置为1；

栈中内容：

4	0
3	1
1	1

结果：[2]

（5）节点4

标志位是0，不能访问，添加子节点并将标志位置为1；

栈中内容：

4	1
3	1
1	1

结果：[2]

（6）节点4

标志位是1，可以访问，访问后弹出；

栈中内容：

3	1
1	1

结果：[2,1]

（7）节点3

标志位是1，可以访问，访问后弹出；

栈中内容：

1	1

结果：[2,4,3]

（8）节点1

标志位是1，可以访问，访问后弹出；

栈中内容：

结果：[2,4,3,1]

至此，栈为空，循环结束。可以看到，这种方式每个节点需要访问两次。

3、迭代法：按照根、右、左的顺序访问然后取反

这种方法就是按照根、右、左的顺序访问，然后将结果取反即可。后序遍历的顺序是左、右、根。这种方法就可以在前序遍历的基础上修改即可。代码如下：

class Solution3 {
public:
    vector postorderTraversal(TreeNode* root) {
        vector ret;
        if(root==NULL)return ret;
        stack st;
        st.push(root);
        while(!st.empty())
        {
            TreeNode *curr=st.top();
            st.pop();
            if(curr->left)st.push(curr->left);
            if(curr->right)st.push(curr->right);
            ret.push_back(curr->val);
        }
        reverse(ret.begin(),ret.end());
        return ret;
    }
};

在按照根、右、左的顺序遍历时，每个节点访问一遍，最后将结果取反时，每个节点也访问一遍，因此节点的总访问次数和方法2相同。

4、Morris方法

后序遍历的Morris方法思路比较难。但整体上还是一样的，对原来的二叉树的修改也是一样的，不同的是访问的顺序。而在后序遍历中，访问时比较麻烦。下面是整个算法的工作过程;

首先建立一个临时节点dump，令其左儿子是root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。
步骤：
当前节点设置为临时节点dump。
（1）如果当前节点的左儿子为空，则将其右儿子作为当前节点；
（2）如果当前节点的左儿子非空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点；
   a) 如果前驱节点的右孩子为空，将它的右儿子设置为当前节点。当前节点更新为当前节点的左儿子；
   b) 如果前驱节点的右儿子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左儿子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右儿子；
（3）重复以上（1）（2）直到当前节点为空。

代码如下：

//morris
class Solution4 {
public:
    vector postorderTraversal(TreeNode* root) {
        vector ret;
        TreeNode *dump=new TreeNode(0);
        dump->left=root;
        TreeNode *curr=dump;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    reverseAddNodes(curr->left,pre,ret);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
private:
    void reverseAddNodes(TreeNode *begin,TreeNode *end,vector& ret)
    {
        reverseNodes(begin,end);
        TreeNode *curr=end;
        while(true)
        {
            ret.push_back(curr->val);
            if(curr==begin)break;
            curr=curr->right;
        }
        reverseNodes(end,begin);
    }
    void reverseNodes(TreeNode *begin,TreeNode *end)
    {
        TreeNode *pre=begin;
        TreeNode *curr=pre->right;
        TreeNode *post;
        while(pre!=end)
        {
            post=curr->right;
            curr->right=pre;
            pre=curr;
            curr=post;
        }
    }
};