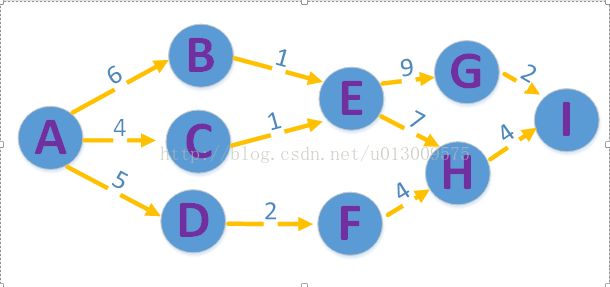
拓扑排序和关键路径

 

拓扑排序:

       每次选择前驱节点为0的节点,然后删除以其为顶点的边,重复上述操作,直到删除所有节点为止或者所有节点都有前驱.若还有剩余节点,那么图存在环.

关键路径(图中最长的路径):

活动:图中的弧.

事件:图中的顶点.

由于活动时间长短可能不同,导致事件发生的时间可以不同,从v1到vi的最长路径长度是节点i的最早发生时间,不推迟整个工程完成的情况下,事件vi的最迟开始时间.

1.根据拓扑序,更新所有节点的最早发生时间,使其最大.

2.令终点的最迟开始时间等于最早发生时间.

3.根据逆拓扑序,更新所有节点的最迟开始时间,使其最小.

4.如果一个节点的最迟开始时间等于最早发生时间,那么该事件为关键事件,如果一条弧两端的节点都是关键事件,那么该弧为关键活动.这样就可以查找到所有关键活动了.

 

(1)为什么要根据拓扑序来扩展节点?

       因为当拓扑序扩展到某一个节点时候,该节点已经没有前驱了.所以可以到达该节点的路径都已经计算过了,即该节点所记录的路径值为v0到达vi的最大值.

(2)为什么要根据逆拓扑序来计算最迟开始时间?

       如果一个图可以进行拓扑排序,那么把该图中所有路径首尾倒置,即箭头方向调转,该图也一定可以进行拓扑排序,且和倒转前的图的拓扑排序恰好相反.这样,我们可以把逆拓扑序看作路径倒转后的拓扑序.这样根据上面的拓扑序扩展原理,此处我们使用逆拓扑序可以令扩展出来的节点的最迟开始时间最小

 

#include
#include
#include
#include
 
usingnamespace std;
#defineVexNum 9
#defineVEXMAX 100000
typedefchar VextexType;
typedefint  EdgeType;
 
 
structEdgeNode;
structEdgeNode {
    VextexType HeadName;
    VextexType TailName;
    EdgeType  weight;
    EdgeNode  *VexOut;
    EdgeNode  *VexIn;
  
};
 
structvexTopological {
    char name;
    int preVexNum;
    int early;
    int last;
    bool isUsed;
}vextopo[VexNum];
 
structvexWeight{
    char name;
    int pathWeight;
    char path[VexNum+1];
};
 
typedefstruct
{
    VextexType name;
    EdgeNode  *VexOutlink;
    EdgeNode  *VexInlink;
}VexNode;
 
VexNodeadjList[VexNum];
 
 
 
 
voidcreatGraph()
{
 
    VextexType vextemp;
    EdgeType  edgetemp;
    //char a[]={'A','B','C','D','E'};
    char a[]={'A', 'B', 'C', 'D', 'E', 'F','G', 'H', 'I'};
    int b[] = {
        0, 6, 4, 5, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 1, 0, 0, 0, 0,
        0, 0, 0, 0, 1, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 2, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 9, 7, 0,
        0, 0, 0, 0, 0, 0, 0, 4, 0,
        0, 0, 0, 0, 0 ,0 ,0, 0, 2,
        0, 0, 0, 0 ,0 ,0, 0, 0, 4,
        0, 0, 0, 0, 0, 0, 0, 0, 0};
    //input n vextex
    for ( int i=0; i>vextemp;
        //vextemp = a[i];
        adjList[i].name       = vextemp;
        adjList[i].VexOutlink = NULL;
        adjList[i].VexInlink  = NULL;
    }
    for ( int i=0; i>edgetemp;
        //edgetemp = b[i];
        if ( edgetemp==0 ){
            continue;
        }
 
        EdgeNode *pEdge = new EdgeNode;
        pEdge->HeadName =adjList[i/VexNum].name;
        pEdge->TailName =adjList[i%VexNum].name;
        pEdge->weight   = edgetemp;
 
        pEdge->VexOut   = adjList[i/VexNum].VexOutlink;
        if ( pEdge->VexOut ){
            while ( pEdge->VexOut->VexOut){
                pEdge->VexOut=pEdge->VexOut->VexOut;
            }
            pEdge->VexOut->VexOut =pEdge;
            pEdge->VexOut=NULL;
        } else {
            adjList[i/VexNum].VexOutlink =pEdge;
            pEdge->VexOut = NULL;
        }
    }
    for ( int i=0 ;iTailName !=adjList[i].name ){
                    p = p->VexOut;
                    continue;
                }
                *pInLink = p;
                pInLink = &p->VexIn;
                p = p->VexOut;
            }
        }
        *pInLink = NULL;
    }
}
 
voiddestroyGrape()
{
    for ( int i=0; iVexOut;
            delete q;
        }
    }
 
 
}
 
voidprintGrape()
{
    for ( int i=0; i";
        EdgeNode *p = adjList[i].VexOutlink;
        while ( p ){
           cout<<"("<HeadName<<","<TailName<<","<weight<<")";
            p = p->VexOut;
        }
        cout<";
        while ( p ){
           cout<<"("<HeadName<<","<TailName<<","<weight<<")";
            p = p->VexIn;
        }
        cout< s;
    deque sPrint;
    for ( int i=0; iVexIn;
            vextopoNum++;
        }
        vextopo[i].preVexNum = vextopoNum;
    }
 
    //按拓扑顺序压入栈中.
    for ( int i=0; iTailName-'A';
            if ( vextopo[nextNum].early <(vextopo[i].early + pNext->weight) ){
                vextopo[nextNum].early =vextopo[i].early + pNext->weight;
            }
            vextopo[nextNum].preVexNum--;
            pNext = pNext->VexOut;
        }   
    }
 
    ptopo = s.top();
    s.pop();
    ptopo->last = ptopo->early;
    s.push(ptopo);
    while ( !s.empty() ){
        int vexPos;
        int preVexPos;
 
        ptopo = s.top();
        s.pop();
       
        vexPos = ptopo->name-'A';
        pPre = adjList[vexPos].VexInlink;
        while ( pPre ){
            preVexPos = pPre->HeadName-'A';
            if ( vextopo[preVexPos].last >ptopo->last - pPre->weight ){
                vextopo[preVexPos].last  = ptopo->last - pPre->weight;
            }
            pPre = pPre->VexIn;
        }
    }
    while ( !sPrint.empty() ){
        vexTopological * p = sPrint.front();
        sPrint.pop_front();
        if ( p->early != p->last ){
            continue;
        }
        int vexPos = p->name - 'A';
        EdgeNode * pedge =adjList[vexPos].VexOutlink;
        while ( pedge ){
            if (vextopo[pedge->TailName-'A'].last == vextopo[pedge->TailName-'A'].early){
               cout<<"("<HeadName<<","<TailName<<","<weight<<")";
            }
            pedge = pedge->VexOut;
        }
 
    }
}
 
int main()
{
    creatGraph();
    printGrape();
    topologicRank();
    destroyGrape();
}

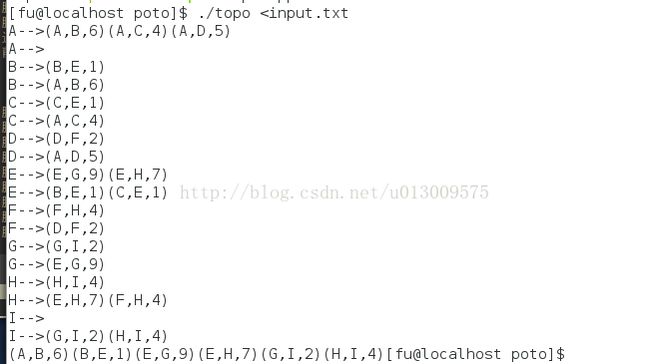
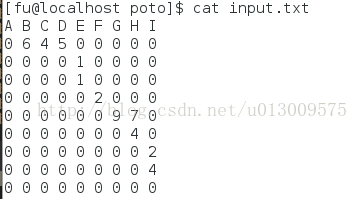
测试数据: