HDU-6535 计算几何 辛普森积分

Problem Description
Chika has just learned about solid geometry! She is very interested in the volume of three-dimensional geometric shapes, so she decides to test you.
Before that, she is going to tell you definitions of the following two three-dimensional geometric shapes.

Oblique circular cone: A cone whose surface is generated by lines joining a fixed point called the apex to the points of a circle, the fixed point lying on a line that is not perpendicular to the circle at its center. (The circular cone is a special kind of oblique circular cone.)

Pyramid: A polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided base has n+1 vertices, n+1 faces, and 2n edges.

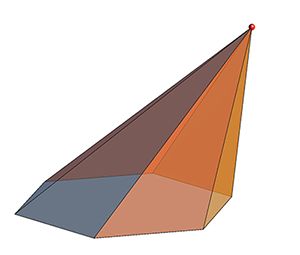
Chika gives you an oblique circular cone and a pyramid placed in the space rectangular coordinate system. Their bottoms are on the plane z=0. The z-coordinates of their apexes are bigger than 0. Some parts of them may overlap with each other. You need to help Chika to calculate the volume of the union of the two three-dimensional geometric shapes.

Input
The input file contains several lines.
The first line contains three integers x, y, z (z>0), which are the coordinates of the apex of the oblique circular cone.
The second row contains three integers x, y and r (r>0). x and y are the x-coordinate and the y-coordinate of the center of the oblique circular cone’s bottom circle. r is radius of the oblique circular cones’s bottom circle.
The third line contains three integers x, y, z (z>0), which are the coordinates of the apex of the pyramid.
The fourth line contains a positive integer n (n≤1000), which is the number of vertices of the pyramid’s bottom polygon.
Then n lines follow. Each line contains two integers x, y, which are the x-coordinate and y-coordinate of the n vertices of the pyramid’s bottom polygon. Vertex coordinates are given in counterclockwise order. These points do not coincide.
It is guaranteed that the absolute values of all input integers are not greater than 1000.

Output
The output file should contain only one line, including one real number, representing the volume of the union of the oblique circular cone and the pyramid. The relative error or absolute error between your answer and the standard answer should be less than 10−6.

Sample Input
0 0 2
2 0 2
0 0 2
3
2 0
4 -2
4 2

Sample Output
8.9498519738

将立体物体用平面z=h切割，切出圆和多边形
三角剖分求圆与多边形的面积交，S并=S圆+S多边形-S交
面积微元ds按Z轴积分即可
注意两物体，积到顶点及以上部分时就特判面积=0

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxp=1024;
const double inf=1e200;
const double eps=1e-8;
const double pi =acos(-1.0);
int sgn(double x){
	if(fabs(x)<eps)return 0;
	return x>0?1:-1;
}
struct Point{
	double x,y;
	Point(double x=0,double y=0):x(x),y(y){}
	bool operator ==(const Point& b){return !sgn(x-b.x)&&!sgn(y-b.y);}
	bool operator  <(const Point& b)const{return !sgn(x-b.x)?y<b.y:x<b.x;}
	double operator^(const Point& b){return x*b.y-y*b.x;}//叉积
	double operator*(const Point& b){return x*b.x+y*b.y;}//点积
	Point operator +(const Point &b){return Point(x+b.x,y+b.y);}
	Point operator -(const Point& b){return Point(x-b.x,y-b.y);}
	Point operator *(const double &k){return Point(x*k,y*k);}
	Point operator /(const double &k){return Point(x/k,y/k);}
	double len(){return hypot(x,y);}
	double len2(){return x*x+y*y;}
	double rad(Point a,Point b){Point p=*this;return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p)));}//pa和pb夹角
	double angle(){return atan2(y,x);}//倾斜角
	double angle(Point B){//夹角
		Point A=(*this);
		return acos(A*B/A.len()/B.len());
	}
	double distance(Point b){return hypot(x-b.x,y-b.y);}
	Point trunc(double r){//化为长度为r的向量
		double l=len();
		if(!sgn(l))return *this;
		r/=l;return Point(x*r,y*r);
	}
	Point rotleft(){return Point(-y,x);}//逆时针旋转90 度
	Point rotright(){return Point(y,-x);}//顺时针旋转90 度
	Point rotate(double rad){//rad为弧度 逆时针旋转
		Point A=(*this);
		double c=cos(rad),s=sin(rad);
		return Point(A.x*c-A.y*s,A.x*s+A.y*c);
	}
	Point rotate(Point p,double angle){//绕p逆时针旋转后点
		Point v=((*this)-p).rotate(angle);
		return Point(p.x+v.x,p.y+v.y);
	}
	void input(){scanf("%lf%lf",&x,&y);}
	void show(){printf("(%.2lf %.2lf)\n",x,y);}
	void zero(){
		if(!sgn(x))x=0.0;
		if(!sgn(y))y=0.0;
	}
};
double cross(Point A,Point B,Point C){return (B-A)^(C-A);}//AB X AC
double dot(Point A,Point B,Point C){return (B-A)*(C-A);}//AB*AC
struct Line{
	Point s,e;
	Line(){};
	Line(Point s,Point e):s(s),e(e){};
	double len(){return s.distance(e);}
	double dispointtoline(Point p){return fabs((p-s)^(e-s))/len();}//点到直线的距离
	Point lineprog(Point p){return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2()));}//返回点p 在直线上的投影
};
struct circle{
	Point p;//圆心
	double r;//半径
	circle(){}
	circle(Point p,double r):p(p),r(r){}
	int relation(Point b){//点和圆的关系//0 圆外//1 圆上//2 圆内
		double dst=b.distance(p);
		if(sgn(dst-r)<0)return 2;
		else if(!sgn(dst-r))return 1;
		return 0;
	}
	int relationline(Line v){//直线与圆关系
		double dst=v.dispointtoline(p);
		if(sgn(dst-r)<0)return 2;
		else if(!sgn(dst-r))return 1;
		return 0;
	}
	int pointcrossline(Line v,Point &p1,Point &p2){//求直线和圆的交点，返回交点个数
		if(!(*this).relationline(v))return 0;
		Point a=v.lineprog(p);
		double d=v.dispointtoline(p);
		d=sqrt(r*r-d*d);
		if(!sgn(d)){p1=p2=a;return 1;}
		p1=a+(v.e-v.s).trunc(d);
		p2=a-(v.e-v.s).trunc(d);
		return 2;
	}
	double areatriangle(Point a,Point b){//求圆和三角形pab 的相交面积//测试：POJ3675 HDU3982 HDU2892
		if(!sgn((p-a)^(p-b)))return 0.0;
		Point q[5],p1,p2;
		int len=0;
		q[len++]=a;
		Line l(a,b);
		if(pointcrossline(l,q[1],q[2])==2){
			if(sgn((a-q[1])*(b-q[1]))<0)q[len++]=q[1];
			if(sgn((a-q[2])*(b-q[2]))<0)q[len++]=q[2];
		}q[len++]=b;
		if(len==4&&sgn((q[0]-q[1])*(q[2]-q[1]))>0)swap(q[1],q[2]);
		double res=0;
		for(int i=0;i<len-1;++i){
			if(!relation(q[i])||!relation(q[i+1]))res+=r*r*p.rad(q[i],q[i+1])/2.0;
			else res+=fabs((q[i]-p)^(q[i+1]-p))/2.0;
		}return res;
	}
	double area(){return pi*r*r;}
	void input(){p.input(),scanf("%lf",&r);}
};
struct polygon{
	int n;
	Point p[maxp];
	void input(int _n){n=_n;for(int i=0;i<n;++i)p[i].input();}
	void add(Point q){p[n++]=q;}
	double areacircle(circle c){//多边形和圆交的面积
		double ans=0;
		for(int i=0;i<n;++i){
			int j=(i+1)%n;
			if(sgn((p[j]-c.p)^(p[i]-c.p))>=0)ans+=c.areatriangle(p[i],p[j]);
			else ans-=c.areatriangle(p[i],p[j]);
		}return fabs(ans);
	}
	double getarea(){//得到面积
		double sum=0;
		for(int i=0;i<n;++i)sum+=(p[i]^p[(i+1)%n]);
		return fabs(sum)/2;
	}
};
circle O,newo;
polygon A,newa;
Point tp,tmp;
double x,y,z,x1,y1,z1;
double F(double h){//目标积分函数
	double rad=1-(z-h)/z;
	if(sgn(rad-1.0)<0)newo=circle(O.p+tp.trunc(tp.len()*rad),O.r*(1-rad));
	else newo=circle(Point(0,0),0);
	newa.n=0;
	rad=1-(z1-h)/z1;
	if(sgn(rad-1.0)<0)for(int i=0;i<A.n;++i){
		tmp=Point(x1-A.p[i].x,y1-A.p[i].y);
		newa.add(A.p[i]+tmp.trunc(tmp.len()*rad));
	}
	return newa.getarea()+newo.area()-newa.areacircle(newo);
}
double simpson(double a,double b){
	double c=a+(b-a)/2;
	return (F(a)+4*F(c)+F(b))*(b-a)/6;
}
double asr(double a,double b,double eps,double A){
	double c=a+(b-a)/2;
	double L=simpson(a,c),R=simpson(c,b);
	if(fabs(L+R-A)<=15*eps) return L+R+(L+R-A)/15.0;
	return asr(a,c,eps/2,L)+asr(c,b,eps/2,R);
}
double asr(double a,double b,double eps){//调用这个 a左 b右
	return asr(a,b,eps,simpson(a,b));
}
int n;
int main(){
	while(~scanf("%lf%lf%lf",&x,&y,&z)){
		O.input();
		scanf("%lf%lf%lf",&x1,&y1,&z1);
		scanf("%d",&n);
		A.input(n);
		tp=Point(x-O.p.x,y-O.p.y);
		printf("%.10lf\n",asr(0,max(z,z1),1e-7));
	}
	return 0;
}