三次样条插值实现函数拟合
数值分析实验——三次样条插值
GoatWu
一、程序摘要
此程序使用 python3.7 语言编写。引入了外部库函数 numpy 作为数学工具解方程,matplotlib 作为画图工具。由于需要多步运行,对不同的参数进行绘图,因此使用了 jupyter-notebook 作为编写工具。
由于用到的函数较多,为了安全起见,此程序将内部函数封装在了 Functions.py 模块中,将接口函数封装在了 spline.py 模块中。在 spline.py 中,我们引用了 Functions.py 的内部函数;在主程序中,我们只需要引入 spline 模块即可:import spline as sp。
程序有两个接口。第一个接口函数的功能是,对于给定的函数,在给定的范围中均匀选点,然后进行三次样条插值进行拟合;第二个接口函数的功能是,对于给定的点集与边界条件,将这些点利用三次样条插值进行拟合。下面我们将逐一呈现。
二、程序功能
1. 给定函数的拟合
接口:sp.give_func(func = F.runge, beg = -5, end = 5, segments = 10)
参数意义:
func:需要拟合的函数。默认值为 Functions 中的龙格函数beg:拟合范围的左端点end:拟合范围的右端点segments:拟合的区间个数,也即点的个数减 1 1 1
使用示例:
sp.give_func():
在 [ − 5 , 5 ] [-5,5] [−5,5] 的范围内用 10 10 10 段拟合龙格函数
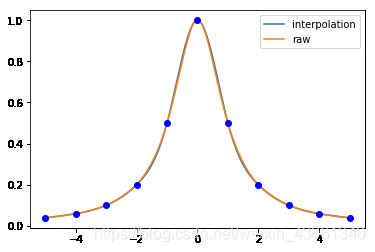
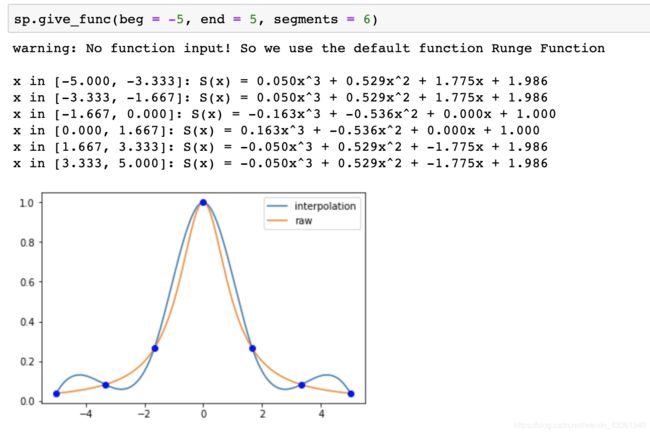
sp.give_func(beg = -5, end = 5, segments = 6):
在 [ − 5 , 5 ] [-5,5] [−5,5] 的范围内用 6 6 6 段拟合龙格函数。
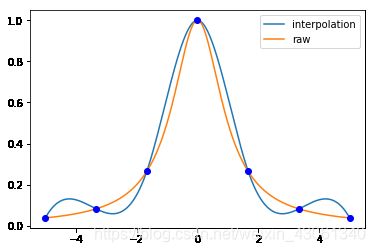
-
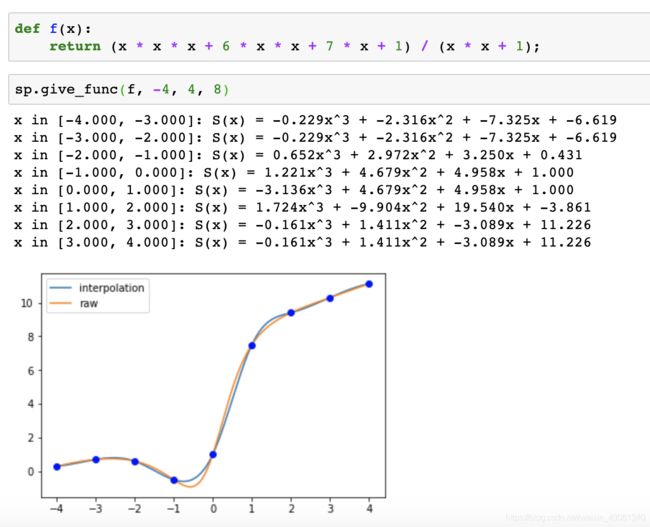
def f(x): return (x * x * x + 6 * x * x + 7 * x + 1) / (x * x + 1); sp.give_func(f, -4, 4, 8)
对自定义的函数 f ( x ) = x 3 + 6 x 2 + 7 x + 1 x 2 + 1 f(x)=\frac{x^3+6x^2+7x+1}{x^2+1} f(x)=x2+1x3+6x2+7x+1 ,分 8 8 8 段 在区间 [ − 4 , 4 ] [-4,4] [−4,4] 来拟合函数。
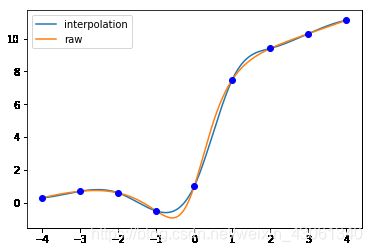
2. 给定点集的拟合
接口:sp.give_nodes(x, y, opt = 0, lval = 0, rval = 0)
参数意义:
x:给定点集的 x x x 坐标数组y:给定点集的 y y y 坐标数组opt:插值的边界条件opt = 0:默认边界条件,左右两端点处的三阶导与前一端点处三阶导相等opt = 1:给定左右两端点的一阶导,分别为lval和rval。opt = 2:给定左右两端点的二阶导,分别为lval和rval。
使用示例:
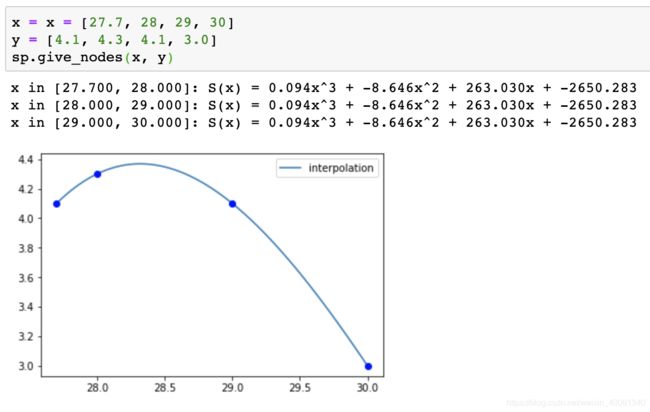
x = x = [27.7, 28, 29, 30]
y = [4.1, 4.3, 4.1, 3.0]
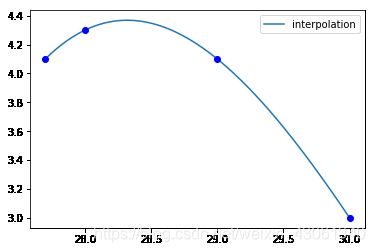
sp.give_nodes(x, y):
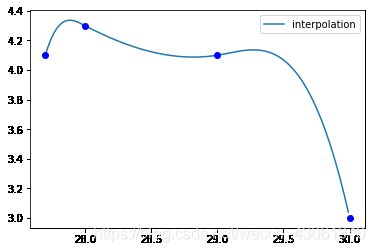
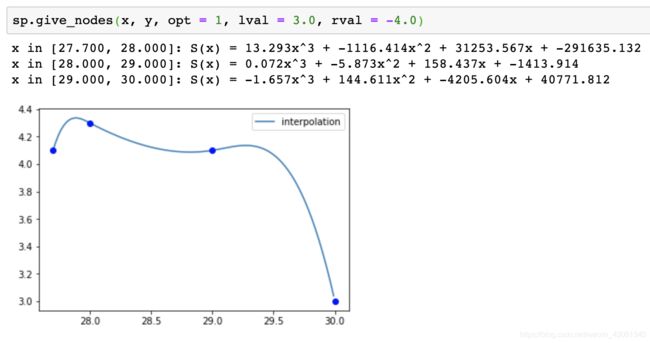
sp.give_nodes(x, y, opt = 1, lval = 3.0, rval = -4.0):
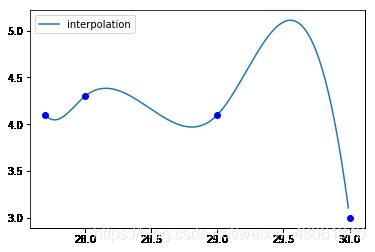
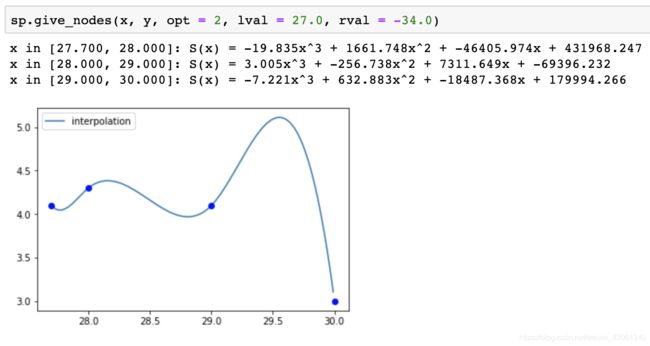
sp.give_nodes(x, y, opt = 2, lval = 27.0, rval = -34.0):
3. 给出各分段的三次函数表达式
三、程序的鲁棒性
1. 无给定函数的提示
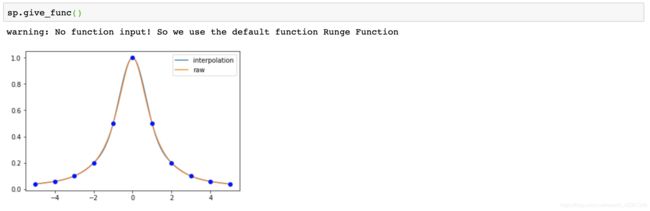
对于给定函数的拟合,在无输入函数的情况下,默认使用龙格函数,并弹出提示:
2. 错误的 opt 参数
对于给定点集的拟合,如果 opt 参数不为有意义的值,返回错误:
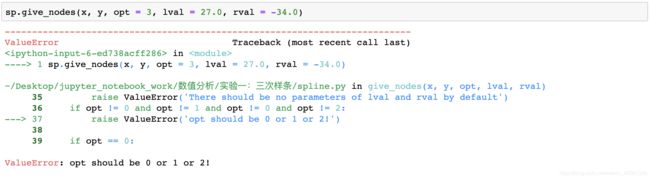
3. 额外的 lval 或 rval 值
对于给定点集的拟合,如果 opt = 0 下,仍给出lval 或 rval 值,返回错误:
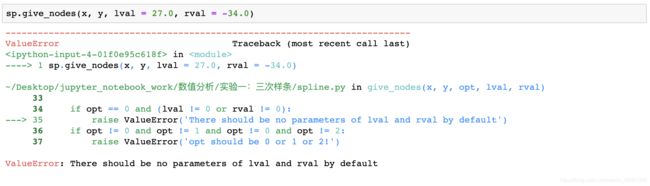
4. 给定点集的 x 和 y 长度不等
对于给定点集的拟合,如果 x 数组和 y 数组长度不等,返回错误:
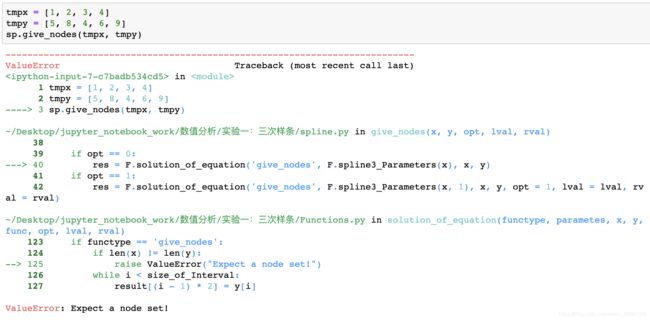
四、部分程序运行结果
1. 给定函数的拟合
1.1. 龙格函数
1.2. 给定其他函数
2. 给定点集的拟合
2.1. 默认情况
2.2. 给定一阶导的边界条件
2.3. 给定二阶导的边界条件
五、程序源代码
1. Functions.py
import math
import numpy as np
import matplotlib.pyplot as plt
def runge(y):
y = np.float32(y)
return 1/(1 + y * y)
def spline3_Parameters(x_vec, opt = 0):
# 建立三对角矩阵的 4n 个方程的左边部分
# parameter为二维数组,用来存放参数,size_of_Interval为区间的个数
x_new = np.array(x_vec)
parameter = []
size_of_Interval = len(x_new) - 1;
i = 1
# 相邻两区间公共节点处函数值相等的方程,共2n-2个
while i < len(x_new) - 1:
data = np.zeros(size_of_Interval * 4)
data[(i - 1) * 4] = x_new[i] * x_new[i] * x_new[i]
data[(i - 1) * 4 + 1] = x_new[i] * x_new[i]
data[(i - 1) * 4 + 2] = x_new[i]
data[(i - 1) * 4 + 3] = 1
parameter.append(data)
data = np.zeros(size_of_Interval * 4)
data[i * 4] = x_new[i] * x_new[i] * x_new[i]
data[i * 4 + 1] = x_new[i] * x_new[i]
data[i * 4 + 2] = x_new[i]
data[i * 4 + 3] = 1
parameter.append(data)
i += 1
# 左右端点处的函数值。为两个方程, 加上前面的2n-2个方程,一共2n个方程
data = np.zeros(size_of_Interval * 4)
data[0] = x_new[0] * x_new[0] * x_new[0]
data[1] = x_new[0] * x_new[0]
data[2] = x_new[0]
data[3] = 1
parameter.append(data)
data = np.zeros(size_of_Interval * 4)
data[(size_of_Interval - 1) * 4] = x_new[-1] * x_new[-1] * x_new[-1]
data[(size_of_Interval - 1) * 4 + 1] = x_new[-1] * x_new[-1]
data[(size_of_Interval - 1) * 4 + 2] = x_new[-1]
data[(size_of_Interval - 1) * 4 + 3] = 1
parameter.append(data)
# 端点函数一阶导数值相等为n-1个方程。加上前面的方程为3n-1个方程。
i = 1
while i < size_of_Interval:
data = np.zeros(size_of_Interval * 4)
data[(i - 1) * 4] = 3 * x_new[i] * x_new[i]
data[(i - 1) * 4 + 1] = 2 * x_new[i]
data[(i - 1) * 4 + 2] = 1
data[i * 4] = -3 * x_new[i] * x_new[i]
data[i * 4 + 1] = -2 * x_new[i]
data[i * 4 + 2] = -1
parameter.append(data)
i += 1
# 端点函数二阶导数值相等为n-1个方程。加上前面的方程为4n-2个方程。
i = 1
while i < len(x_new) - 1:
data = np.zeros(size_of_Interval * 4)
data[(i - 1) * 4] = 6 * x_new[i]
data[(i - 1) * 4 + 1] = 2
data[i * 4] = -6 * x_new[i]
data[i * 4 + 1] = -2
parameter.append(data)
i += 1
# 两个附加条件
# 默认情况:opt = 0,not-a-knot边界条件:左边两端点三阶导相等,右边两端点三阶导也相等
if opt == 0:
data = np.zeros(size_of_Interval * 4)
data[0] = 6
data[4] = -6
parameter.append(data)
data = np.zeros(size_of_Interval * 4)
data[-4] = 6
data[-8] = -6
parameter.append(data)
# opt = 1,给定左右两端点的一阶导值
if opt == 1:
data = np.zeros(size_of_Interval * 4)
data[0] = 3 * x_new[0] * x_new[0]
data[1] = 2 * x_new[0]
data[2] = 1
parameter.append(data)
data = np.zeros(size_of_Interval * 4)
data[-4] = 3 * x_new[-1] * x_new[-1]
data[-3] = 2 * x_new[-1]
data[-2] = 1
parameter.append(data)
# opt = 2,给定左右两端点的二阶导值
if opt == 2:
data = np.zeros(size_of_Interval * 4)
data[0] = 6 * x_new[0]
data[1] = 2
parameter.append(data)
data = np.zeros(size_of_Interval * 4)
data[-4] = 6 * x_new[-1]
data[-3] = 2
parameter.append(data)
return parameter
def solution_of_equation(functype, parametes, x, y = 0, func = runge, opt = 0, lval = 0, rval = 0):
# 建立三对角线性方程组并求解,得到各段三次函数的系数并返回
# functype 表示需要拟合的是给定函数 / 给定点集
size_of_Interval = len(x) - 1;
result = np.zeros(size_of_Interval * 4)
i = 1
if functype != 'give_func' and functype != 'give_nodes':
raise ValueError("functype should be 'give_func' or 'give_nodes' ")
if functype == 'give_func':
while i < size_of_Interval:
result[(i - 1) * 2] = func(x[i])
result[(i - 1) * 2 + 1] = func(x[i])
i += 1
result[(size_of_Interval - 1) * 2] = func(x[0])
result[(size_of_Interval - 1) * 2 + 1] = func(x[-1])
if functype == 'give_nodes':
if len(x) != len(y):
raise ValueError("Expect a node set!")
while i < size_of_Interval:
result[(i - 1) * 2] = y[i]
result[(i - 1) * 2 + 1] = y[i]
i += 1
result[(size_of_Interval - 1) * 2] = y[0]
result[(size_of_Interval - 1) * 2 + 1] = y[-1]
# 默认情况:opt = 0,not-a-knot边界条件:左边两端点三阶导相等,右边两端点三阶导也相等
if opt == 0:
result[-2] = result[-1] = 0;
# opt = 1 或 opt = 2,给定左右两端点的一阶导值 / 二阶导值
if opt == 1 or opt == 2:
result[-2] = lval
result[-1] = rval
a = np.array(parametes)
b = np.array(result)
return np.linalg.solve(a, b)
def calculate(paremeters, x):
# 计算x在拟合得到的函数中的点值
res = []
for dx in x:
res.append(paremeters[0] * dx * dx * dx + paremeters[1] * dx * dx + paremeters[2] * dx + paremeters[3])
return res
def draw_pic(functype, x, y, func = runge, xnd = 0, ynd = 0):
fig = plt.figure()
plt.plot(x, y, label='interpolation')
if functype == 'give_func':
plt.plot(x, func(x), label='raw')
l = len(xnd)
for i in range(0, l):
plt.plot(xnd[i], ynd[i], 'bo')
plt.legend()
plt.show()
plt.close(fig)
2. spline.py
import Functions as F
import numpy as np
def give_func(func = F.runge, beg = -5, end = 5, segments = 10):
if func == F.runge:
print("warning: No function input! So we use the default function Runge Function\n")
interval = 1.0 * (end - beg) / segments
x_init4 = np.arange(beg, end + 0.0001, interval)
res = F.solution_of_equation('give_func', F.spline3_Parameters(x_init4), x_init4, y = 0, func = func)
x_axis4 = []
y_axis4 = []
xnd = []
ynd = []
for i in range(segments):
temp = np.arange(beg + i * interval, beg + (i + 1) * interval, 0.01)
xid = beg + i * interval
xnd = np.append(xnd, xid)
ynd = np.append(ynd, F.calculate([res[4 * i], res[1 + 4 * i], res[2 + 4 * i], res[3 + 4 * i]], np.array([xid])))
x_axis4 = np.append(x_axis4, temp)
y_axis4 = np.append(y_axis4, F.calculate([res[4 * i], res[1 + 4 * i], res[2 + 4 * i], res[3 + 4 * i]], temp))
i = segments - 1
xid = beg + (i + 1) * interval
xnd = np.append(xnd, xid)
ynd = np.append(ynd, F.calculate([res[4 * i], res[1 + 4 * i], res[2 + 4 * i], res[3 + 4 * i]], np.array([xid])))
for i in range(len(xnd) - 1):
print(f"x in [{xnd[i]:.3f}, {xnd[i+1]:.3f}]: S(x) = {res[4*i]:.3f}x^3 + {res[1+4*i]:.3f}x^2 + {res[2+4*i]:.3f}x + {res[3+4*i]:.3f}")
F.draw_pic("give_func", x_axis4, y_axis4, func, xnd, ynd)
def give_nodes(x, y, opt = 0, lval = 0, rval = 0):
if opt == 0 and (lval != 0 or rval != 0):
raise ValueError('There should be no parameters of lval and rval by default')
if opt != 0 and opt != 1 and opt != 0 and opt != 2:
raise ValueError('opt should be 0 or 1 or 2!')
if opt == 0:
res = F.solution_of_equation('give_nodes', F.spline3_Parameters(x), x, y)
if opt == 1:
res = F.solution_of_equation('give_nodes', F.spline3_Parameters(x, 1), x, y, opt = 1, lval = lval, rval = rval)
if opt == 2:
res = F.solution_of_equation('give_nodes', F.spline3_Parameters(x, 2), x, y, opt = 2, lval = lval, rval = rval)
for i in range(len(x) - 1):
print(f"x in [{x[i]:.3f}, {x[i+1]:.3f}]: S(x) = {res[4*i]:.3f}x^3 + {res[1+4*i]:.3f}x^2 + {res[2+4*i]:.3f}x + {res[3+4*i]:.3f}")
x_axis4 = []
y_axis4 = []
for i in range(len(x) - 1):
temp = np.arange(x[i], x[i + 1], 0.01)
x_axis4 = np.append(x_axis4, temp)
y_axis4 = np.append(y_axis4, F.calculate([res[4 * i], res[1 + 4 * i], res[2 + 4 * i], res[3 + 4 * i]], temp))
F.draw_pic("give_nodes", x_axis4, y_axis4, func = None, xnd = x, ynd = y)
3. main.py
以下代码最好在 jupyter-notebook 中分条运行!如果是在 pycharm 等 ide 下或者是 sublime 等文本编辑器,需要将其余代码注释掉再分别运行。
import spline as sp
# 接口函数一:give_func(func = function, beg = -5, end = 5, segments = 10)
# 函数意义:对给定的函数,在 [beg, end] 范围内进行拟合,共 segments 段(即 segments+1 个点)
# 参数意义:func表示需要拟合的函数,默认为龙格函数;
# beg、end表示插值的范围,segments表示插值的数量。默认值写在上面。
sp.give_func()
sp.give_func(beg = -5, end = 5, segments = 6)
def f(x):
return (x * x * x + 6 * x * x + 7 * x + 1) / (x * x + 1);
sp.give_func(f, -4, 4, 8)
# 接口函数二:give_nodes(x, y, opt = 0, lval = 0, rval = 0)
# 函数意义:对于给定的点集进行插值
# 参数意义:x,y 表示点集的坐标;
# opt表示边界条件的处理:
# opt = 0 表示默认边界条件,not-a-knot边界条件:左边两端点三阶导相等,右边两端点三阶导也相等
# opt = 1 或 opt = 2,表示给定左右两端点的一阶导值 / 二阶导值
x = x = [27.7, 28, 29, 30]
y = [4.1, 4.3, 4.1, 3.0]
sp.give_nodes(x, y)
sp.give_nodes(x, y, opt = 1, lval = 3.0, rval = -4.0)
sp.give_nodes(x, y, opt = 2, lval = 27.0, rval = -34.0)
六、总结
此程序仅仅调用了 python 的外部库函数 numpy 用于解三对角矩阵方程,matplotlib 用于绘图,具有较好的独立性;兼容常用的两种边界条件,并且仿照 Matlab 自带的三次样条插值,设置了默认的 “两边三阶导与前一节点三阶导相等” 的边界条件;做了良好的封装,内部函数封装在 Functions 中不可被调用,并且支持多种的插值方式,对于错误的输入也能给予响应,具有较好的通用性。此程序的复杂度瓶颈在于解三对角矩阵方程,由于 numpy 强大的性能,也拥有良好的运行效率,在感受上运行几乎无延迟。