密码学基础概念(二)
1.1密码学的基本概念
1、什么是密码学
密码学是保密学的一部分。保密学是研究密码系统或通信安全的科学,它实际上包含两个分支——密码学和密码分析学。密码学是对信息进行编码实现隐蔽信息的一门科学;而密码分析学是研究分析如何破解密码的学问。两者相互独立,又相互促进,正如病毒技术和反病毒技术一样。
采用密码技术可以隐藏和保护需要保密的信息,使未经授权者不能提取信息。需要隐藏的消息称为“明文”;明文被变换成的另一种隐蔽的形式就是“密文”。这种变换称为“加密”;加密的逆过程,即从密文恢复出对应的明文的过程称为“解密”。对明文进行加密时采用的一组规则(函数)称为“加密算法”。对密文解密时使用的算法称为“解密算法”。一般地,加密算法和解密算法都是在一组密钥控制之下进行的,加密时使用的密钥称之为“加密密钥”,解密时使用的密钥称之为“解密密钥”。
2、密码系统的分类
密码系统通常从3个独立的方面进行分类:
(1)按将明文转换成密文的操作类型可以分为:置换密码和易位密码。
所有加密算法都是建立在两个通用的原则上的:置换和易位。置换是指将明文的每一个元素(比特、字母、比特或字母的组合)映射成其他的元素。如最古老的一种置换密码是由Julius Caesar发明的凯撒密码,这种密码算法是将明文中的每一个字母都用该字母后的第n个字母代替,其中n就是密钥。显然这种密码体制中的密钥空间只有26个密钥,只要知道用的是凯撒密码,破译者只需尝试25次,就可以知道正确的密码了。
易位是对明文的元素进行重新布置,但并不隐藏它们,即明文中的所有字母都可以从密文中找到,只是位置不一样。列易位密码是一种常用的易位密码。
大多数实用的密码算法都是用了多级置换及易位。无论如何进行置换和易位,总之,没有信息丢失是最基本的要求,也就是说,所有的操作都应该是可逆的。
(2)按照明文的处理方式可分为:分组密码和序列密码。
分组密码又称为“块密码(block cipher)”,它每次处理一块输入元素,每个输入块生成一个输出块。序列密码又称为“流密码(stream cipher),它对输入元素进行连续处理,每次生成一个输出块。
(3)按密码体制中密钥使用的个数可以分为:对称密码体制和非对称密码体制。
如果加密操作和解密操作采用的是相同的密钥,或者从一个密钥易于得出另一个密钥,这样的系统就叫做“对称密码系统”,也称为“密钥密码体制”。如果加密使用的密钥和解密使用的密钥不相同,且从一个密钥难以推出另一个密钥,这样的密码系统称为“非对称密码系统”,也称为“公钥密码体制”。
3、未来的密码——量子密码
随着物理学和信息科学的发展与交融,研究人员发现:以微观粒子作为信息的载体,利用量子技术,可以解决许多传统信息论无法处理或是难以处理的问题。“量子密码”的概念就是在这种背景下提出的。
当前,量子密码研究的核心内容,就是如何利用量子技术在量子信道上安全可靠地分配密钥。在信息保密中,密钥的地位是举足轻重的。但是,如何安全可靠、迅速高效地分配密钥,一直是密码学领域的一大难题。与传统密码学不同,量子密码学利用物理学原理保护信息。
通常把以量子为信息载体,经由量子信道传送,在合法用户之间建立共享的密钥的方法,称为量子密钥分配(QKD),其安全性由“海森堡测不准原理”及“单量子不可复制定理”保证。“海森堡测不准原理”是量子力学的基本原理,它表明,在同一时刻以相同的精度测定量子的位置与动量是不可能的,只能精确测定两者之一。“单量子不可复制定理”是“海森堡测不准原理”的推论,它表明,在不知道量子状态的情况下复制单个量子是不可能的,因为要复制单个量子就只能先作测量,而测量必然改变量子的状态,所以说不可能。量子的上述特性可以用来解决密钥的分配问题,从而突破传统信息论的束缚,设计出无条件安全的密码。
1.2 密码体制及其安全性
1.密码体制与密码函数
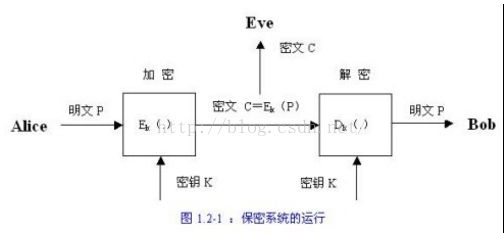
1949年,Claude Shannon在《Bell System Technical Journal》上发表了题为《Communication Theory of Security System》的论文。这篇论文对密码学的研究产生了巨大的影响。在这篇著作中对保密系统的运行做了如下的描述:
通信双方Alice和Bob通过一个安全信道进行相互协商,确定了一个共享的密钥K 。
Alice欲通过一个不安全的信道向Bob发送明文信息P;Alice使用钥控加密算法Ek( · )将明文P变换为密文C,C=Ek(P);Alice通过不安全的信道将密文C发送给Bob。
Bob使用钥控解密算法Dk( · )将密文C变换成明文P,P=Dk(C)。
截听者Eve在不安全的信道上截获了密文C,他试图进行攻击(攻击的方式有:被动攻击,破解密文C,从而得到明文P或密钥K;主动攻击,即毁坏或篡改密文以达到破坏明文的目的)。
具体过程见下图(图1.2-1):
以上所描述的五位一体 ( P,C,K,Ek( · ),Dk( · ) )就是一个密码体制,其中Ek( · ),Dk( · )都是密码函数。一般地说,信息安全工程中的消息加密方案和认证方案统称为密码体制,所使用的函数统称为密码函数。
对于以上的例子,有如下4点需要说明:
(1)Alice和Bob之间的安全信道通常是低速的,不能直接用于消息传递,否则就没有必要在不安全的信道上发送加密信息了。在安全信道上只能进行密钥协商,而且不能太频繁,这就是说安全信道的低速率使我们不能太频繁的更换密钥。
(2)作为消息加密方案中使用的密码函数,即加密算法Ek( · )和解密算法Dk( · )的设计必须满足各种各样的置乱功能。比如,当两个密钥K1和K2不相同时,Ek1( · )和Ek2( · )应该“差别很大”。又比如,当两个明文P1和P2 “差别很小”时,它们对应的密文C1和C2应该“差别很大”;反之亦然。这些置乱功能统称为“伪随机性”。(注:作为认证方案中使用的某些密码函数,需要一些与置乱功能恰恰相反的认证及纠错功能。)
(3)对函数密码的另一个基本要求是稳定的安全性,当对手已经知道了一部分密钥或一部分明文时,整个密码体制不至于因此而立即崩溃。比如,密钥是一个长度为n的比特串,且对手已经知道了其中的k个比特。如果密码体制的安全性过分的依赖于这k 个比特,那就很危险了。反之如果密钥中的n个比特对密码的安全性的贡献是平均的,则无论对手知道的是哪k 个比特,它所面对的破解难度是一样的。特别地,如果密文独立于密钥中的任意k个比特(尽管n个比特的密钥已经完全确定了密文),则这时对手无论得到的是哪k个比特,保密者仍能获得良好的安全性。密钥的这种性质称为相关免疫性或弹性。
(4)为了达到密码算法商业化的目的,人们通常假设钥控加密算法Ek( · )和钥控解密算法Dk( · )是可以公开的;因此要求密码函数Ek( · )和Dk( · )的设计必须满足“唯密钥安全性”;这就是说,密文的保密性仅仅依赖于密钥的保密性,而与算法Ek( · )和Dk( · )的公开与否无关。
2.评价密码体制安全性的量度
简单的说,一个密码体制如果其生成的密文符合以下的两个条件之一,则认为这种加密方案是安全的:
◆破解密文所用的成本超过了被加密信息本身的价值;
◆破解密文所需的时间超过了信息的有效期。
但一般认为评价一个密码体制的安全性有以下的三个准则:
(1)计算安全性(Computational Security)
这种度量涉及到攻破密码体制所需的计算上的努力。如果使用最好的算法攻破一个密码体制需要至少N次操作,这里的N是一个特定的非常大的数字,我们可以定义这个密码体制是计算安全的。问题是没有一个已知的实际的密码体制在这个定义下可以被证明是计算安全的。实际中,人们经常通过几种特定的攻击类型来研究计算上的安全性,例如穷尽密钥搜索攻击。当然对一种类型的攻击是安全的,并不代表对其他类型的攻击也是安全的。
(2)可证明安全性(Provable Security)
另外一种途径是将密码体制的安全性归结为某个已经过深入研究的数学难题。例如可以证明这样一类命题:如果给定的整数是不可分解的,那么给定的密码体制则是不可破解的。我们称这种类型密码体制是可证明安全性的。但应该注意的是,这种途径只是说明了密码体制的安全和另一个问题相关,而并未真正的证明这种密码体制是安全的。这和证明一个问题是NP完全的(NP-Complete)类似:证明给定的问题和其它的NP完全问题的难度是一样的,但并未完全证明这个问题的计算难度。
(3)无条件安全性
这种度量考虑的是对攻击者Eve 的计算量没有限制的时候的安全性。即使是提供了无穷的计算资源,也是无法破解的,这种密码体制被定义为是无条件安全的。
3.密码体制的安全性之一 —— 完善保密性
完善保密性意味着明文随机变量P和密文随机变量C相互独立。它的直观含义是:当攻击者不知道密钥时,知道对应的密文对于估计明文没有任何帮助。这是最强的安全概念。
为了用数学语言描述密码体制的完善保密性,以下假定明文P、密文C、密钥K都是随机变量;P( · )表示概率;P( · | · )表示条件概率;H( · )表示Shannon熵;H( · | · )表示Shannon条件熵;I(· ;· )表示互信息。 由于
C=Ek(P) ; P=Dk(C)
因此,(P,K)唯一确定了C,而(C,K)也唯一确定了P。用信息论的语言就是
H(P | CK)=0 ;H(C | PK)=0 ―――――――――(1.1)
定义1.2-1. 我们称密码体制是完善保密的,如果 I(P ;C)=0 ―――――――――(1.2)
定 理1.2-1. 完善保密的密码体制必然有H(K)≥H(P) ―――――――――(1.3)
证 明: 熵不等式如下所示
H(P)= H(P | C)+ I(P ; C)
= H(P | C) (∵ 式1.2)
≤ H(PK | C)
= H(K | C) + H(P | CK)
= H(K | C) (∵ 式1.1)
≤ H(K)
∴定理1.2-1得证。
关于完善保密性,有如下的注解:
(1)定理1.2-1表明,完善保密的密码体制其密钥的不确定性要不小于明文消息的不确定性,即H(K)≥H(P)。比如,当明文P是n比特长的均匀分布随机变量,为了达到完善保密,密钥K的长度必须至少是n比特长;而且为了用n比特长的密钥达到完善保密,密钥也必须是均匀分布的随机变量。这意味着完善保密的密码体制需要消耗大量的密钥。
(2)完善保密的密码体制是存在的。比如,当明文P=(x1,x2,x3……xn)是n比特长的均匀分布随机变量,密钥K=(k1,k2,k3……kn)也是n比特长的均匀分布随机变量,加密算法为C=P⊕K,其中 ⊕ 为逐比特异或运算。由于 ⊕ 是群运算,故容易看出C是n比特长的均匀分布随机变量,且P和C相互独立。
(3)由概率统计和信息论的知识可以知道,为了实现保密性,通信双方必须在每一次传递秘密消息时,所用的密钥对于攻击者来说都是完全未知的。这就是说,要传递一个新的消息,必须首先更换密钥。这种体制称为“一次一密制”。
完善保密性的密码体制的密钥一般不能用于多次加密。比如在注解(2)的例子中,设两个明文P1和P2都是n比特长的均匀分布随机变量,它们用同一个密钥K进行加密,分别得到密文随机变量C1=P1⊕K 和C2=P2⊕K。设P1、P2及K相互独立,则容易得到:P1、P2、C1相互独立;P1、P2、C2相互独立。但由于P1⊕P2 ≡ C1⊕C2 ,故(C1,C2)与(P1,P2)不相互独立。这说明在本例中,重复使用密钥是得不到完善保密性的。
(4)定理1.2-1引出这样一个问题:对于明文随机变量P,是否存在“最节省密钥”的完善保密的密码体制?即是否存在密码函数Ek( · )和Dk( · ),使得H(K)=H(C)?这实际上是个编码的问题,可以得出的基本结论是:在H(C)→∞的过程中, 总会有完善保密的密码体制使得H(K)任意接近H(P)。
总之,要想实现完善保密性,就必须时时更新密钥;只要有时时更新的密钥,就一定能实现完善保密性。
4.密码体制的安全性之二 —— 计算安全性
一个密钥体制( P,C,K,Ek( · ),Dk( · ) ),如果破译所需的代价太大而难以实现,这个密码体制就称为计算安全的。这里的“代价”通常指计算的复杂度,有时也可以包括经济代价。计算复杂度原本分为时间复杂度和空间复杂度,但由于并行计算技术的发展,在许多情况下可以进行时空转变,故一般不再分为时空,而统称为计算复杂度。计算安全性已经有了多种定义,在这些定义中分别使用了概率图灵机、多项式时间确定性等概念。下面以RSA公钥密码体制作为例子来演示计算安全性。
设p、q是两个大素数,n=p×q 。设e、d是两个正整数,e×d≡1 mod (p-1)×(q-1)。设Alice、 Bob和Eve三人都知道(n ,e),只有Bob知道d,而无人知道(p ,q)。此处(n ,e)为Bob的公钥,d为Bob的私钥。当Alice欲向Bob发送明文消息P时,她计算密文
C ≡ Xe mod n
并将密文C发送给Bob;Bob计算明文
P ≡ Cd mod n
此时Eve能够拦截密文C,但由于不知道素分解n=p×q ,因此没有有效的算法有(n ,e)得到d,虽然(n ,e)唯一确定了d。这样,Eve对明文P的估计近乎于盲目的随机猜测。当然,如果知道素分解n=p×q ,由(p ,q ,e)得到d是很容易的,只需使用欧几里德算法和孙子定理。
5.完善保密性与计算安全性的比较
完善保密性与计算安全性都是密码体制安全性的重要指标,它们之间即相互独立又有密切的关系,以下从不同的角度比较而这之间的关系:
(1)计算安全性的安去强度弱于完善保密性。
(2)从当前看,计算安全性比完善保密性要容易实现得多。具有计算安全性的密码体制允许相同密钥的重复使用,从而减少了密钥协商所需的信息量。
(3)完善保密性的密码体制,由于拥有源源不断的更新密钥,因此不需要精心的设计密码函数,只需要简单的群运算来加密和解密即可。具有计算安全性的密码体制则不然,如果加密算法是简单的群运算C=P Z ,则K=P-1 C。这就是说,当Eve进行已知明文攻击时,只需要一组明文/密文对(P ,C)就解出了密钥。具有计算安全性的密码体制要能抵制已知明文攻击,即当Eve已知k组明文/密文对:(P1 ,C1)、(P2,C2)、……(Pn ,Cn)时,虽然有方程组
Cj=Ek(Xj),其中j=1~k
可能已完全确定了密钥K,但无法将K解出来。这意味着密码函数Ek( · ),Dk( · )需要精心设计。
(4)长期以来由于完善保密性难以实现,故人们在消息保密方面的努力主要集中在计算保密上。近年来形势渐渐有了变化,显示出以下两个特征:①人类的计算能力越来越强,其中包括芯片技术的飞速发展和量子计算机的问世,这一切预示着“计算安全”似乎越来越不可靠。 ②大量有扰信道(比如卫星信道和广播信道)的开通,使得通信伙伴之间共享源源不断的互信息;只要使用消息处理技术,将这些互信息中对手已知的部分去掉,保留并协调对手未知的部分,通信伙伴之间就获得了源源不断的密钥流,因而实现了一次一密,达到“完善保密”。从这个观点来看,完善保密性要比计算安全性优越。