分治与动态规划
待到秋来九月八,我花开后百花杀
- 分治
- 经典二分查找
- 最大部分和
- 大数乘法
- 动态规划
- 取球博弈的升级
- 振兴中华问题的升级
- 城墙刷漆问题
- 环形涂色问题
- 总结
- 分治
- 动态规划
分治
分治法,字面意思是“分而治之”,就是把一个复杂的问题分成两个或多个相同或相似的子问题,再把子问题分成更小的子问题直到最后子问题可以简单地直接求解,原问题的解即子问题的解的合并,这个思想是很多高效算法的基础,例如排序算法(快速排序,归并排序),傅里叶变换(快速傅里叶变换)等。
分治法的基本思想:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
经典二分查找
public class BinariySearch {
static boolean search(int[] arr,int x) {
int L = 0;
int R = arr.length - 1;
while(L<=R) {
int mod = (L+R) / 2;
if(x > mod)
L = mod + 1;
else if(x < mod)
R = mod - 1;
else
return true;
}
return false;
}
public static void main(String[] args) {
int[] a = {1,2,3,4,5,6,7,8,9,0};
System.out.println(search(a,8));
}
}
最大部分和
【问题描述】
数组中整数有正有负
求一连续子段,使得和最大化
例如:
2,4,-7,5,2,-1,2,-4,3
最大连续段:
5,2,-1,2
其最大和为8
思路:我们首先想到的是从第一个开始每个可能的数字组合进行计算和,按照排列组合的思路,的确可行,但同时还需要对比大小,显然这种算法比较耗时。
我们可以考虑使用分治法,将数组分为两部分,那么就会有三种情况:
左边有数字串可能达到最大
右边有数字串可能达到最大
左右两边分别有一部分组合在一起可能达到最大
那么我们就可以,利用递归分治:
public class MaximumSequenceSum {
static int solution(int[] arr,int begin,int end) {
if(end-begin==1)
return arr[begin];
int mod = (begin+end) /2;
int temp_L = solution(arr,begin,mod);
int temp_R = solution(arr,mod,end);
int max_L = 0;
int sum = 0;
for(int i = mod - 1;i>=begin;i--) {
sum += arr[i];
if(sum > max_L)
max_L = sum;
}
int max_R = 0;
sum = 0;
for(int i = mod;i<=end;i++) {
sum += arr[i];
if(sum > max_R)
max_R = sum;
}
int max = max_R + max_L;
if(temp_L > max)
return temp_L;
else if(temp_R > max)
return temp_R;
else
return max;
}
public static void main(String[] args) {
int[] a = {2,4,-7,5,2,-1,2,-4,3};
System.out.println(solution(a,0,a.length-1));
}
}
大数乘法
【问题描述】
用串的形式表示大数的乘法。
即求类似: “23234845847839461464158174814792” * “6457847285617487843234535”
要求结果返回一个串。
思路:按照小学数学乘法规则,我们可以把大数分成左部分和右部分,之后让左部分相乘,右部分相乘,所得的乘积前后拼接,即可得到结果。
当然递归出口,可以选择当大数被截取到足够正常计算的大小即可。
public class bigIntiger {
static String zero(int n) {
if(n == 0)
return "";
if(n == 1)
return "0";
return zero(n/2) + zero(n/2) + zero(n%2);
}
static String bigAdd(String a,String b) {
if(a.length() <= 8 && b.length() <= 8)
return Integer.parseInt(a) + Integer.parseInt(b) + "";
String a_L = "0";
String a_R = a;
if(a.length() > 8) {
a_L = a.substring(0,a.length() - 8);
a_R = a.substring(a.length() - 8);
}
String b_L = "0";
String b_R = b;
if(b.length() > 8) {
b_L = b.substring(0,b.length() - 8);
b_R = b.substring(b.length() - 8);
}
String half_latter = bigAdd(a_R,b_R);
while(half_latter.length() < 8)
half_latter = "0" + half_latter;
if(half_latter.length() > 8)
return bigAdd(bigAdd(a_L,b_L),"1") + half_latter.substring(1);
return bigAdd(a_L,b_L) + half_latter;
}
static String bigMulti(String a,String b) {
if(a.length() <= 4 && b.length() <= 4)
return Integer.parseInt(a) * Integer.parseInt(b) + "";
if(a.length() > 4) {
int mod = a.length() / 2;
String a_L = a.substring(0,mod);
String a_R = a.substring(mod);
return bigAdd(bigMulti(a_L,b)+zero(a_R.length()),bigMulti(a_R,b));
}
return bigMulti(b,a);
}
public static void main(String[] args) {
System.out.println(bigMulti("1234567890987654321666","1234567890123456789555"));
}
}
动态规划
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线.这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问题称为多阶段决策问题。在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化的过程为动态规划方法.
取球博弈的升级
由于在模拟取球游戏时,许多路线和数字都是试验过的并且有结论的方式,那么我们只需要将这些已经有结论的数字保存起来,一但再次遇到不用继续递归计算,可以直接输出胜负。
那么此时一个key—value模型再适合不过了,用map将数字和胜负保存起来,一旦遇到重复的就直接输出。
import java.util.HashMap;
import java.util.Map;
public class TakeBallGame_updata {
static Map map = new HashMap();
static boolean takeBall(int n) {
boolean temp = false;
if(map.get(n) != null)
return (boolean)map.get(n);
if(n >= 1 && takeBall(n-1) == false)
temp = true;
if(n >= 3 && takeBall(n-1) == false)
temp = true;
if(n >= 7 && takeBall(n-1) == false)
temp = true;
if(n >= 8 && takeBall(n-1) == false)
temp = true;
map.put(n, temp);
return temp;
}
public static void main(String[] args) {
map.put(0, true);
for(int i = 1;i<=50;i++) {
System.out.println(i+":"+takeBall(i));
}
}
}
振兴中华问题的升级
对于这个问题同样也可以使用map储存,但在题目要求并无数量上限要求的情况下,使用数组是更简便和时间复杂度降低的方法。
二维数组模拟字符矩阵,根据题目理解只要从右下角开始无论到达横纵边界都可以组成“振兴中华”字符串,那么只需要将边界统一设置为1,那么无论到哪个格子的路线数都可以计算出来。
public class magicString_updata {
public static void main(String[] args) {
int[][] a = new int[100][100];
for(int i = 1;i<100;i++) {
a[i][1] = 1;
a[1][i] = 1;
}
for(int i = 2;i<100;i++) {
for(int j = 2;j<100;j++) {
a[i][j] = a[i-1][j] + a[i][j-1];
}
}
System.out.println(a[5][4]);
}
}
城墙刷漆问题
本题较难,涉及数理推导,解决思路即思考方式,参见:
转载自https://blog.csdn.net/the_ZED/article/details/104724184
自己实现代码:
public class WallPainting {
static long MM = 1000000007;
// 从某个边缘格子开始,到它相邻的边缘格子结束的所有情况
static long fb(int n)
{
if(n==1) return 1;
return fb(n-1) * 2 % MM;
}
// 从某个边缘格子开始的所有情况
static long fa(int n)
{
if(n==1) return 1;
if(n==2) return 6;
return (2 * fa(n-1) + 4 * fa(n-2) + fb(n)) % MM;
}
// 规模为n的问题之中间第i格
static long fk(int i, int n)
{
//return fb(i) * fa(n-i) * 2 * 4 % MM; //相当于镜像互换了
return (fb(i)*fa(n-i)*2 % MM + fb(n-i+1)*fa(i-1)*2 % MM) * 2 % MM;
}
static long f(int n)
{
if(n==1) return 2;
long sum = fa(n) * 4 % MM;
for(int i=2; i<n; i++){
sum = (sum + fk(i,n)) % MM;
}
return sum;
}
public static void main(String[] args)
{
for(int i=1; i<30; i++){
System.out.println(i + ": " + f(i));
}
}
}
第二种:
public class WallPainting {
static long M = 1000000007;
// 从某个边缘格子开始,到它相邻的边缘格子结束的所有情况
static long[] fb = new long[1000];
// 从某个边缘格子开始的所有情况
static long[] fa = new long[1000];
// 规模为n的问题之中间第i格
static long fk(int i, int n)
{
//return fb(i) * fa(n-i) * 2 * 4 % MM; //相当于镜像互换了
return (fb[i]*fa[n-i]*2 % M + fb[n-i+1]*fa[i-1]*2 % M) * 2 % M;
}
static long f(int n)
{
if(n==1) return 2;
long sum = fa[n] * 4 % M;
for(int i=2; i<n; i++){
sum = (sum + fk(i,n)) % M;
}
return sum;
}
public static void main(String[] args)
{
fb[1] = 1;
for(int i=2; i<fb.length; i++){
fb[i] = fb[i-1] * 2 % M;
}
fa[1] = 1;
fa[2] = 6;
for(int i=3; i<fa.length; i++){
fa[i] = (2*fa[i-1] + 4 * fa[i-2] + fb[i]) % M;
}
for(int i=1; i<130; i++){
System.out.println(i + ": " + f(i));
}
}
}
环形涂色问题
【问题描述】如图,组成环形的格子需要涂3种颜色。
它们的编号分别是1~14
相邻的格子不能用相同的颜色。
涂色方案的数目是:24576
当格子数目为50的时候,求涂色方案总数。
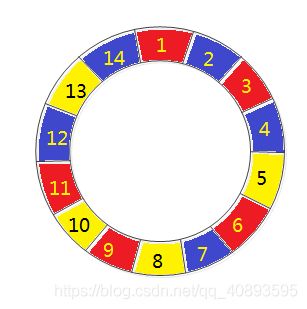
思路:
我们可以假设将环形拆开成条状,对最后一格进行涂色,如图:
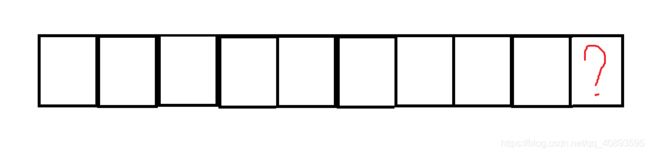
由于在环形中,最后一个与第一个相连,那么最后一个和第一个必然不能一样,在此前提下,那么会有两种情况:
- 倒数第二个和第一个不同,因此最后一个必然只有一种填法。
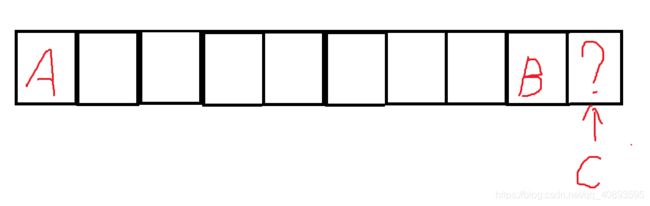
此时,将这个条,依次向内填充,每次将填涂当前看作最后一个,那么就会有F(n-1)种填涂方式。 - 倒数第二个和第一个相同。

此时,最后一位可以有两种填涂方式,此时对于倒数第三格来说,由于倒数第二格和第一格相同,可以将倒数第三格看作最后一格,倒数第二格看作第一格又将形成以一个小环继续上述涂色,因此这种情况下共有2*F(n-1)种方式。
解决方案如下:
public class RingPainting {
static long paint(int n) {
if(n == 1)
return 3;
if(n == 2)
return 6;
if(n == 3)
return 6;
return 2 * paint(n - 2) + paint(n - 1);
}
public static void main(String[] args) {
for(int i = 1;i<30;i++) {
System.out.println(i+": "+paint(i));
}
}
}
但题目要求,50格的数量,显然用递归过大,可以考虑改换为动态规划:
public class RingPainting_updata {
public static void main(String[] args) {
long[] arr = new long[50+20];
arr[1] = 3;
arr[2] = 6;
arr[3] = 6;
for(int i = 4;i<60;i++) {
arr[i] = 2 * arr[i-2] + arr[i-1];
}
for(int i = 1;i<60;i++) {
System.out.println(i+": "+arr[i]);
}
}
}
总结
分治
分治思想主要是将大问题转为小问题的递归主要思想,遇到大数据等无法处理的问题时,我们可以考虑将大问题化小,使用递归解决,最后安排出口实现分治。
动态规划
动态规划是解决递归过多而产生重复计算和时间复杂度较高的问题,解决方式就是记录历史结果,记录方法共有两种:
- 使用map记录n对应结果,形成典型key-value模型,当遇到重复值时直接返回记录结果,不必再进行计算,称为剪枝。
- 使用数组,在要求有限范围内,能够更加高效计算,将每次计算结果保存在数组对应下标下,需要哪个数据输出哪个数据。
但对于类似斐波那契数的问题,仅仅使用的是邻近的两个数,可以用更节省空间的方式,使用3个变量相互交替。
一般动态规划问题都是应用型问题,大多是实际的事件或博弈问题,需要先找出状态转移方程,使用分治等方式先实现递归方法,再考虑动态规划。