非对称加密算法——RSA

三、非对称加密算法 

概念：

非对称加密算法需要两个密钥：公开密钥（publickey）和私有密钥（privatekey）。公开密钥与私有密钥是一对，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫作非对称加密算法。 非对称加密算法实现机密信息交换的基本过程是：甲方生成一对密钥并将其中的一把作为公用密钥向其它方公开；得到该公用密钥的乙方使用该密钥对机密信息进行加密后再发送给甲方；甲方再用自己保存的另一把专用密钥对加密后的信息进行解密。另一方面，甲方可以使用乙方的公钥对机密信息进行签名后再发送给乙方；乙方再用自己的私匙对数据进行验签。甲方只能用其专用密钥解密由其公用密钥加密后的任何信息。 非对称加密算法的保密性比较好，它消除了最终用户交换密钥的需要。

原理图：

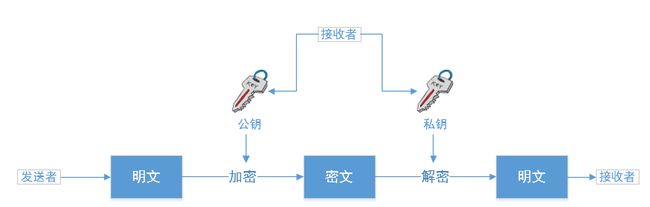
场景1：发送者用接收者的公钥加密，接受者用自己的私钥解密，具体如下图

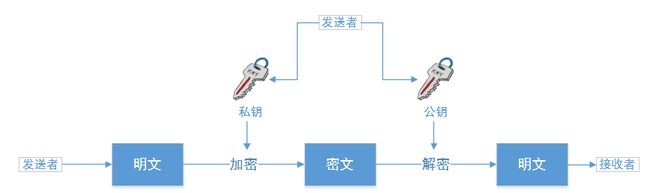
场景2：发送者用自己的私钥加密，接收者用发送者公布的公钥解密，具体如下图

场景3：数字签名中应用，这里暂不进行介绍，后续有相关文章进行详细介绍。

见：http://www.cnblogs.com/yank/p/3533998.html

优点：非对称加密体系不要求通信双方事先传递密钥或有任何约定就能完成保密通信，并且密钥管理方便，可实现防止假冒和抵赖，因此，更适合网络通信中的保密通信要求

主要算法：RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法）。

 

1、RSA

RSA(Rivest-Shamir-Adleman)算法是基于大数不可能被质因数分解假设的公钥体系。简单地说就是找两个很大的质数。一个对外公开的为"公钥"（Public key） ，另一个不告诉任何人，称为"私钥"（Private key）。这两个密钥是互补的，也就是说用公钥加密的密文可以用私钥解密，反过来也一样。

假设用户甲要寄信给用户乙，他们互相知道对方的公钥。甲就用乙的公钥加密邮件寄出，乙收到后就可以用自己的私钥解密出甲的原文。由于别人不知道乙的私钥，所以即使是甲本人也无法解密那封信，这就解决了信件保密的问题。另一方面，由于每个人都知道乙的公钥，他们都可以给乙发信，那么乙怎么确信是不是甲的来信呢？那就要用到基于加密技术的数字签名了。
甲用自己的私钥将签名内容加密，附加在邮件后，再用乙的公钥将整个邮件加密（注意这里的次序，如果先加密再签名的话，别人可以将签名去掉后签上自己的签名，从而篡改了签名）。这样这份密文被乙收到以后，乙用自己的私钥将邮件解密，得到甲的原文和数字签名，然后用甲的公钥解密签名，这样一来就可以确保两方面的安全了。

加密：

        /// 

        /// RSA加密
        /// 
        /// 明文
        /// 公钥
        /// 密文字符串
        public static string EncryptByRSA(string plaintext, string publicKey)
        {           
            UnicodeEncoding ByteConverter = new UnicodeEncoding();         
            byte[] dataToEncrypt = ByteConverter.GetBytes(plaintext);
            using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider())
            {
                RSA.FromXmlString(publicKey);
                byte[] encryptedData = RSA.Encrypt(dataToEncrypt, false);
                return Convert.ToBase64String(encryptedData);
            }
        }

 

解密：

        /// 

        /// RSA解密
        /// 
        /// 密文
        /// 私钥
        /// 明文字符串
        public static string DecryptByRSA(string ciphertext, string privateKey)
        {
            UnicodeEncoding byteConverter = new UnicodeEncoding();
            using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider())
            {
                RSA.FromXmlString(privateKey);
                byte[] encryptedData = Convert.FromBase64String(ciphertext);
                byte[] decryptedData = RSA.Decrypt(encryptedData, false);
                return byteConverter.GetString(decryptedData);
            }
        }

 

所有案例，见测试DEMO

源码地址：http://files.cnblogs.com/yank/EncriptSample.zip

 

RSA加密解密及RSA签名和验证

1.RSA加密解密：
　(1)获取密钥，这里是产生密钥，实际应用中可以从各种存储介质上读取密钥 (2)加密 (3)解密
2.RSA签名和验证
　(1)获取密钥，这里是产生密钥，实际应用中可以从各种存储介质上读取密钥 (2)获取待签名的Hash码 (3)获取签名的字符串 (4)验证

3.公钥与私钥的理解：
　(1)私钥用来进行解密和签名，是给自己用的。
　(2)公钥由本人公开，用于加密和验证签名，是给别人用的。
   (3)当该用户发送文件时，用私钥签名，别人用他给的公钥验证签名，可以保证该信息是由他发送的。当该用户接受文件时，别人用他的公钥加密，他用私钥解密，可以保证该信息只能由他接收到。

 

 

节选自：https://www.cnblogs.com/yank/p/3528548.html

https://www.cnblogs.com/sydeveloper/archive/2012/08/11/2633624.html