第1天:网易2018年校园招聘NLP算法工程师笔试试卷分析
前言
由于剑指offer题目全部刷完了,由于现在就开始秋招了,今天早上借此机会做了一份2018年网易秋招的NLP工程师笔试题,大家有兴趣的话可以做一下,检验自己最近的复习成果。整体而言,感觉网易的这套试卷比较难,尤其是三道编程题,都感觉不简单,难度偏上。这份题一共有九道题,其中五道是单选题,三道编程题,一道是问答题。五道单选题,分别考察了机器学习算法(凸集、LDA、几种熵的区别)、编程语言、数据结构中的完全二叉树。三道编程题均是实际问题,分别考察了我们对贪心算法、找规律以及动态规划的思想,要在短暂的时间写出这三道题的代码是很不容易的,要比我们平常练习的剑指Offer难。最后就是一道问答题,主要让我们回答我们做的一个NLP的项目,大致说一下自己负责的部分以及遇到的问题和解决的方案。接下来,我们详细的分析这九道题。
试题分析
一、选择题
1、以下集合是凸集的是(A)

【分析】 本题主要考察我们对凸集概念的掌握情况。我们回顾一下凸集的定义:我们定义一个集合是凸的,当且仅当任意x,y∈C且θ∈R,0⩽θ⩽1,

实际上,这意味着如果我们在集合C中取任意两个元素,在这两个元素之间画一条直线,那么这条直线上的每一点都属于C。图1显示了一个示例的一个凸和一个非凸集。其中点
θx+(1-θ)y被称作点集x,y的凸性组合(convex combination)。

而在本题中,选项A是线性函数,是凸集。B是圆,很明显不符合。C是圆的外面部分,也不满足凸集的概念。D只是(1,1)点更不是。因此本题故选A。更多凸优化学习的相关知识还请大家看此文章。
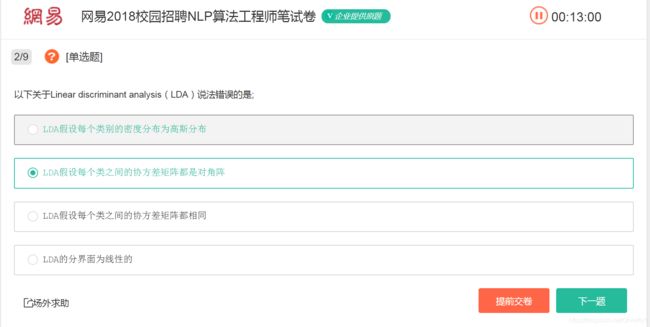
2、以下关于Linear discriminant analysis(LDA)说法错误的是;(B)
【分析】 本题主要考察LDA的相关知识。Linear Discriminant Analysis是Ronald Fisher于1936年提出的方法,因此又叫做Fisher’s linear discriminant。LDA的思想:最大化类间方差与最小化类内方差,即减少分类内部之间的差异,而扩大不同分类之间的差异。其实PCA选择样本点投影具有最大方差的方向,LDA选择分类性能最好的方向。

但是,使用LDA的一些限制:
1、LDA至多可生成C-1维子空间。C为类别数。LDA降维后的维度区间在[1,C-1],与原始特征数n无关,对于二值分类,最多投影到1维。
2、LDA不适合对非高斯分布样本进行降维。
3、LDA在样本分类信息依赖方差而不是均值时,效果不好。
根据上述对LDA的描述,我们可知B选项是错误的,它并不是对角阵。具体详细的内容请查看该文章。因此最后答案是选B。
3、在以下示意图中, 交集部分可以表示哪个统计量( C )
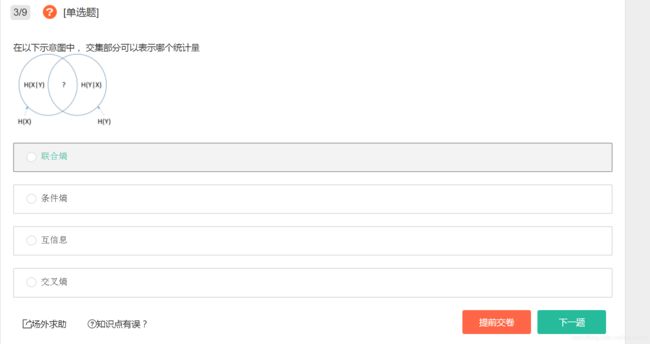
【分析】 本题主要考察的是各种熵的对比。
- 信息熵:左边的椭圆代表 H(X),右边的椭圆代表H(Y)。
- 互信息(信息增益):是信息熵的交集,即中间重合的部分就是 I(X,Y)
- 联合熵:是信息熵的并集,两个椭圆的并就是 H(X,Y)
- 条件熵:是差集。左边的椭圆去掉重合部分就是 H(X|Y),右边的椭圆去掉重合部分就是H(Y|X)
还可以看出:
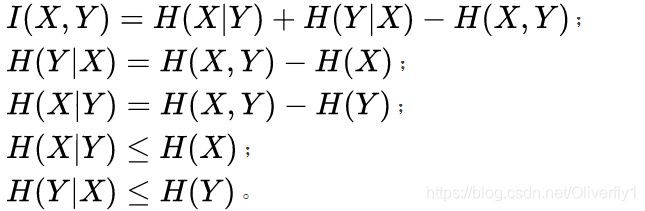
因此,通过上图以及我们提到的几种熵相对应的位置可知,本题交集的部分是互信息。因此选C。详细几种熵的定义可以阅读该文章。
4、某棵完全二叉树上有555个节点,则该二叉树的叶子节点数为©
【分析】 本题主要考察数据结构中完全二叉树的相关知识。这种题目在笔试中经常出现的,考察我们对完全二叉树的理解。具体的解答过程如下:

5、下面关于dynamic_cast说法错误的有?©

【分析】 本题主要考察我们对C++编程语言中dynamic_cast的理解与掌握。dynamic_cast是将一个基类对象指针(或引用)转换到继承类指针,dynamic_cast会根据基类指针是否真正指向继承类指针来做相应处理。dynamic_cast运算符它涉及到编译器的属性设置,而且牵扯到的面向对象的多态性跟程序运行时的状态也有关系,所以不能完全的使用传统的转换方式来替代。但是也因此它是最常用,最不可缺少的一个运算符。与static_cast一样,dynamic_cast的转换也需要目标类型和源对象有一定的关系:继承关系。 更准确的说,dynamic_cast是用来检查两者是否有继承关系。因此该运算符实际上只接受基于类对象的指针和引用的类转换。从这个方面来看,似乎dynamic_cast又和reinterpret_cast是一致的,但实际上,它们还是存在着很大的差别。dynamic_cast运算符的主要用途:将基类的指针或引用安全地转换成派生类的指针或引用,并用派生类的指针或引用调用非虚函数。如果是基类指针或引用调用的是虚函数无需转换就能在运行时调用派生类的虚函数。前提条件:当我们将dynamic_cast用于某种类型的指针或引用时,只有该类型含有虚函数时,才能进行这种转换。否则,编译器会报错。
指针类型的dynamic_cast: 如果一条dynamic_cast语句的转换目标是指针类型并且转换失败了,会返回一个空指针,则判断条件为0,即为false;如果转换成功,指针为非空,则判断条件为非零,即true。注意:我们可以对一个空指针执行dynamic_cast,结果是所需类型的空指针。引用类型的dynamic_cast: 引用类型的dynamic_cast和指针类型的dynamic_cast在表示错误发生的方式上略有不同。因为不存在空引用,所以对于引用类型来说无法使用与指针类型完全相同的错误报告策略。当对引用类型转换失败时,程序抛出一个名为std::bad_cast的异常,该异常定义在typeinfo标准库头文件中。
因此,根据上述我们对dynamic_cast相关知识的介绍,故选C。
二、编程题
1、题目描述:
魔法王国一共有n个城市,编号为0~n-1号,n个城市之间的道路连接起来恰好构成一棵树。
小易现在在0号城市,每次行动小易会从当前所在的城市走到与其相邻的一个城市,小易最多能行动L次。
如果小易到达过某个城市就视为小易游历过这个城市了,小易现在要制定好的旅游计划使他能游历最多的城市,请你帮他计算一下他最多能游历过多少个城市(注意0号城市已经游历了,游历过的城市不重复计算)。
具体要求:
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
输入包括两行,第一行包括两个正整数n(2 ≤ n ≤ 50)和L(1 ≤ L ≤ 100),表示城市个数和小易能行动的次数。
第二行包括n-1个整数parent[i](0 ≤ parent[i] ≤ i), 对于每个合法的i(0 ≤ i ≤ n - 2),在(i+1)号城市和parent[i]间有一条道路连接。
输出描述:
输出一个整数,表示小易最多能游历的城市数量。
输入例子1:
5 2
0 1 2 3
输出例子1:
3
具体思路
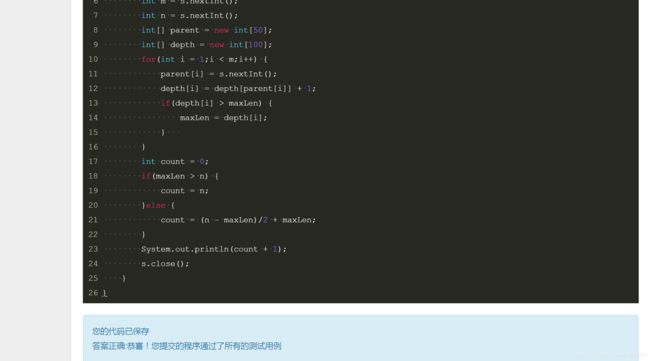
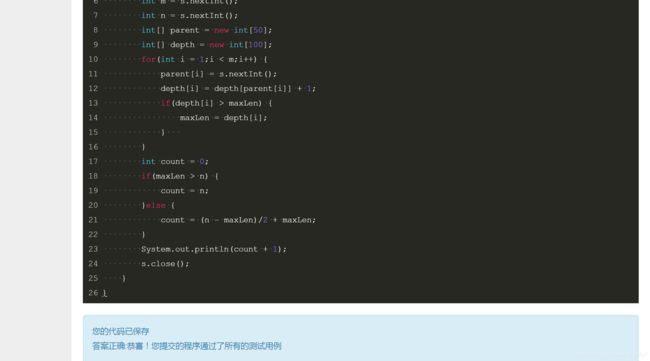
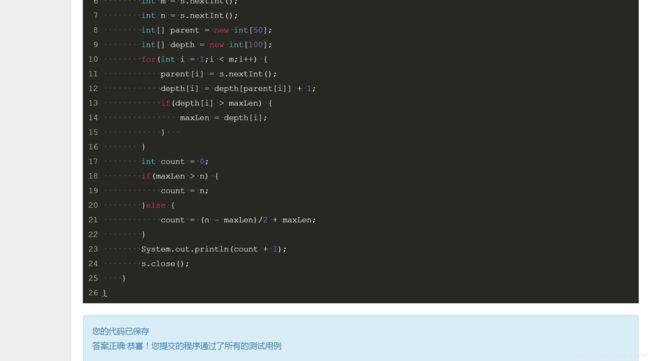
本题说白了就是考察的贪心算法。就小易能行动的次数来讨论,当小易的行动次数小于树的最大深度的时候,那么小易此时能访问的城市数量就等于行动次数 + 1 。当小易的行动次数大于树的最大深度时,则不能从最大深度的分支一直走下去。从最坏的角度来看,如果最大深度的分支没有其他分支,只有回到根结点处找另一个分支,这样损失的行动次数过多,经过的城市数量也不能达到最大,所以在这种情况下,如果要保证经过的城市最多,最长的分支是必须走完的,那么多余的行动次数可以走其他的分支,假设行动次数为n,最长分支为maxLen,那么多余的行动次数为n-maxLen,考虑到来回的问题那么多余的行动次数能经过的城市为(n - maxLen)/2,所以经过的城市数量为maxLen + (n - maxLen)/2 + 1 。具体用java实现如下:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int maxLen = 0;
int m = s.nextInt();
int n = s.nextInt();
int[] parent = new int[50];
int[] depth = new int[100];
for(int i = 1;i < m;i++) {
parent[i] = s.nextInt();
depth[i] = depth[parent[i]] + 1;
if(depth[i] > maxLen) {
maxLen = depth[i];
}
}
int count = 0;
if(maxLen > n) {
count = n;
}else {
count = (n - maxLen)/2 + maxLen;
}
System.out.println(count + 1);
s.close();
}
}
N, L = map(int, input().split())
parents = [int(i) for i in input().split()]
nodes_depth = [0] * N
for i in range(N-2):
nodes_depth[i+1] = nodes_depth[parents[i]] + 1
max_depth = max(nodes_depth)
if L <= max_depth:
max_cities = L + 1
else:
max_cities = max_depth + ((L - max_depth) // 2) + 1
if max_cities <= N:
print(max_cities)
else:
print(N)
小易有一个长度为N的正整数数列A = {A[1], A[2], A[3]…, A[N]}。
牛博士给小易出了一个难题:
对数列A进行重新排列,使数列A满足所有的A[i] * A[i + 1](1 ≤ i ≤ N - 1)都是4的倍数。
小易现在需要判断一个数列是否可以重排之后满足牛博士的要求。
具体要求:
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
输入的第一行为数列的个数t(1 ≤ t ≤ 10),
接下来每两行描述一个数列A,第一行为数列长度n(1 ≤ n ≤ 10^5)
第二行为n个正整数A[i](1 ≤ A[i] ≤ 10^9)
输出描述:
对于每个数列输出一行表示是否可以满足牛博士要求,如果可以输出Yes,否则输出No。
输入例子1:
2
3
1 10 100
4
1 2 3 4
输出例子1:
Yes
No
具体思路
本题其实就是找规律。
① 最简单的实现:考虑当前数列的所有排列,根据判断条件(A[i]A[i+1])%4是否等于0判断该数列是否满足;
② 对满足和不满足的数列进行分析:
a.如果数列中不存在是2的倍数的数,那么最终满足的数列应该类似于(1 4 3)形式,即将4放在中间,其他数放在两边(此时的判断条件为:count_2==0 && count_4>=count_others-1,其中count代表每类数在数列中出现的次数);
b.如果数列中存在是2的倍数的数,那么最终满足的数列应该类似于(1 4 2,2 2 4)形式,即将4放在中间,其他数放在两边(此时的判断条件为:count_2!=0 && count_4>=count_others,其中count代表每类数在数列中出现的次数);
存在的问题:为什么不考虑将2也当做和1,3一样的数来处理?
分析:由于存在2 2与2 8 6等的情况存在,此时没有4也同样可以完成题目要求;具体用java将其实现:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(sc.hasNext()){
int n = sc.nextInt();
int two = 0;
int four = 0;
for(int i=0; i<n; i++){
int a = sc.nextInt();
if(a%4 == 0)
four++;
else if(a%2 == 0)
two++;
}
if(four >= n-four-two)
System.out.println("Yes");
else
System.out.println("No");
}
sc.close();
}
}
具体效果图如图所示:

当然我们也可以用于python来实现该题,具体实现如下:
t = int(input())
ns = []
arrays = []
for each in range(t):
ns.append(int(input()))
arrays.append([i for i in map(int, input().split())])
count = 0
results = []
while count < t:
n = ns[count]
array = arrays[count]
fours = 0
twos = 0
others = 0
for each in array:
if each % 4 == 0:
fours += 1
elif each % 2 == 0:
twos += 1
else:
others += 1
if twos == 0:
if fours >= n // 2:
results.append('Yes')
else:
results.append('No')
else:
if fours >= others:
results.append('Yes')
else:
results.append('No')
count += 1
for each in results:
print(each)
3、题目描述:
小易正在玩一款新出的射击游戏,这个射击游戏在一个二维平面进行,小易在坐标原点(0,0),平面上有n只怪物,每个怪物有所在的坐标(x[i], y[i])。小易进行一次射击会把x轴和y轴上(包含坐标原点)的怪物一次性消灭。
小易是这个游戏的VIP玩家,他拥有两项特权操作:
1、让平面内的所有怪物同时向任意同一方向移动任意同一距离
2、让平面内的所有怪物同时对于小易(0,0)旋转任意同一角度
小易要进行一次射击。小易在进行射击前,可以使用这两项特权操作任意次。
小易想知道在他射击的时候最多可以同时消灭多少只怪物,请你帮帮小易。
如样例所示:
所有点对于坐标原点(0,0)顺时针或者逆时针旋转45°,可以让所有点都在坐标轴上,所以5个怪物都可以消灭。
具体要求:
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
输入包括三行。
第一行中有一个正整数n(1 ≤ n ≤ 50),表示平面内的怪物数量。
第二行包括n个整数x[i](-1,000,000 ≤ x[i] ≤ 1,000,000),表示每只怪物所在坐标的横坐标,以空格分割。
第二行包括n个整数y[i](-1,000,000 ≤ y[i] ≤ 1,000,000),表示每只怪物所在坐标的纵坐标,以空格分割。
输出描述:
输出一个整数表示小易最多能消灭多少只怪物。
输入例子1:
5
0 -1 1 1 -1
0 -1 -1 1 1
输出例子1:
5
具体思路
寻找垂直线。 利用已知的点,寻找两条相互垂直的直线,使落在这条直线上的点最多,点的数量就是小易最多能消灭的怪物数量, 先选出两个点连成一条直线,然后选出第三个点,这第三个点不能和前两个点重合,也不能在前两个点连成的直线上。之后去找第四个点,如果第四个点在前两个点所连成的直线上,或者和第三个点组成的直线与上一条直线垂直,则记数变量加1,遍历完后所有情况后,输出最大的记数变量即可。具体我们用java可以实现:
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] x = new int[n];
int[] y = new int[n];
for(int i=0;i < n;i++){
x[i] = sc.nextInt();
}
for(int i=0;i < n;i++){
y[i] = sc.nextInt();
}
int[] slope = new int[n*n];
int[] verticalSlope = new int[n*n];
int s=0;
for(int j=0;j < n;j++){
for(int k=j+1; k < n;k++){
if(x[j]-x[k] != 0 && y[j]-y[k] != 0){
slope[s] = (x[j]-x[k])/(y[j]-y[k]);
if(slope[s] != 0){
verticalSlope[s] = -1*(1/slope[s]);
s++;
}
}
}
}
int b1 = 0;
int b2 = 0;
int counth = 0;
int countv = 0;
int intersection = 0;
int temp1=0;
int temp2=0;
for(int u=0;u<s;u++){
for(int i=0;i<n;i++){
b1 = slope[u]*x[i]-y[i];
for(int j=0;j<n;j++){
b2 = verticalSlope[u]*x[j]-y[j];
for(int k=0;k<n;k++){
if(y[k] == slope[u]*x[k]-b1){
counth++;
}
if(y[k] == verticalSlope[u]*x[k]-b2){
countv++;
}
if(y[k] == slope[u]*x[k]-b1 && y[k] == verticalSlope[u]*x[k]-b2){
intersection++;
}
}
temp1 = counth+countv-intersection;
counth = 0;
countv = 0;
intersection = 0;
if(temp1 > temp2){
temp2 = temp1;
}
}
}
}
int xValue = 0;
int yValue = 0;
int counth2 = 0;
int countv2 = 0;
int intersection2 = 0;
int temp3 = 0;
int temp4 = 0;
for(int u=0;u<n;u++){
for(int i=0;i<n;i++){
xValue = x[u];
yValue = y[i];
for(int j=0;j<n;j++){
if(x[j] == xValue){
counth2++;
}
if(y[j] == yValue){
countv2++;
}
if(x[j] == xValue && y[j] == yValue){
intersection2++;
}
}
temp3 = counth2+countv2-intersection2;
counth2 = 0;
countv2 = 0;
intersection2 = 0;
if(temp3 > temp4){
temp4 = temp3;
}
}
}
if(temp4 > temp2){
temp2 = temp4;
}
System.out.println(temp2);
}
}
具体效果如图所示:
当然,我们也可以用python实现。具体实现如下:
n = int(input())
x,y = list(map(int, input().split())),list(map(int, input().split()))
max_n = 0
if n < 4:
max_n = n
for i in range(n-3):
for j in range(i+1,n-2):
if i != j:
X1 = x[j] - x[i]
Y1 = y[j] - y[i]
for k in range(i+2,n-1):
if (k != i)and(k != j):
count = 3
for l in range(i+3,n):
if (l != i)and(l != j)and(l != k):
X2 = x[l] - x[k]
Y2 = y[l] - y[k]
X3 = x[l] - x[i]
Y3 = y[l] - y[i]
if (X1*X2+Y1*Y2==0) or (X1*Y3==X3*Y1):
count += 1
if (count > max_n):
max_n = count
print (max_n)
三、问答题
题目描述
请言简意赅地描述一个你所参与的NLP相关项目,包括项目的目标(需要解决的问题)以及系统架构,然后详述一个你最熟悉的模块。
如果上述模块是采用传统的机器学习算法(LR,GBDT,SVM等),请你结合应用谈谈你是如何设计和选择特征的;如果采用的是深度学习方法,请你说明此项目中使用的深度学习算法具有什么样的优势?
在该项目中是否使用某些开源的工具或者框架,对比同类工具和框架他们具有什么特点?
描述你在参与项目中遇到的主要困难以及你的解决办法。
注意:本题暂不支持系统判断,可在交卷后查看参考答案。
以下只是我个人答案:
项目名称:关键词搜索系统的实现
项目目标:用NLP中的NLTK语料库对关键词进行搜索
用到的架构:前端是用node.js下的Vue以及HTML为主作为开发,后端是利用流行的SSM框架作为后端的。并且利用redis作为数据的缓存。
负责的模块:对预料库中的关键词进行提取,通过建立模型来达到其准确率。本人在主题词提取中用到了Word2vec以及LDA,并且用到了LSTM对其关键词的模型进行训练。其准确率高达99.5%。在这个项目中,用RNN中的LSTM算法,使其独有的双循环门得到了充分的利用,并且激活函数用到了BRELU,用adam作为优化器,用mse作为损失函数。
主要的困难:在建模的时候,测试集上的效果比较差,只能达到85.23%,可是在训练集竟然能到达到99.36%,也就是我们常见的过拟合问题。最后的效果提升的很明显。
总结
通过对公司真题的解答发现,公司的题目还是整体很注重基础算法的,并且考察的比较全面,着重考察的是我们对数据结构与算法的掌握程度,和我们平常练习的有所差别,我们还得继续努力,掌握好每个知识点。并且要学会学以致用。秋招马上启动,该开始刷题了,好好准备,希望2021届毕业的我们都能有一份满意的Offer,Good Luck!!!