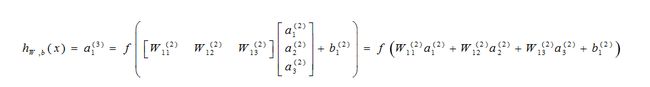参考:
1. Stanford前向传播神经网络Wiki
2. Stanford后向传播Wiki
3. 神经网络CSDN blog
4. 感知器
5. 线性规划
6. Logistic回归模型
内容:
1. ANNs又称连接模型(connection model),它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的数学模型。它是由一系列简单的单元相互密集连接构成的,其中每一个单元有一定数量的实值输入,并产生单一的实数值输出。
2. m-of-n函数:要使函数输出为真,那么感知器的n个输入中至少有m个必须为真。OR函数相当于m=1,AND函数相当于m=n。
3. 某种类型的ANN系统是以被称为感知器(perception)的单元为基础的。感知器是以一个实数值向量作为输入,计算这些输入的线性组合,然后如果结果大于某个阈值,就输出1,否则输出-1。
这里-w0就是阈值。这里的学习任务就是权向量的值。
图1 单输出神经网络
图2 多输出神经网络
4. 学习任务算法:感知器法则与delta法则。
感知器法则(前提是训练样例线性可分):为得到可接受的权向量,从随机的权值开始,然后反复地应用这个感知器到每个训练样例,只要它误分类样例就修改感知器的权值。重复这个过程,直到感知器正确分类所有的训练样例。
其中,t是当前训练样例的目标输出,o是感知器的输出,η是一个正的常数称为学习速率(learning rate)。
delta法则(线性不可分也可以):使用梯度下降(gradient descent)来搜索可能的权向量的假设空间,以找到最佳拟合训练样例的权向量。
把delta训练法则理解为训练一个无阈值的感知器,也就是一个线性单元,它的输出如下:
假设(权向量)相对于训练样例的训练误差如下:
其中,D是训练样例集合,td是训练样例d的目标输出,od是线性单元对训练样例d的输出。这里的1/2是为了抵消求导后的2。其梯度如下:
当梯度被解释为权空间的一个向量时,它确定了是E最陡峭上升的方向。
5. 单个感知器只能表示线性决策面,而反向传播算法所学习的多层网络能表示非线性曲面。多层网络需要这样一种单元,它的输出是输入的非线性函数,并且输出是输入的可微函数。比如sigmoid单元,它的输出如下:
误差E如下:
其中,outputs是网络输出单元的集合,tkd和okd是与训练样例d和第k个输出单元相关的输出值。
➊ 网络中每个结点被赋予一个序号,这里的“结点”要么是网络的输入,要么是网络中某个单元的输出。
➋ xji表示结点i到单元j的输入,wji表示对应的权值。
对于网路的每个输出单元k,它的误差项为:
对于网络的每个隐藏单元h,它的误差项为:
权值更新: