剑指offer——数学类问题集合(Leetcode)
面试题10- I. 斐波那契数列
题目
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
输入:n = 5
输出:5
法一:直接按照递推式写即可。
class Solution {
public int fib(int n) {
int a=0,b=1;
for(int i=1;i<=n;i++){
int sum=(a+b)%1000000007;
b=a;
a=sum;
}
return a;
}
}
法二:矩阵快速幂
快速幂+矩阵快速幂参考博客
注意long long数据类型,防止溢出。
class Solution {
public:
typedef long long ll;
const int mod=1000000007;
struct Matrix{
ll a[2][2];
Matrix(){
memset(a,0,sizeof(a));
}
};
Matrix mul(Matrix A,Matrix B){
Matrix C;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%mod;
}
}
}
return C;
}
Matrix pow_mod(Matrix A,int n){
Matrix B;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
B.a[i][j]=i==j?1:0;
while(n)//快速幂
{
if(n&1) B=mul(B,A);
A=mul(A,A);
n=n>>1;
}
return B;
}
int fib(int n) {
if(n==0) return 0;
Matrix A;
A.a[0][0]=A.a[0][1]=A.a[1][0]=1;//初始化T矩阵
A=pow_mod(A,n-1);
return A.a[0][0];
}
};
面试题10- II. 青蛙跳台阶问题
题目
和I的斐波那契数列完全一致,只是定义F(0)=1.
class Solution {
public:
typedef long long ll;
const int mod=1000000007;
struct Matrix{
ll a[2][2];
Matrix(){
memset(a,0,sizeof(a));
}
};
Matrix mul(Matrix A,Matrix B){
Matrix C;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%mod;
}
}
}
return C;
}
Matrix pow_mod(Matrix A,int n){
Matrix B;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
B.a[i][j]=i==j?1:0;
while(n)//快速幂
{
if(n&1) B=mul(B,A);
A=mul(A,A);
n=n>>1;
}
return B;
}
int numWays(int n) {
if(n==0) return 1;
Matrix A;
A.a[0][0]=A.a[0][1]=A.a[1][0]=1;//初始化T矩阵
A=pow_mod(A,n-1);
return (A.a[0][0]+A.a[0][1])%mod;
}
};
面试题14- I. 剪绳子
题目
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
采用数学推导。优秀题解
关键两个步骤:
- 利用算术几何均值不等式,得到结论1:当所有绳段长度相等时,乘积最大
- 在结论一的推导下,对原公式求导,得到取得最大值的极值点为3。得到结论2:最优的绳段长度为 3。
注意点:切割可能不会是刚好按照3的倍数切分的,那么最后一段的长度可能是1,2。对这两类情况要单独讨论:
- 如果是2,保留不再切分;
- 如果是1,将前面的一个3合并,转化成2+2切分,因为31>22.
class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
面试题14- II. 剪绳子 II
题目
在剪绳子I的背景下,加上了大数越界情况下的求余问题,即之前的3a,不能再直接使用pow求解,使用快速幂进行求解即可。
这里一定注意数据类型,要用long;该有的括号一定不能少,比如最后的(sum*3%mod)。
class Solution {
int mod=1000000007;
public int cuttingRope(int n) {
if(n<=3) return n-1;
int b=n%3,a=n/3-1;
//快速幂计算3^(a-1)
long sum=1,x=3;
while(a>0){
if((a&1)!=0){
sum=(sum*x)%mod;
}
x=(x*x)%mod;
a>>=1;
}
if(b==0) return (int)(sum*3%mod);
if(b==1) return (int)(sum*4%mod);
return (int)(sum*6%mod);
}
}
python太强了,Python 中的变量取值范围由系统内存大小决定(无限大),因此在 Python 中其实不用考虑大数越界问题。还是自由地和上面一题一样就OK了~
class Solution:
def cuttingRope(self, n: int) -> int:
if n<=3:
return n-1;
mod=1000000007
a,b=n//3,n%3
if b == 0: return 3 ** a % mod
if b == 1: return 3 ** (a - 1) * 4 % mod
return 3 ** a * 2 % mod
面试题15. 二进制中1的个数
题目
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
方法一:逐位判断
最平常的方法。
但是这里要注意,如果使用第一种移动方法,由于n可能是负数,那么本题要求把数字 n 看作无符号数,因此使用 无符号右移 操作。JAVA中无符号右移是>>>。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int cnt=0;
while(n!=0){
if((n&1)!=0){
cnt++;
}
n>>>=1;
}
return cnt;
}
}
也可以直接判断后31位,不判断符号位。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int cnt=0;
for(int i=0;i<32;i++){
if((n&(1<<i))!=0){
// System.out.println(n&(1<
cnt++;
}
}
return cnt;
}
}
方法二:巧用 n&(n−1)
(n−1) 解析: 二进制数字 n 最右边的 1 变成 0 ,此 1 右边的 0 都变成 1 。
n&(n−1) 解析: 二进制数字 n 最右边的 1 变成 0 ,其余不变。
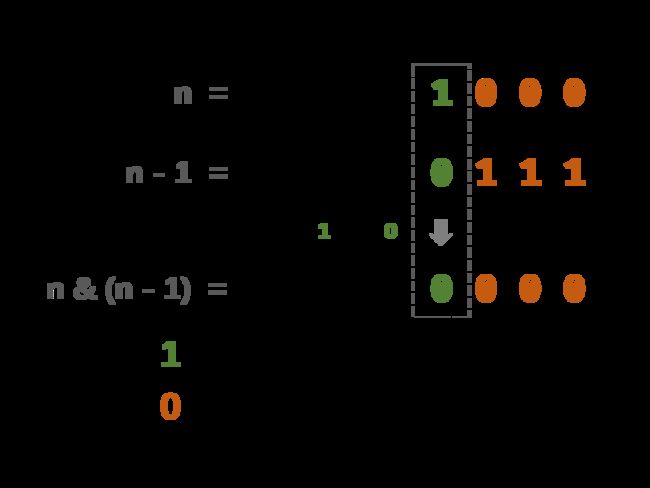
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res++;
n &= n - 1;
}
return res;
}
}
面试题16. 数值的整数次方
题目
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
输入: 2.00000, 10
输出: 1024.00000
输入: 2.00000, -2
输出: 0.25000
其实还是快速幂的问题。不要被题目中的double吓到。
出错点:在处理次方数为负数的情况,需要将a(-b)转化为(1/a)b,因此对负数需要做b=-b的操作。java 代码中 int32 变量 n∈[−2147483648,2147483647] ,因此当n=−2147483648 时执行n=−n 会因越界而赋值出错。解决方法是先将n存入 long 变量 b,后面用 b操作即可。
和上一题一样,一定要注意java中的负数问题。
class Solution {
public double myPow(double x, int n) {
long k=n;
if(n<0){
x=1/x;
k=-k;
}
double ans=1.0;
while(k>0){
if((k&1)!=0){
ans=ans*x;
}
x=x*x;
k>>=1;
}
return ans;
}
}
面试题17. 打印从1到最大的n位数
题目
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]
快速幂即可,一共要打印出[1,10n]个数,那么用快速幂求解10n。这一题的感受是,对于快速幂的使用非常灵活,往后对于带有幂次方的题目一定要敏感,及时考虑到快速幂的应用。
class Solution {
public int[] printNumbers(int n) {
if(n <= 0) return new int[0];
int result = 1;
int x = 10;
//该题考查快速幂;
while(n != 0){
if((n & 1) == 1){
result *= x;
}
n >>= 1;
x *= x;
}
int len = result - 1;
int[]array = new int[len];
for(int i = 0;i < len;i++){
array[i] = i + 1;
}
return array;
}
}
面试题46. 把数字翻译成字符串
题目
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", “bwfi”, “bczi”, “mcfi"和"mzi”
方法一:DP
很显然的dp公式:
dp[i]= dp[i-1]+ str[i-1,i]<=25?dp[i-2]:0
dp[i]表示到第i个字符为止,一共的翻译方法。
dp数组实现:
class Solution {
public:
int translateNum(int num) {
if(num<10) return 1;
string nums=to_string(num);
int len=nums.length();
int dp[len+1];
dp[0]=1;dp[1]=1;
for(int i=2;i<=len;i++){
dp[i]=dp[i-1];
if((nums[i-2]-'0')!=0&&(nums[i-2]-'0')*10+(nums[i-1]-'0')<=25){
dp[i]+=dp[i-2];
}
}
return dp[len];
}
};
滚动数组实现:
class Solution {
public:
int translateNum(int num) {
string src = to_string(num);
int p = 0, q = 0, r = 1;
for (int i = 0; i < src.size(); ++i) {
p = q;
q = r;
r = 0;
r += q;
if (i == 0) {
continue;
}
auto pre = src.substr(i - 1, 2);
if (pre <= "25" && pre >= "10") {
r += p;
}
}
return r;
}
};
面试题38. 字符串的排列
题目
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
输入:s = “abc”
输出:[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]
- 偷懒方法:直接c++中next_permutation
class Solution {
public:
vector<string> permutation(string s) {
vector<string> ans;
sort(s.begin(),s.end());
do{
ans.push_back(s);
}while( next_permutation(s.begin(),s.end()) );
return ans;
}
};
- DFS思想。
注意去重思想。
class Solution {
public:
vector<string> res;
int len;
string s;
vector<string> permutation(string ss) {
s=ss;
len=s.length();
dfs(0);
return res;
}
void dfs(int x){
if(x==len-1){
res.push_back(s);
return;
}
set<char> st;
for(int i=x;i<len;i++){
if(st.count(s[i])) continue;
st.insert(s[i]);
swapString(x,i);
dfs(x+1);
swapString(x,i);
}
}
void swapString(int i,int x){
char tmp=s[i];
s[i]=s[x];
s[x]=tmp;
}
};
面试题40. 最小的k个数
题目
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
方法一:堆
我们用一个大根堆实时维护数组的前 k 小值。首先将前 k个数插入大根堆中,随后从第 k+1个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。
- C++ 语言中的堆(即优先队列)为大根堆,我们可以这么做。
- Java 的 PriorityQueue 默认是小顶堆,添加 comparator 参数使其变成最大。
- Python 语言中的对为小根堆,因此我们要对数组中所有的数取其相反数,才能使用小根堆维护前 k 小值。
算法的复杂度分析:
- 由于使用了一个大小为 k 的堆,空间复杂度为O(k);
- 入堆和出堆操作的时间复杂度均为O(logk),每个元素都需要进行一次入堆操作,故算法的时间复杂度为O(nlogk)。
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res(k,0);
if(k==0) return res;
priority_queue<int> qn;
for(int i=0;i<k;i++){
qn.push(arr[i]);
}
int len=arr.size();
for(int i=k;i<len;i++){
if(arr[i]<qn.top()){
qn.pop();
qn.push(arr[i]);
}
}
for(int i=0;i<k;i++){
res[i]=qn.top();qn.pop();
}
return res;
}
};
方法二:快速选择
这个题解对这里的快速选择解释的蛮好的。
“查找第 k 大的元素”是一类算法问题,称为选择问题。找第 k 大的数,或者找前 k 大的数,有一个经典的 quick select(快速选择)算法。这个名字和 quick sort(快速排序)看起来很像,算法的思想也和快速排序类似,都是分治法的思想。
算法的复杂度分析:
- 空间复杂度 O(1),不需要额外空间。
- 时间复杂度的分析方法和快速排序类似。由于快速选择只需要递归一边的数组,时间复杂度小于快速排序,期望时间复杂度为 O(n),最坏情况下的时间复杂度为 O(n2)。
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k==0){
return new int[0];
}else if(arr.length<=k){
return arr;
}
partitionArray(arr,0,arr.length-1,k);
int[] res=new int[k];
for(int i=0;i<k;i++){
res[i]=arr[i];
}
return res;
}
void partitionArray(int[] arr,int lo,int hi,int k){
int m=partition(arr,lo,hi);
if(k==m){
return;
}else if(k<m){
partitionArray(arr,lo,m-1,k);
}else if(k>m){
partitionArray(arr,m+1,hi,k);
}
}
int partition(int[] arr,int lo,int hi){
int i=lo,j=hi;
int tmp=arr[lo];
while(i<j){
while(i<j&&tmp<=arr[j]) j--;
arr[i]=arr[j];
while(i<j&&tmp>=arr[i]) i++;
arr[j]=arr[i];
}
arr[i]=tmp;
return i;
}
}
面试题41. 数据流中的中位数
题目
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
输入:
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]
主要思想是维护一个动态的有序序列,获取中位数。
所以两个关键:怎样快速维护有序序列;怎样快速得到中位数是谁。
很巧妙的思路,利用两个优先队列分别表示大顶堆和小顶堆。
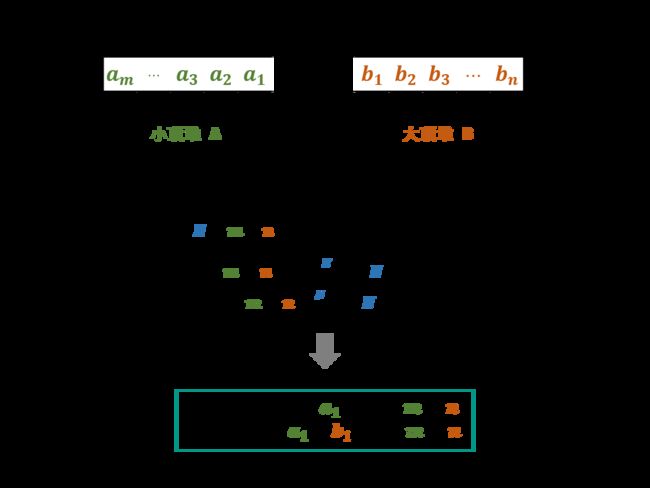
这里分别使用三种语言,回忆一下各自的优先队列使用。
1)C++版:
优先队列使用参考
默认是从大到小排序
class MedianFinder {
public:
priority_queue<int,vector<int>,greater<int>> a;//从小到大,存储大的一半
priority_queue<int,vector<int>> b;//从大到小,存储小的一半
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
int m=a.size(),n=b.size();
if(m!=n){
a.push(num);
b.push(a.top());a.pop();
}
else{
b.push(num);
a.push(b.top());b.pop();
}
}
double findMedian() {
return a.size()==b.size()?(a.top()+b.top())/2.0 : a.top();
}
};
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder* obj = new MedianFinder();
* obj->addNum(num);
* double param_2 = obj->findMedian();
*/
2)java版
参考
默认从小到大排列
class MedianFinder {
Queue<Integer> a,b;
/** initialize your data structure here. */
public MedianFinder() {
a=new PriorityQueue<Integer>();//小顶堆
b=new PriorityQueue<Integer>((x, y) -> (y - x));//大顶堆
}
public void addNum(int num) {
if(a.size()!=b.size()){
a.add(num);
b.add(a.poll());
}else{
b.add(num);
a.add(b.poll());
}
}
public double findMedian() {
return a.size()==b.size()? (a.peek()+b.peek())/2.0 : a.peek();
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
3)python:
python堆队列
小顶堆,从小到大
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] # 小顶堆,保存较大的一半
self.B = [] # 大顶堆,保存较小的一半
def addNum(self, num: int) -> None:
if len(self.A) != len(self.B):
heappush(self.B, -heappushpop(self.A, num))
else:
heappush(self.A, -heappushpop(self.B, -num))
def findMedian(self) -> float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
面试题43. 1~n整数中1出现的次数
题目
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
输入:n = 12
输出:5
解释:1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次
这道题自己开始真的毫无思路啊,找到两种方法可以看懂的题解。
- 递归
参考题解
class Solution {
public int countDigitOne(int n) {
return f(n);
}
private int f(int n ) {
if (n <= 0)
return 0;
String s = String.valueOf(n);
int high = s.charAt(0) - '0';
int pow = (int) Math.pow(10, s.length()-1);
int last = n - high*pow;
if (high == 1) {
return f(pow-1) + last + 1 + f(last);
} else {
return pow + high*f(pow-1) + f(last);
}
}
}
- 找规律
参考题解
我们假设高位为high,当前位为cur,低位为low,i代表着需要统计的位置数(1对应个位,10对应十位,100对应百位),则对每一位的个数count有:
cur=0,count=high x i
cur=1,count=high x i+low+1;
cur>1,count=high x i+i
最终累加所有位置上的个数即最终答案。
class Solution {
public:
int countDigitOne(int n) {
int count = 0;
long i = 1;//指向遍历的位数,如i=1即个位,i=10即十位,...,因为n可以有31位,所以10^31用long存储
while(n/i!=0){
//n/i控制遍历的次数,将所有的位数都遍历完毕
long high = n/(10*i);//将当前位之前的所有高位都存在high中
long cur = (n/i)%10;//将当前位记录在cur中,即我们每次都需要统计当前位上1出现的次数
long low = n-(n/i)*i;
if(cur == 0){
count += high * i;
} else if(cur == 1){
count += high * i + low + 1;
} else {
count += high * i + i;
}
i = i * 10;//准备遍历下一位
}
return count;
}
};
面试题44. 数字序列中某一位的数字
题目
数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从下标0开始计数)是5,第13位是1,第19位是4,等等。
请写一个函数,求任意第n位对应的数字。
1位:0-9 9个数字
2位:10-99 90个
3位:100-999 900个
…
只要找到该数字在第几位的数字中,排列在第几个,就能只知道具体数字是几,得出答案。
class Solution {
typedef long long ll;
public:
int findNthDigit(int n) {
int k=1;
ll base=1;
ll sum=9;
while(sum<n){
n-=sum;
k++;
base=base*10;
sum=k*base*9;
}
ll num=base+(n-1)/k;
return to_string(num)[(n-1)%k]-'0';
}
};
面试题49. 丑数
题目
我们把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
1 是丑数。
n 不超过1690。
思路真的非常巧妙。
关键的思路是:
丑数的递推性质: 丑数只包含因子 2, 3, 5,因此有 “丑数 == 某较小丑数× 某因子” (例如:10=5×2)
主要是2,3,5乘积的各种混合组合,然后要让越小的越靠前,这就是三组a,b,c递推的缘由。
class Solution {
public:
int nthUglyNumber(int n) {
int a=0,b=0,c=0;
int dp[1691];
dp[0]=1;
for(int i=1;i<n;i++){
int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
dp[i] = min(min(n2, n3), n5);
if(dp[i] == n2) a++;
if(dp[i] == n3) b++;
if(dp[i] == n5) c++;
}
return dp[n-1];
}
};
面试题57. 和为s的两个数字
题目
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
双指针确定区间。
class Solution {
public int[] twoSum(int[] nums, int target) {
int l=0,r=nums.length-1;
int res[]=new int[2];
while(l<=r){
if(nums[l]+nums[r]>target){
r--;
}else if(nums[l]+nums[r]<target){
l++;
}else{
res[0]=nums[l];
res[1]=nums[r];
break;
}
}
return res;
}
}
面试题57 - II. 和为s的连续正数序列
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
滑动窗口(双指针)
至少包含两个数,可以得到正整数序列的右区间范围是(r+1)/2
# 滑动窗口
class Solution:
def findContinuousSequence(self, target: int) -> List[List[int]]:
l=1;r=2
res=[]
sum=l+r
while l<r and r<=(target/2+1):
if sum<target:
r+=1
sum+=r
while sum>target:
sum-=l
l+=1
if sum==target:
temp=[]
for i in range(l,r+1):
temp.append(i)
res.append(temp)
r+=1
sum+=r
return res
面试题58 - I. 翻转单词顺序
题目
很简单的题目,也能从优秀题解中学到很多。
语法知识:python的split() 方法可以将单词间的 “多个空格看作一个空格” 。
面试题58 - II. 左旋转字符串
题目
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串"abcdefg"和数字2,该函数将返回左旋转两位得到的结果"cdefgab"。
取余操作很妙。
class Solution {
public:
string reverseLeftWords(string s, int n) {
string res;
int len=s.length();
for(int i=n;i<len+n;i++){
res+=s[i%len];
}
return res;
}
};
面试题60. n个骰子的点数
题目
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
梳理整个过程:
- 每个点数之和出现的概率:该点数和出现的次数 / 所有可能点数和出现次数
- 所有点数和出现次数:6n
问题转化为:投掷完 n 枚骰子后每个点数出现的次数。
求解方法:动态规划
dp[i][j]:投掷 i 枚骰子后,点数和为 j 出现的次数。
那么最后dp[n][j]就是要求的概率数组。
递推公式:
dp[n][j]=sum(dp[n-1][j-i]) (1<=i
初始化:
dp[1][j]=1 投掷一枚骰子,不论是几,出现次数都是1.
class Solution {
public:
vector<double> twoSum(int n) {
int dp[15][70];
memset(dp,0,sizeof(dp));
//初始化
for(int i=1;i<=6;i++){
dp[1][i]=1;
}
//递推
for(int i=2;i<=n;i++){
for(int j=i;j<=6*i;j++){
for(int k=1;k<=6;k++){
if(k>=j) break;
dp[i][j]+=dp[i-1][j-k];
}
}
}
//得到结果
int p=pow(6,n);
vector<double> res;
for(int i=n;i<=6*n;i++){
res.push_back(dp[n][i]*1.0/p);
}
return res;
}
};
面试题61. 扑克牌中的顺子
题目
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
输入: [0,0,1,2,5]
输出: True
自己想到的就是单纯的遍历模拟,虽然和下面另一种判断的时间一样,但是代码会很复杂。
class Solution {
public boolean isStraight(int[] nums) {
Arrays.sort(nums);
int k=0;
for(int i=0;i<nums.length;i++){
if(nums[i]==0){
k++;
continue;
}
if(i<nums.length-1){
if(nums[i+1]-nums[i]>1){
k-=(nums[i+1]-nums[i]-1);
if(k<0){
return false;
}
}
else if(nums[i+1]-nums[i]==0){
return false;
}
}
}
return true;
}
}
题解的大致思想虽然是一致的,但是判断非常巧妙,不需要判断大小王到底是去替代几,或者在哪里替代,直接使用了一个序列最大值max-序列最小值min<5来做判断是否是连续数组,太巧妙了。
分别使用了set和排序两种方式判断序列中重复问题。
- set
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
max = Math.max(max, num); // 最大牌
min = Math.min(min, num); // 最小牌
if(repeat.contains(num)) return false; // 若有重复,提前返回 false
repeat.add(num); // 添加此牌至 Set
}
return max - min < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}
- 排序
class Solution {
public boolean isStraight(int[] nums) {
int joker = 0;
Arrays.sort(nums); // 数组排序
for(int i = 0; i < 4; i++) {
if(nums[i] == 0) joker++; // 统计大小王数量
else if(nums[i] == nums[i + 1]) return false; // 若有重复,提前返回 false
}
return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}
面试题62. 圆圈中最后剩下的数字
题目
0,1,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
输入: n = 5, m = 3
输出: 3
0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
约瑟夫环问题。
很好的题解
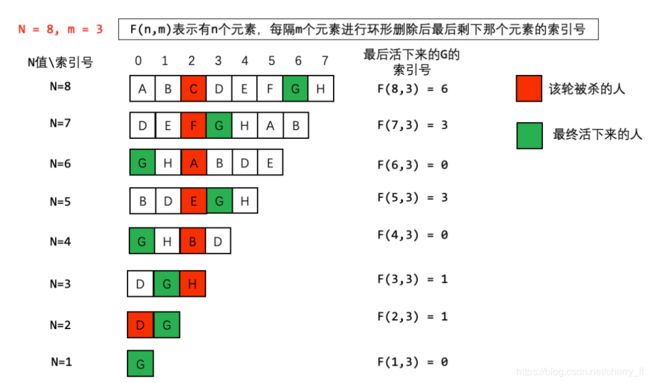
反推:

递推公式:f(n,m)=[f(n−1,m)+m]%n
class Solution {
public:
int lastRemaining(int n, int m) {
int last=0;
for(int i=2;i<=n;i++){
last=(last+m)%i;
}
return last;
}
};
面试题63. 股票的最大利润
题目
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int minPrice=0x3f3f3f3f,maxProfit=0;
int n=prices.size();
for(int i=0;i<n;i++){
minPrice=min(minPrice,prices[i]);
maxProfit=max(maxProfit,prices[i]-minPrice);
}
return maxProfit;
}
};
面试题64. 求1+2+…+n
求 1+2+…+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
//采用逻辑与的短路特性
class Solution {
public int sumNums(int n) {
int sum=n;
boolean ans=(n>0) && ((sum+=sumNums(n-1))>0);
return sum;
}
}
面试题65. 不用加减乘除做加法
题目
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
class Solution {
public int add(int a, int b) {
int sum,carry;
do{
sum=a^b;
carry=(a&b)<<1;
a=sum;
b=carry;
}while(b!=0);
return sum;
}
}