GZIP压缩原理分析（32）——第五章 Deflate算法详解（五23） 动态哈夫曼编码分析（12）构建哈夫曼树（04）

*构建literal/length树

博客http://www.cnblogs.com/esingchan/p/3958962.html中这样说道：“ZIP之所以是通用压缩，它实际上是针对字节作为基本字符来编码的，所以一个literal至多有256种可能”。Literal其实就是一个字节所能表示的所有字符，包括可见与不可见的，从十进制0到255，共256种。Length表示匹配串长度，匹配串最小长度为3，这点我们已经在LZ77章节中多次提到；匹配串长度不是无限的，最大长度为258，所以length共有256种，范围对应闭区间[3, 258]。如果实际匹配长度超过258，后面的匹配部分就再用一个长度距离对儿表示。

 

为什么literal和length的取值个数都是256，都可以用一个字节表示，这是巧合吗？虽然那个隐含假设告诉我们相同的内容总是扎堆儿出现，但为什么length的最大值偏偏是258？一路分析过来，我们已经发现，压缩中任何一个数据的设计都不是巧合，都是刻意为之，都是有实际意义的！这种设计可以让literal和length共用同一棵哈夫曼树，一次编码同时得到literal和length的码字。

 

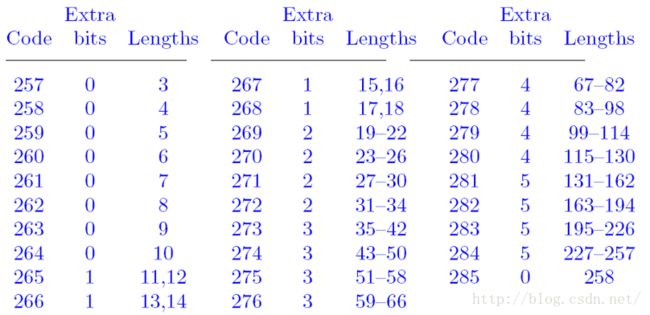
Literal的范围是闭区间[0, 255]，length的范围是闭区间[3, 258]。压缩将这两个区间编到同一张表中，从而将其整合到一起。闭区间[0, 255]仍然表示literal，关系是一对一的，一个数对应一个literal；256代表本压缩块的结束（前面我们讲过压缩是分块进行的）；length共有256种值，和distance一样，为了优化，将这256个值分到不同的区间，共有29个区间，区间码范围为闭区间[257, 285]。如下表所示（length区间码表），

该表原理以及使用方法与distance区间码表是完全相同的。

 

闭区间[0, 285]将literal和length全部整合在一起，哈夫曼编码就是针对这个闭区间进行的。[0, 256]是一对一的关系，参与哈夫曼编码过程；[257, 285]是length的区间码，这29个值参与哈夫曼编码过程而不是256个length值参与哈夫曼编码过程（与distance的使用方法是相同的）。压缩结果也需要记录闭区间[0, 285]这286个数的码字长度，记录方法与distance相同，使用一个数列，每个数在数列中的顺序（从0开始）代表该数在闭区间[0, 285]中对应的值，而这个数本身代表该值的码字长度。例如数列

“0、0、0、0、0、0、0、0、1、0、0、2、0、0、0、0、4、0、0……”，

该数列共有286个数，第零个0，表示闭区间[0, 258]中的零的码字长度是0；第一个0，表示闭区间[0, 258]中的一的码字长度是0；第二个0，表示闭区间[0, 258]中的二的码字长度是0……第八个1，表示闭区间[0, 258]中的八的码字长度是1……第十一个2，表示闭区间[0, 258]中的十一的码字长度是2……第十六个4，表示闭区间[0, 258]中的十六的码字长度是4……

 

现在我们为字符串“As mentioned above,there a(3,01)many kinds of wirelesssystem(3,0110)(4,100111) than cellular.”中的literal和length编码。统计该字符串中每个literal的出现频率，并将[0, 258]中未在该字符出现的literal的频率记为0；将闭区间[0, 258]中的256的出现频率记为1，作为压缩块结束标记；该字符串中的length为3、3、4，对应区间码分别为257、257、258，其中，区间码257出现两次，区间码258出现一次，其余length区间码出现频率全部为0。

 

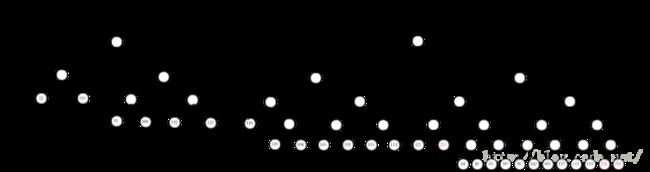
根据以上信息，构造哈夫曼树。因为原始哈夫曼树各节点深度与范式哈夫曼树相同，所以简单起见，我们这里专门构造一棵范式哈夫曼树来说明。如下图所示，

根据这棵树我们可以得到literal和length的码字，每个叶子节点都用闭区间[0, 285]中的值表示。Length区间码为257和258的码字分别为二进制“11001”和“111111”；块结束标记256的码字为二进制“111110”；其他各叶子节点都是literal的码字。Length值的码字也需要用“区间码码字+扩展位编码”合成，合成方法与distance值的码字合成方法相同，这里不再赘述。

 

码表如下，

Literal码表
Literal值	ASCII字符	码字直接计算结果	实际码字（作为压缩结果，从右往左看）
32	空格	000	000
101	e	001	100
97	a	0100	0010
108	l	0101	1010
110	n	0110	0110
115	s	0111	1110
116	t	1000	0001
100	d	10010	01001
104	h	10011	11001
105	i	10100	00101
109	m	10101	10101
111	o	10110	01101
114	r	10111	11101
121	y	11000	00011
44	,	110100	001011
46	.	110101	101011
65	A	110110	011011
98	b	110111	111011
99	c	111000	000111
102	f	111001	100111
107	k	111010	010111
117	u	111011	110111
118	v	111100	001111
119	w	111101	101111
256	无	111110	011111

从这张码表可以看出很多东西，比如前缀码、范式哈夫曼编码的各个性质、每层的码字长度、出现频率越高的字符码字长度越短等。

Length码表
Length值	区间码码字	扩展位编码	Length码字（作为压缩结果，从右往左看）
3	11001	无扩展位	10011
4	111111	无扩展位	111111

 码表已经得到，现在就可以对着这两张码表将字符串“As mentioned above,there a(3,01)many kinds of wirelesssystem(3,0110)(4,100111) than cellular.”彻底从字节流编程比特流。开始转换：

“A(011011)s(1110) (000)m(10101)e(100)n(0110)t(0001)i(00101)o(01101)n(0110)e(100)d(01001) (000)a(0010)b(111011)o(01101)v(001111)e(100),(001011)t(0001)h(11001)e(100)r(11101)e(100)(000)a(0010) (3(10011),01)m(10101)a(0010)n(0110)y(00011)(000)k(010111)i(00101)n(0110)d(01001)s(1110)(000)o(01101)f(100111)(000)w(101111)i(00101)r(11101)e(100)l(1010)e(100)s(1110)s(1110)(000)s(1110)y(00011)s(1110)t(0001)e(100)m(10101) (3(10011),0110)(4(111111),100111) (000)t(0001)h(11001)a(0010)n(0110)(000)c(000111)e(100)l(1010)l(1010)u(110111)l(1010)a(0010)r(11101).(101011)”。

 

每个字符都已经找到了自己的码字，但此时并不能直接用码字把原码替换掉！虽然现在已经是比特流，但在内存或存储介质中，压缩结果必须按照字节的方式存储，也就是说，这条比特流必须放到一个个的字节中去！现在，每个码字本身已经符合内存中的实际存储方式（即原始计算结果的逆序），但是码字与码字之间还没有符合实际的存储方式。将码字填入字节时，要从该字节的低位开始填起，比如，先将A填入一个字节，再将s填入该字节，那么A的码字占据该字节的低位而s的码字占据该字节的高位，以此类推，只要保证从每个字节的低位开始填起就没有问题。如果一个字节剩余的比特位不足以放下整个码字，则该码字从右往左能放几比特就放几比特，这个码字剩下那几个比特就放到另外一个字节中。一定要看懂这个地方，会直接影响到后面的源码分析的。

 

将A的码字的低两位放到另外一个字节，原因我们后续分析。末尾要带上256的码字，如果不够一个字节，就用0补齐剩下的比特。不同的码字用不同的颜色进行区分，填充开始：

11

11100110   10101000    10110100    00101000    11001101   10011000    00100000    01111011

01111011   10111000    01000100    01100110    00100111   01100100    01010110    11000101

00000110   10101110    01100010    11001001    11010001   01001110    10111100    10100101

01010011   11101001    00001110    00011111    00011110   10101100    11010011    11111110

00010011   10010001    11000101    01110000    01010000   11110101    01010110    11101001

11101011   00000111

每看一个字节的时候，要从右往左看，就可以看出码字，一个码字可能会跨越两个字节。对应的十六进制结果是（不看A让出去的那两位）：

E6    A8    B4    28    CD    98    20    7B

7B    B8    44    66    27     64    56    C5

06    AE    62    C9    D1    4E    BC    A5

53    E9    0E    1F     1E    AC    D3    FE

13    91    C5   70     50    F5     56    E9

EB    07

最后用256的码字表示该压缩块的结束，但是还剩4bits才够一个字节，所以剩下的4bits就全部用0补齐（这一点很重要，源码分析要用）。

 

这就是实际的压缩结果，这个过程是我们完全用人工计算出来的，现在看看压缩工具的压缩结果，如下图所示，

  和我们人工压缩结果是完全相同的。

 

对着上面的比特流，有没有产生这样一个问题：这个比特流由两张码表构成（literal码表和length码表同属literal/length码表，为了说明方便才分开。另一个码表是distance码表），怎么知道一个码字该用哪张码表去解码？其实很简单，开始解码的时候就用literal码表解码，当发现一个码字无法解码时，说明这个码字肯定是length的码字，用length码表解码；length后面跟着的肯定是distance码字，所以解完length，后面的那个码字就用distance码表解码；解完distance码字，再接着用literal码表解后续的码字，重复这个过程即可。

 

之所以能这样解码，与压缩时每个码字放到比特流中的顺序是分不开的。前面讲LZ77的时候说过，待压缩数据的首个字符不参与匹配过程，也就是说，长度距离对儿肯定不会在压缩块的开始位置出现（用脚趾头都能想明白），所以解码整个压缩块的首个码字就用literal码表；每个长度距离对儿，distance的码字都在length码字的后面，从上面的比特流就可以看出，压缩时先把length的码字扔到比特流里，再把distance的码字扔到比特流里，distance码字紧跟在length码字后面。

 

再次提醒，literal码表和length码表同属literal/length码表，literal/length码表是“一”张表，与distance码表并列。

 

现在LZ77之后的结果已经全部转换成了比特流，但是压缩远没有结束，别忘了，还要记录生成literal/length树的信息。闭区间[0, 285]中各值的码字长度数列如下，

0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、3、0、0、0、0、0、0、0、0、0、0、0、6、0、6、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、6、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、4、6、6、5、3、6、0、5、5、0、6、4、5、4、5、0、0、5、4、4、6、6、6、0、5、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、6、5、6、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0

 

Distance各区间码的码字长度数列如下，

0、0、0、2、0、0、0、0、1、0、2、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0

 

原始字符串被压缩之后的比特流如下，

11

11100110    10101000   10110100    00101000    11001101   10011000    00100000    01111011

01111011    10111000   01000100    01100110    00100111   01100100    01010110    11000101

00000110    10101110   01100010    11001001    11010001   01001110    10111100    10100101

01010011    11101001   00001110    00011111    00011110   10101100    11010011    11111110

00010011    10010001   11000101    01110000    01010000   11110101    01010110    11101001

11101011    00000111

 

这个时候的压缩结果，已经基本具有了雏形，该有的基本都有了：码字长度信息+实际压缩数据。但是压缩并没有结束，这并不是最优的压缩结果，还有继续压缩的空间。