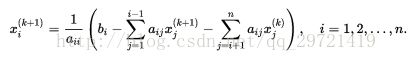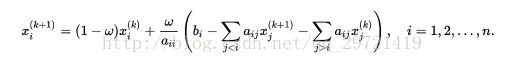数值计算——线性方程组的迭代法
数值计算——线性方程组的迭代法
与上一篇中的直接法相比，迭代法是从解的一个初始估计值除法，逐步对他进行改进，知道到达所需的精度，理论上来说，经过无限次的迭代之后就可以得到真解，但实际上只需要达到所需要的精度即可。下面是几种迭代法：
- 雅克比方法
- 高斯-赛德尔方法
- 逐次超松弛法
使用迭代法的关键在于
：
-
- 确定迭代变量：在可以用迭代算法解决的问题中，至少存在一个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。
- 确定迭代关系式：所谓迭代关系式，指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键，通常可以顺推或倒推的方法来完成。
- 对迭代过程进行控制：在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值，可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况，需要进一步分析出用来结束迭代过程的条件。
一、雅克比方法
首先将方程组
中的系数矩阵
A
分解成三部分，即:
A = L+D+U
，如图所示，
其中D为对角阵，L为下三角矩阵，U为上三角矩阵。
之后确定迭代格式:X^(k+1) = D^(-1)(b-(L+U)x^(k)) ,这里^表示的是上标，括号内数字即迭代次数(k = 0,1，......)
再选取初始迭代向量X^(0)，开始逐次迭代。
雅克比迭代法的优点明显，计算公式简单，且计算过程中原始矩阵A始终不变，比较容易并行计算。然而这种迭代方式收敛速度较慢，而且占据的存储空间较大，所以工程中一般不直接用雅克比迭代法，而用其改进方法。
使用雅克比方法并不总是收敛的，一般当矩阵式行对角占优的时候是收敛的。
程序实现：
/**
* Jacobi迭代法
* @param a
* @param b
* @return
*/
public static double[] Jacobi(double[][] a, double[] b) {
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
sum += a[i][j] * x[j];
}
}
y[i] = (b[i] - sum) / a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}二、高斯-赛德尔方法
雅克比方法收敛速度缓慢的原因之一是它在迭代过程中并没有使用最新的信息：新的分量值只有在整个扫描过程全部完成之后才能被利用。Gauss-Seidel方法弥补了这一缺陷，一旦某个分量的新值计算出来马上将他利用。
将矩阵A分成两部分：A=(L+D)+U
选取迭代格式：x^(k+1)=(D+L)^(-1)(b-Ux^(k))
在选取初始向量，然后逐次迭代。
高斯-赛德尔方法还有一个优点就是不需要对向量x做重复存储。
程序实现：
/**
* 高斯-赛德尔方法
* @param a
* @param b
* @return
*/
public static double[] GaussSeidel(double[][] a,double[] b){
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//跟Jacobi的不同之处
if (i < j) {
sum += a[i][j] * y[j];
}else if(i>j){
sum += a[i][j] * x[j];
}
}
y[i] = (b[i] - sum) / a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}三、逐次超松弛方法（SOR）
SOR技术可以加快Gauss-Seidel方法的收敛速度，就是从x^(k)出发，首先使用Gauss-Seidel方法计算下一步的迭代值x^(k+1)，然后取下一次迭代值为：
那么迭代式为：
当步长<1时称为低松弛即向后搜索，=1时为Gauss-Seidel，>1时为超松弛，即向前搜索
程序实现：
/**
* 逐次超松弛方法SOR
* @param a
* @param b
* @return
*/
public static double[] SOR(double[][] a,double[] b,double m){
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//跟Jacobi的不同之处
if (i < j) {
sum += a[i][j] * y[j];
}else if(i>j){
sum += a[i][j] * x[j];
}
}
y[i] = (1-m)*x[i]+(m*(b[i] - sum))/ a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}package com.kexin.lab3;
/**
* 用迭代法求解线性方程组： Jacobi、Gauss-Seidel、SOR
*
* @author KeXin
*
*/
public class DieDai {
/**
* Jacobi迭代法
* @param a
* @param b
* @return
*/
public static double[] Jacobi(double[][] a, double[] b) {
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
sum += a[i][j] * x[j];
}
}
y[i] = (b[i] - sum) / a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}
/**
* 高斯-赛德尔方法
* @param a
* @param b
* @return
*/
public static double[] GaussSeidel(double[][] a,double[] b){
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//跟Jacobi的不同之处
if (i < j) {
sum += a[i][j] * y[j];
}else if(i>j){
sum += a[i][j] * x[j];
}
}
y[i] = (b[i] - sum) / a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}
/**
* 逐次超松弛方法SOR
* @param a
* @param b
* @return
*/
public static double[] SOR(double[][] a,double[] b,double m){
int n = a.length;
double sum = 0;
double e = 0.001;
double z;
int i;
double[] x = new double[n];
double[] y = new double[n];
while (true) {
//按迭代式迭代
for (i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//跟Jacobi的不同之处
if (i < j) {
sum += a[i][j] * y[j];
}else if(i>j){
sum += a[i][j] * x[j];
}
}
y[i] = (1-m)*x[i]+(m*(b[i] - sum))/ a[i][i];
sum = 0;
}
//达到精度后终止
i = 0;
while (i < n) {
z = Math.abs(x[i] - y[i]);
if (z > e)
break;
i++;
}
if (i != n) {
for (i = 0; i < n; i++)
x[i] = y[i];
}else if (i == n)
break;
}
return y;
}
/**
* 打印数组
* @param result
*/
public static void PrintArray(String str,double[] result){
int n = result.length;
System.out.print(str + "\n[");
for(int i =0;i