二刷剑指Offer：剑指Offer+LeetCode（全53题）

剑指Offer刷题

67. 剪绳子（贪心算法）

1、题目：

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1]...k[m-1]。请问 k[0]*k[1]*...*k[m-1]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

2、思路：

https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/mian-shi-ti-14-i-jian-sheng-zi-tan-xin-si-xiang-by/

时间复杂度：O(1)

空间复杂度：O(1)

public class Solution {
    public int cutRope(int target) {
        /**
         * 根据数学推导，如果把绳子切成长度为3的多段，乘积最大
         *
         * 假如把绳子切成长度为3的多段，那么留下来的最后一段的绳子可能为0、1、2三种情况
         * 假如余下的绳子长度为2，应该保留不再拆分为2=1+1,因为1*1 < 2
         * 假如余下的绳子长度为1，那么应该把一个3+1替换成2+2，因为3*1 < 2*2
         */

        /**
         * 算法流程：
         * 当 n≤3 时，即n=2或3时，按照规则应不切分，但由于题目要求必须剪成 m>1 段
         *            因此必须剪出一段长度为 1 的绳子，2=1+1，即返回 n−1。
         *
         * 当 n>3 时，求n/3的整数部分 a 和余数部分b(n=3a+b)
         *      1、如果b=0，  返回3^a
         *      2、如果b=1，  返回4*3^(a-1)  （3+1->2+2）
         *      3、如果b=2，  返回2*3^a
         */

        if(target<=3){
            return target-1;
        }

        //整数部分
        int a = target/3;
        //余数部分
        int b = target%3;

        if(b==0){
            return (int) Math.pow(3,a);
        }else if(b==1){
            return (int) (Math.pow(3,a-1)*4);
        }else {
            return (int) (Math.pow(3,a)*2);
        }
    }
}

66. 机器人的运动范围（dfs）

1、题目：

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

2、思路：

时间复杂度：O(m*n)：二维数组的行和列

空间复杂度：O(m*n)：创建一个二维数组

public class Solution {
    public int movingCount(int threshold, int rows, int cols) {
        for(int x=0;x<rows;x++){
            for(int y=0;y<cols;y++){
                return dfs(x,y,rows,cols,threshold,new boolean[rows][cols]);
            }
        }
        return 0;
    }

    /**
     * @param x 机器人位置的横坐标
     * @param y 机器然位置的纵坐标
     * @param rows 二维数组的行
     * @param cols 二维数组的列
     * @param threshold k
     * @param visited 标记该位置是否走过
     *
     * @return 机器人走的格子
     */
   private int dfs(int x, int y, int rows, int cols, int threshold, boolean[][] visited){
        //递归结束的条件

        //1. 如果机器人走的路径越界了
        if(x<0 || y<0 || x>rows-1 || y>cols-1) return 0;

        //2. 行坐标和列坐标的数位之和大于k的格子
        if(x/10+x%10+y/10+y%10 > threshold) return 0;

        //3. 走过的格子不能重复走
        if(visited[x][y]) return 0;

        //将走过的格子标记为true
        visited[x][y] = true;

        //每移动一个格子就加1,
        return  dfs(x-1,y,rows,cols,threshold,visited)      //向左移动
               +dfs(x+1,y,rows,cols,threshold,visited)      //向右移动
               +dfs(x,y-1,rows,cols,threshold,visited)      //向下移动
               +dfs(x,y+1,rows,cols,threshold,visited)+1;   //向上移动
    }
}

65. 矩阵中的路径（回溯算法）

1、题目：

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

2、思路：

时间复杂度：O(m*n)：二维数组的行和列

空间复杂度：O(m*n)：创建一个二维数组

public class Solution {
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
        boolean[][] visited = new boolean[rows][cols];
        for(int i=0;i<=rows-1;i++){
            for(int j=0;j<=cols-1;j++){
               if(dfs(matrix,rows,cols,i,j,str,0,visited)){
                   return true;
               }
            }
        }
        return false;
    }

    private boolean dfs(char[] matrix, int rows, int cols, int x, int y, char[] str, int k, boolean[][] visited) {

        //如果超出矩阵范围，返回false
        if(x<0||x>rows-1||y<0||y>cols-1) return false;

        //如果已经走过的路径，就不能再走，返回false
        if(visited[x][y]) return false;

        //如果走到的位置处的字符和字符串中的字符不相等，返回false
        if(str[k] != matrix[x*cols+y]) return false;

        //如果前面都满足条件，并且字符串遍历到最后一个，返回true
        if(k==str.length-1) return true;

        //在递归之前开始选择，用visited标记该路径已经选择
        visited[x][y] = true;
        boolean flag = dfs(matrix,rows,cols,x-1,y,str,k+1,visited)
                || dfs(matrix,rows,cols,x+1,y,str,k+1,visited)
                || dfs(matrix,rows,cols,x,y+1,str,k+1,visited)
                || dfs(matrix,rows,cols,x,y-1,str,k+1,visited);

        //在递归结束之后撤销选择，用visited标记该路径撤销了选择
        if(!flag){
            visited[x][y] = false;
        }
        return flag;
    }
}

64. 滑动窗口的最大值（双端队列）

1、题目：给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

2、思路：

https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/solution/java-dan-diao-shuang-xiang-lian-biao-hua-tu-xiang-/

我们维护一个单调的双向队列，窗口在每次滑动的时候，我就从队列头部取当前窗口中的最大值，每次窗口新进来一个元素的时候，我就将它与队列中的元素进行大小比较：

如果刚刚进来的元素比队列的尾部元素大，先将队列尾部的元素弹出，然后把刚刚进来的元素添到队列的尾部；
如果刚刚进来的元素比队列的尾部元素小，那么把刚刚进来的元素直接添到队列的尾部即可。

剑指Offer作答：

import java.util.ArrayList;
import java.util.LinkedList;

public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size) {
        if(num==null || size<1 || num.length<size){
            return new ArrayList<>();
        }
        
        LinkedList<Integer> queue = new LinkedList<>();
        ArrayList<Integer> res = new ArrayList<>();
        int n = num.length;
        for(int i=0;i<=n-1;i++){
            //如果窗口尾部的元素比当前元素小，或者相等，就让窗口尾部的元素弹出
            while(!queue.isEmpty() && num[queue.peekLast()] <= num[i]){
                queue.pollLast();
            }
            //否则当前运算正常入队
            queue.addLast(i);
            
            //如果滑动窗口已经略过了队列中头部的元素，则将头部元素弹出
            if(queue.peekFirst()==(i-size)){
                queue.pollFirst();
            }
            
            //如果窗口形成了，就开始取出最大值
            //一开始进入队列，要看看窗口有没有形成，只有形成了大小为 k 的窗口，我才能收集窗口内的最大值
            //一旦窗口形成，之后每进入一个元素就可以取出最大值了
            if(i-size+1>=0){
                res.add(num[queue.peekFirst()]);
            }
        }
        return res;
    }
}

63. 数据流中的中位数

1、题目：

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，[2,3,4] 的中位数是 3；[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

2、思路：

一个基于优先级堆的无界优先级队列。优先级队列的元素按照其自然顺序进行排序，或者根据构造队列时提供的 Comparator 进行排序，具体取决于所使用的构造方法。此队列的头 是按指定排序方式确定的最小元素。

PriorityQueue默认实现的是小顶堆，堆顶为最小的元素。也可以自定义排序方式实现大顶堆，堆顶为最大的元素

https://leetcode-cn.com/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof/solution/mian-shi-ti-41-shu-ju-liu-zhong-de-zhong-wei-shu-y/

/**
 *   每次插入小顶堆的是当前大顶堆中最大的数
 *   每次插入大顶堆的是当前小顶堆中最小的数
 *   这样保证小顶堆中的数永远大于等于大顶堆中的数
 *   中位数就可以方便地从两者的根结点中获取了
 *
 * 为了保持让大顶堆存放较小的元素，小顶堆存放较大的元素
 * 当插入元素num时，num可能为较小的元素，因此先将num插入到大顶堆中，（插入后会自动排序）
 * 然后从大顶堆的堆顶弹出最大的元素放入到小顶堆中
 */
public class Solution {
    //创建一个小顶堆存放较大的元素
    Queue<Integer> min = new PriorityQueue<>();

    //创建一个大顶堆存放较小的元素
    Queue<Integer> max = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return  o2-o1;
        }
    });
    
    public void Insert(Integer num) {
        //如果个数元素分数不等，说明大顶堆多了一个元素
        if(min.size()!=max.size()){
            max.add(num);
            min.add(max.poll());
        }else{
            min.add(num);
            max.add(min.poll());
        }
    }

    public Double GetMedian() {
        if(max.size() != min.size()){
            return (double) max.peek();
        }
        return (double)(min.peek()+max.peek())/2;
    }
}

62. 二叉搜索树的第k大节点（Leedcode）

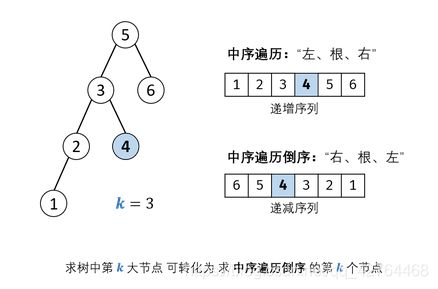
题目：给定一棵二叉搜索树，请找出其中第k大的节点。

思路：二叉搜索树的中序遍历为 递增序列 。

https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/solution/mian-shi-ti-54-er-cha-sou-suo-shu-de-di-k-da-jie-d/

中序遍历的遍历顺序为：左子节点、根节点、右子节点，遍历的结果是元素时排好序的且是递增的。

如果遍历的时候右、根、左，那么遍历的结果中顺序就是递减的。

class Solution {
    int res;
    int k;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return res;
    }

    private void dfs(TreeNode root) {
        if(root==null) return;
        //遍历右子树
        dfs(root.right);
        
        // 根节点
        k = k-1;
        //如果k=0,说明找到了，直接返回
        if(k==0) {
            res = root.val;
            return;
        }
        
        //遍历左子树
        dfs(root.left);
    }
}

62. 二叉搜索树的第k小节点（中序遍历）

题目：给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。

代码：二叉树的中序遍历是有序的，并且是单调递增的。

public class Solution {
    TreeNode res;
    int k;
    TreeNode KthNode(TreeNode pRoot, int k) {
        this.k = k;
        dfs(pRoot);
        return res;
    }

    private void dfs(TreeNode pRoot) {
        //递归终止的条件
        if(pRoot==null) return;

        //遍历左子树
        dfs(pRoot.left);

        if(k==0) return;
        //当前节点
        if(--k==0){
            res = pRoot;
        }
        
        //遍历右子树
        dfs(pRoot.right);
    }
}

61. 序列化二叉树（Leetcode）

题目：请实现两个函数，分别用来序列化和反序列化二叉树。

思路：https://leetcode-cn.com/problems/xu-lie-hua-er-cha-shu-lcof/solution/mian-shi-ti-37-xu-lie-hua-er-cha-shu-ceng-xu-bian-/

时间复杂度：O(n)；空间复杂度：O(n)

/**
        1

    2       3

        4       5

 [1,2,3,null,null,4,5,null,null,null,null]
 */
public class Codec {
    public String serialize(TreeNode root) {
        
        //利用层序遍历将二叉树序列化为字符串
        if(root==null) return "[]";
        StringBuilder sb = new StringBuilder();
        sb.append("[");
        
        //创建一个队列
        Queue<TreeNode> queue = new LinkedList<>();
        //将根结点入队
        queue.add(root);
        
        while (!queue.isEmpty()){
            //将根节点弹出
            TreeNode node = queue.poll();
            if(node!=null){
                sb.append(node.val+",");
                //将左子节点添加进队列
                queue.add(node.left);
                //将右子节点添加到队列
                queue.add(node.right);
            }else{
                sb.append("null,");
            }
        }

        //将最后一个,去掉
        sb.deleteCharAt(sb.length()-1);
        sb.append("]");
        return sb.toString();
    }

    // [1,2,3,null,null,4,5,null,null,null,null]
    public TreeNode deserialize(String data) {
        //将层序遍历的结果反序列化为一颗二叉树
        if(data.equals("[]")) return null;
        //将首尾[]去掉，然后以逗号为空格取出元素
        String[] val = data.substring(1, data.length() - 1).split(",");
        TreeNode root = new TreeNode(Integer.parseInt(val[0]));

        //建立一个队列
        Queue<TreeNode> queue = new LinkedList<>();
        //将根节点入队
        queue.add(root);

        //定义一个变量，遍历数组
        int i=1;

        while (!queue.isEmpty()){
            //将根节点出队
            TreeNode node = queue.poll();

            if(!val[i].equals("null")){
                node.left = new TreeNode(Integer.parseInt(val[i]));
                queue.add(node.left);
            }
            i++;

            if(!val[i].equals("null")){
                node.right = new TreeNode(Integer.parseInt(val[i]));
                queue.add(node.right);
            }
            i++;
        }
        return root;
    }
}

61. 序列化二叉树（层序遍历）

题目：请实现两个函数，分别用来序列化和反序列化二叉树

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过 某种符号表示空节点（#），以 ！ 表示一个结点值的结束（value!）。

二叉树的反序列化是指：根据某种遍历顺序得到的序列化字符串结果str，重构二叉树。

//使用!来分割值value,使用#来代替null值,遇到null的时候添加#!号，遇到数值添加!即可
public class Solution {
    String Serialize(TreeNode root) {
        if(root==null) return "[]";
        StringBuilder sb = new StringBuilder();
        sb.append("[");

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            if(node!=null){
                sb.append(node.val+"!");
                queue.add(node.left);
                queue.add(node.right);
            }else{
                sb.append("#!");
            }
        }

        sb.append("]");
        return sb.toString();

    }
    TreeNode Deserialize(String str) {
        if(str.equals("[]")) return null;
        String[] val = str.substring(1, str.length() - 1).split("!");
        TreeNode root = new TreeNode(Integer.parseInt(val[0]));

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        int i=1;
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            if(!val[i].equals("#")){
                node.left = new TreeNode(Integer.parseInt(val[i]));
                queue.add(node.left);
            }
            i++;

            if(!val[i].equals("#")){
                node.right = new TreeNode(Integer.parseInt(val[i]));
                queue.add(node.right);
            }
            i++;
        }
        return root;
    }
}

60. 把二叉树打印成多行（层序遍历）

题目：从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

代码：

public class Solution {
    ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<>();
        if(pRoot==null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        //将根节点入队
        queue.add(pRoot);

        while (!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<>();
            int len = queue.size();

            for(int i=0;i<=len-1;i++){
                //将根节点出队
                TreeNode node = queue.poll();
                list.add(node.val);

                //将左子节点入队
                if(node.left!=null){
                    queue.add(node.left);
                }
                //将右子节点入队
                if(node.right!=null){
                    queue.add(node.right);
                }
            }
            res.add(list);
        }
       return res;
    }
}

59. 按之字形打印二叉树（层序遍历）

题目：请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

思路：和层序遍历几乎一样，只不过需要定义一个节点变量表示奇数层和偶数层

public class Solution {
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<>();
        if(pRoot==null) return res;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(pRoot);

        //用于区分二叉树是奇数行还是偶数行
        int level = 1;
        while (!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<>();
            int len = queue.size();

            for(int i=0;i<=len-1;i++){
                TreeNode node = queue.poll();
                //如果是奇数行，就将当前节点加入到数组的尾部
                if(level%2==1){
                    list.add(node.val);
                }else{ //如果是偶数行，就将当前节点加入到数组的头部
                    list.add(0,node.val);
                }

                if(node.left!=null){
                    queue.add(node.left);
                }
                if(node.right!=null){
                    queue.add(node.right);
                }
            }
            level++;
            res.add(list);
        }
        return res;
    }
}

58. 对称的二叉树（bfs）

题目：请实现一个函数，用来判断一棵二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

思路：

public class Solution {
    boolean isSymmetrical(TreeNode pRoot) {
        //如果根节点为null，一定是对称的
        if(pRoot==null) return true;

        return dfs(pRoot.left,pRoot.right);
    }

    /**
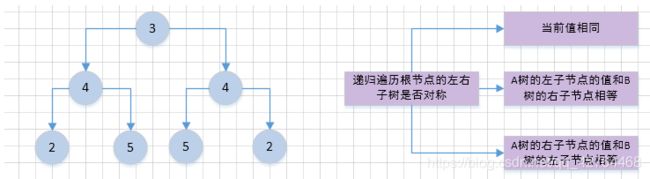
     * 左右子树的结构对称满足三个条件：
     *   1、左右子树的当前节点相同
     *   2、左子树的左节点值和右子树的右节点值相同
     *   3、左子树的右节点值和右子树的左节点值相同
     */
    private boolean dfs(TreeNode left, TreeNode right) {
        if(left == null && right == null) return true;
        if(left == null || right == null) return false;
        return left.val==right.val && dfs(left.left,right.right) && dfs(left.right,right.left);
    }
}

57. 二叉树的下一个节点（线索化）

1、题目：给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

2、思路：

（1）前序遍历：先遍历根节点，再遍历左子节点，最后遍历右子节点

（2）中序遍历：先遍历左子节点，再遍历根节点，最后遍历右子节点

（3）后序遍历：先遍历左子节点，再遍历右子节点，最后遍历根节点

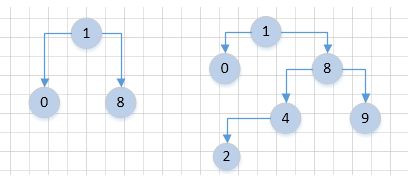
**第1种情况：**当前节点的右子树不为null，比如节点1：

右子树的左子树为null，直接返回当前节点的右子节点：8
右子树不为null，右子树的左子树也不为null，向右子树的左子树深度搜索：2

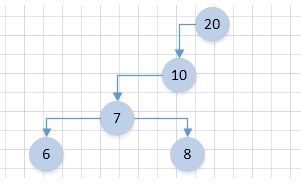
第2种情况： 当前节点的右子树为null，并且当前节点的父节点不为null，比如节点10、6、8

如果当前节点是其父节点的左子节点，就返回当前节点的父节点，比如节点6：7

如果当前接地那是其父节点的右子节点，就返回当前节点的父节点的父节点，比如节点8：10

public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        if(pNode==null) return null;

        //如果当前节点的右子树是不为null
        if(pNode.right!=null){
            pNode = pNode.right;
            while (pNode.left!=null){
                pNode = pNode.left;
            }
            return pNode;
        }
        
        //如果当前节点的右子树都为null，判断当前节点的父节点和父节点的父节点是否为null
        while (pNode.next!=null){
            //获取当前节点的父节点
            TreeLinkNode parentNode = pNode.next;
            //如果当前节点是父节点的左子节点，返回父节点
            if(parentNode.left==pNode){
                return parentNode;
            }
            //否则，返回父节点的父节点
            pNode = parentNode;

        }
        return null;
    }
}

56. 删除排序链表中的重复元素(Leetcode_83)

给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null || head.next==null){
            return head;
        }

        ListNode cur = head;
        while (cur.next!=null){
            if(cur.val == cur.next.val){
                cur.next = cur.next.next;
            }else{
                cur = cur.next;
            }
        }
        return head;
    }
}

56. 删除链表中重复的节点

题目：在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，链表1->2->3->3->4->4->5 处理后为 1->2->5

public class Solution {
    public ListNode deleteDuplication(ListNode pHead) {
        //0--1--2--2--2--3--3--4--5
        if(pHead==null || pHead.next==null) return pHead;
        //在删除节点的时候，我们需要知道该节点的前驱节点，否则删不掉
        //为了保证能够删除头节点，因此定义一个哨兵节点
        ListNode dummy = new ListNode(0);
        dummy.next = pHead;
        ListNode cur = dummy;

        while (cur.next!=null && cur.next.next!=null){
            if(cur.next.val == cur.next.next.val){
                //记录当前链表中第一个开始重复的值
                int temp = cur.next.val;
                //循环删除第一个及之后的重复的值
                while (cur.next!=null && cur.next.val==temp){
                    cur.next = cur.next.next;
                }
            }else{
                cur = cur.next;
            }
        }
        return dummy.next;
    }
}

55. 环形链表（Leetcode_141）

题目：给定一个链表，判断链表中是否有环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

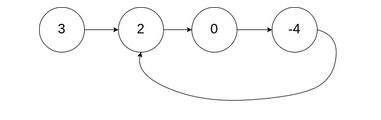
public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head==null || head.next==null) return false;
        //使用快慢指针，让快指针一次走两步，慢指针一次走一步，如果链表成环，那么一定会相遇
        //定义两个指针,一开始指向相同的位置
        ListNode fast = head;
        ListNode slow = head;
		
        //注意是fast.next!=null,防止空指针异常
        while (fast!=null && fast.next!=null){
            
            fast = fast.next.next;
            slow = slow.next;
            
            //如果两者相遇，一定成环
            if(fast == slow) return true;
         
        }
        return false;
    }
}

55.环形链表II（Leetcode_142）

题目：给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

解题思路：https://www.cnblogs.com/hiddenfox/p/3408931.html

第一次相遇时slow走过的距离：a+b，fast走过的距离：a+b+c+b。

因为fast的速度是slow的两倍，所以fast走的距离是slow的两倍，有 2(a+b) = a+b+c+b，可以得到a=c

让两个指针分别从X和Z开始走，每次走一步，那么正好会在Y相遇！也就是环的第一个节点。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        //判断链表是否成环，并找到快慢指针相遇的节点Z
        ListNode fast = head;
        ListNode slow = head;

        while (true){
            //遇到null了，说明链表不成环，返回null
            if(fast==null || fast.next==null){
                return null;
            }

            fast = fast.next.next;
            slow = slow.next;
            
            //快慢指针第一次相遇，即相遇在Z处
            if(slow==fast){
                break;
            }
        }

        //让slow从头开始走，fast接着从Z开始走
        slow = head;
        while (slow != fast){
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}

55. 链表中环的入口节点（快慢指针）

题目：给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

public class Solution {
    public ListNode EntryNodeOfLoop(ListNode pHead) {
        ListNode fast = pHead;
        ListNode slow = pHead;

        while (true){
            if(fast==null || fast.next==null){
                return null;
            }
            fast = fast.next.next;
            slow = slow.next;
            if(fast==slow){
                break;
            }
        }
        slow = pHead;
        while (slow!=fast){
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}

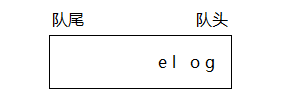
54. 字符流中第一个不重复的字符（队列）

题目：请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符"go"时，第一个只出现一次的字符是"g"。当从该字符流中读出前六个字符“google"时，第一个只出现一次的字符是"l"。如果当前字符流没有存在出现一次的字符，返回#字符。

import java.util.ArrayList;
import java.util.LinkedList;

public class Solution {

    //定义一个数组来记录每个字符出现的次数
    int[] arr = new int[128];

    //定义一个队列存放出现过的字符
    LinkedList<Character> queue = new LinkedList<>();

    //Insert one char from stringstream
    public void Insert(char ch) {
       //统计当前字符出现的次数
        arr[ch] ++;

        if(arr[ch]>1){
            return;
        }

        //如果当前字符已经加入了队列，那就不用再加入队列了，只需要统计出现的次数即可
        //否则加入到队列中
        queue.add(ch);
    }

    //return the first appearence once char in current stringstream
    public char FirstAppearingOnce(){
        //从队列的头部的添加的重复的字符都弹出
        while (!queue.isEmpty() && arr[queue.peek()]>1){
            queue.poll();
        }
        
        if(queue.isEmpty()){
            return '#';
        }
        
        //此时弹出的就是第一个不重复的字符
        return queue.peek();
    }
}

53. 表示数值的字符串

题目：请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100",“5e2”,"-123",“3.1416"和”-1E-16"都表示数值。但是"12e",“1a3.14”,“1.2.3”,"±5"和"12e+4.3"都不是。

public class Solution {
    public boolean isNumeric(char[] str) {
        String s = new String(str);
        if(s.endsWith("F") || s.endsWith("f") || s.endsWith("d")|| s.endsWith("D")){
            return false;
        }
        try {
            //如果转换抛出异常，说明不是数值
            double num = Double.parseDouble(s);
        } catch (NumberFormatException e) {
            return false;
        }
        return true;
    }
}

52. 正则表达式匹配（动态规划）

题目：请实现一个函数用来匹配包括'.'和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（包含0次）。 在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但是与"aa.a"和"ab*a"均不匹配

思路：https://leetcode-cn.com/problems/regular-expression-matching/solution/dong-tai-gui-hua-zen-yao-cong-0kai-shi-si-kao-da-b/

代码：

public class Solution {
    public boolean match(char[] str, char[] pattern) {

        if(str==null || pattern==null) return false;

        //dp[i][j]代表str的前i个字符和pattern的前j个字符是否匹配
        boolean[][] dp = new boolean[str.length+1][pattern.length+1];
        dp[0][0] = true;

        //对于ab---c*ab这种请求后面没有办法考虑到，因此要先初始化(这地方有点难想到)
        for(int i=0;i< pattern.length;i++){
            if(pattern[i]=='*' && dp[0][i-1]){
                dp[0][i+1] = true;
            }
        }

        for(int i=0;i<str.length;i++){
            for(int j=0;j<pattern.length;j++){
                //ab---ab
                if(pattern[j]==str[i]){
                    dp[i+1][j+1] = dp[i][j];
                }
                //ab---a.
                if(pattern[j]=='.'){
                    dp[i+1][j+1] = dp[i][j];
                }

                if(pattern[j]=='*'){
                    //aba---abac*   aba---aba.*
                    if(pattern[j-1]!=str[i] && pattern[j-1]!='.'){
                        dp[i+1][j+1] = dp[i+1][j-1];
                    }else{
                        //aaa---aa*   aba----aa*
                        //aab---aab*
                        //aab---aabb*
                        dp[i+1][j+1] = dp[i][j+1] || dp[i+1][j] || dp[i+1][j-1];
                    }
                }
            }
        }
        return dp[str.length][pattern.length];
    }
}

51. 构建乘积数组（数组）

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。（注意：规定B[0] = A[1] * A[2] * ... * A[n-1]，B[n-1] = A[0] * A[1] * ... * A[n-2];）

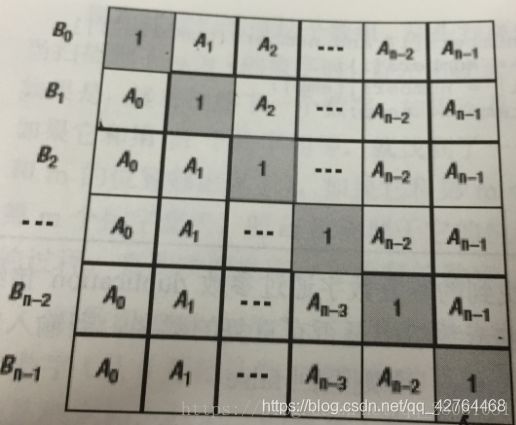
下三角用连乘可以很容易求得，先算下三角中的连乘，即先计算出B[i]中的一部分，然后将上三角中的数也乘进去。这样一来就只需要两个循环就可以解决这个问题。时间复杂度是O(n);

思路：https://blog.csdn.net/qq_28081081/article/details/80875917

先计算下三角每一行的值：下三角从B[0]---B[n-1]
B[0] = 1
B[1] = B[0] * A[0] = 1 * A[0]
B[2] = B[1] * A[1] = 1 * A[0] * A[1]
B[3] = B[2] * A[2] = 1 * A[0] * A[1] *A[2]
...
B[n-1] = B[n-2]*A[n-2] = 1 * A[0] * A[1] *A[2]*...*A[n-2]
再乘以上三角每一行的值：上三角从B[n-2]---B[0]
temp = temp*A[j+1]

代码：

public class Solution {
    public int[] multiply(int[] A) {
        int n = A.length;
        int[] B = new int[A.length];

        B[0] = 1;
        //从下三角矩阵的第二行开始，计算每行下三角值的乘积
        for(int i=1;i<=n-1;i++){
            B[i] = B[i-1] * A[i-1];
        }
        
        int temp = 1;
        for(int j=n-2;j>=0;j--){
            //计算上三角的值
            temp = temp*A[j+1];
            //将上下三角的值乘一起
            B[j] = temp*B[j];
        }
        return B;
    }
}

50. 数组中重复的数字（原地移动）

题目：在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

思路：https://leetcode-cn.com/problems/shu-zu-zhong-zhong-fu-de-shu-zi-lcof/solution/mian-shi-ti-03-shu-zu-zhong-zhong-fu-de-shu-zi-yua/

Leetcode：

class Solution {
    public int findRepeatNumber(int[] nums) {
        int i=0;
        while (i<nums.length){
            if(nums[i] == i){
                i++;
                continue;
            }

            if(nums[nums[i]]==nums[i]) return nums[i];

            //可遍历数组并通过交换操作使元素的 索引 与 值 一一对应（即 nums[i] = i ）。
            // 因而，就能通过索引找到对应的值。
            int temp = nums[i];
            nums[i] = nums[temp];
            nums[temp] =temp;
        }
        return -1;
    }
}

剑指Offer：

public class Solution {
    public boolean duplicate(int numbers[],int length,int [] duplication) {
        if(numbers==null) return false;
        int i=0;
        while (i<numbers.length){
            if(numbers[i]==i){
                i++;
                continue;
            }
            if(numbers[i] == numbers[numbers[i]]) {
                duplication[0] = numbers[i];
                return true;
            }
            //注意：numbers[temp]
            int temp = numbers[i];
            numbers[i] = numbers[temp];
            numbers[temp] = temp;
        }
        return false;
    }
}

49. 把字符串转换为整数（字符串）

题目：请你来实现一个 atoi 函数，使其能将字符串转换成整数。

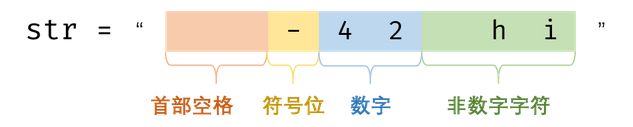
首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。
假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。
该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。在任何情况下，若函数不能进行有效的转换时，请返回 0 。

提示：

本题中的空白字符只包括空格字符 ' ' 。
假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31,  2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。

思路

1、首位空格：字符串前面如果有空格，使用trim()函数去除

2、只包含空格：return 0;

2、符号位：3种情况，即 ‘’+’’ , ‘‘−’’ , ''无符号"，新建一个变量保存符号位，返回前判断正负。

3、数字位：

将字符转换成数字：此 “数字字符的ASCII” 与 “0的ASCII相减”

将字符进行拼接res = 10*res-ascii©-ascii(0)；

代码：

class Solution {
    public int strToInt(String str) {
        //字符串为空
        if(str.length()==0|| str==null) return 0;

        //该函数会根据需要丢弃无用的开头空格字符
        String s = str.trim();

        //字符串仅包含空白字符
        if(s.length()==0) return 0;

        //如果第一位是正负号，那么数字应该从第一位后面的一位开始
        //如果第一位不是正负号，那么数字应该从第一位开始
        int start = 0;

        int sign = 1;
        if(s.charAt(0)=='+'){
            start++;
        }else if(s.charAt(0)=='-'){
            sign = -1;
            start++;
        }

        //定义一个long变量来接收转换后的结果，防止越界
        long res=0;

        //该处理的处理完了，开始将字符串转换为整数
        for(int i=start;i<s.length();i++){
            //判断当前为是否为数字
            if(!Character.isDigit(s.charAt(i))){
                return (int) res*sign;
            }
            
            //开始转换
            res = res*10+s.charAt(i)-'0';
            
            if(res>Integer.MAX_VALUE && sign==1) return Integer.MAX_VALUE;
            if(res>Integer.MAX_VALUE && sign==-1) return Integer.MIN_VALUE;
        }
        return (int) (sign*res);
    }
}

48. 不用加减乘除做加法（^和&）

题目：写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

思路：https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/solution/mian-shi-ti-65-bu-yong-jia-jian-cheng-chu-zuo-ji-7/

class Solution {
    public int add(int a, int b) {
        /**
         * 这题使用位运算来做：s=a+b=c(无进位和)+d(进位和)=e(无进位和)+f(进位和) =...= y(无进位和)+0
         * 由于不能使用加法，因此只能循环使用位运算计算最终的结果，跳出循环的时候就是进位和为0的时候
         * 因为c+d,也属于加法，只能继续e+f，...y+0=a+b
         */
        while (b!=0){
            int c = a ^ b;
            int d = (a & b) <<1;
            a = c;
            b = d;
        }
        return a;
    }
}

47. 求1+2+3+…+n（&&）

求1+2+3+…+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

思路：https://leetcode-cn.com/problems/qiu-12n-lcof/solution/mian-shi-ti-64-qiu-1-2-nluo-ji-fu-duan-lu-qing-xi-/

代码：

public class Solution {
    public int Sum_Solution(int n) {
//        int res = 0;
//        if(n==1) return 1;
//        n = n+Sum_Solution(n-1);
//        return n;
        //要求不能使用if

        //为构成语句，需加一个辅助布尔量 x ，否则会报错；
        //开启递归函数需改写为 Sum_Solution(n - 1) > 0 ，此整体作为一个布尔量输出，否则会报错；
        //前面是Boolean类型，后面也要是Boolean类型
        boolean x=n>1 && (n += Sum_Solution(n-1))>0;
        return n;
    }
}

46. 孩子们的游戏（约瑟夫环）

题目：有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌，然后出圈,从他的下一个小朋友开始,继续0…m-1报数…这样下去…直到剩下最后一个小朋友,可以不用表演。请你试着想下,哪个小朋友会得到这份礼品呢？(注：小朋友的编号是从0到n-1) 。如果没有小朋友，请返回-1

思路：n个人，从第一个人开始报数，m=5，数5下，出圈

利用数组来模拟这个环：

import java.util.ArrayList;
public class Solution {
    public int LastRemaining_Solution(int n, int m) {
        //如果没有小朋友，返回-1
        if(n==0) return -1;
        //利用数组来模拟环
        ArrayList<Integer> list = new ArrayList<>();
        for(int i=0;i<=n-1;i++){
            list.add(i);
        }

        //相当于一个指针指向小朋友
        int index = -1;
        while (list.size()>1){
            //数了count下
            int count = 0;
            while (count<m){
                count++;
                index++;
                if(index==list.size()){
                    index = 0;
                }
            }
            list.remove(index);
            //index指向的小朋友出圈后,index要减1
            index--;
        }
        return list.get(0);
    }
}

43. 左旋转字符串

题目：对于一个给定的字符序列S，请你把其循环左移K位后的序列输出。例如，字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

代码：

public class Solution {
    public String LeftRotateString(String str,int n) {
        //字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。

        if(str==null || str.length()==0) return str;

        StringBuilder sb = new StringBuilder();
        //先把n+1到字符串结尾的元素追加到尾部
        for(int i=n;i<str.length();i++){
            sb.append(str.charAt(i));
        }
        //再把0-n之间的字符追加到末尾
        for(int i=0;i<n;i++){
            sb.append(str.charAt(i));
        }
        return sb.toString();
    }
}

42. 和为S的两个数字（双指针 LeetCode）

题目：输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

思路：https://leetcode-cn.com/problems/he-wei-sde-liang-ge-shu-zi-lcof/solution/mian-shi-ti-57-he-wei-s-de-liang-ge-shu-zi-shuang-/

除了这种方法也可以使用HashMap，但是时间复杂度为O(n)

代码：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        //因为数组是排序的，因此可以使用双指针
        int i=0;
        int j = nums.length-1;
        while (i<j){
            int s = nums[i]+nums[j];
            if(s<target){
                i++;
            } else if(s>target){
                j--;
            }else{
                return new int[]{nums[i],nums[j]};
            }
        }
        return new int[]{0};
    }
}

42. 两数之和（HahMap LeetCode_1）

题目：给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

注意：本题不能使用上面的方法，因为排序后数组元素的系下表就变了，因此需要使用HashMap

public class Solution {
    public int[] twoSum(int[] nums, int target) {
        //使用HashMap，key存放具体的数值，value存放对应的下标
        //查找map中target-nums[i]对应的数值和下标
        HashMap<Integer,Integer> map = new HashMap<Integer, Integer>();
        for(int i=0;i<nums.length;i++){
            if(map.containsKey(target-nums[i])){
                return new int[]{map.get(target-nums[i]),i};
            }
            map.put(nums[i],i);
        }
        return new int[]{0};
    }
}

42. 三数之和（双指针 LeetCode_15）

题目：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。注意：答案中不可以包含重复的三元组。

思路：本题和42题比较像，都是使用双指针但是需要三个数之和，因此需要先固定一个数，然后再使用双指针

https://leetcode-cn.com/problems/3sum/solution/hua-jie-suan-fa-15-san-shu-zhi-he-by-guanpengchn/

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();

        //先对数组进行排序，这个和剑指Offer42题是相同的，只有有序数组才能使用下面的双指针方法
        Arrays.sort(nums);

        //固定一个数nums[i],剩余两个数使用双指针
        for(int i=0;i<nums.length;i++){
            //要求结果不能重复，因此先去重
            if(i>0 && nums[i]==nums[i-1]) continue;

            //左指针
            int left = i+1;
            //右指针
            int right = nums.length-1;

            while (left<right){
                int sum = nums[i]+nums[left]+nums[right];
                if(sum==0){
                    //找到了第一个
                    ans.add(Arrays.asList(nums[i],nums[left],nums[right]));
                    while (left<right && nums[left] == nums[left+1]) left++;
                    while (left<right && nums[right]== nums[right-1]) right--;
                    left++;
                    right--;
                }else if(sum<0){
                    left++;
                }else if(sum>0){
                    right--;
                }
            }
        }
        return ans;
    }
}

42. 四数之和（双指针 LeetCode_18）

题目：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

思路：和三数之和解法相同，没什么大的区别，不同的是，三数之和需要固定一个数，然后使用左右指针，但是四数之和需要固定两个数然后使用左右指针。

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ans = new ArrayList<>();
        Arrays.sort(nums);
        
        for(int i=0;i<nums.length;i++){
            if(i>0 && nums[i]==nums[i-1]) continue;

            for(int j=i+1;j<nums.length;j++){
                if(j>i+1 && nums[j]==nums[j-1]) continue;

                int left = j+1;
                int right = nums.length-1;
                while (left<right){
                    int s = nums[i]+nums[j]+nums[left]+nums[right];
                    if(s==target){
                        ans.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
                        while (left<right && nums[left]==nums[left+1]) left++;
                        while (left<right && nums[right]== nums[right-1]) right--;
                        left++;
                        right--;
                    } else if(s>target){
                        right--;
                    }else{
                        left++;
                    }
                }
            }
        }
        return ans;
    }
}

42. 和为S的两个数（双指针）

题目：输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。对应每个测试案例，输出两个数，小的先输出

public class Solution {
    public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
        ArrayList<Integer> ans = new ArrayList<>();
        //使用双指针，分别指向头部和尾部
        int i=0;
        int j = array.length-1;
        while (i<j){
            int s = array[i]+array[j];
            //相差最远的两个数就是乘积最小的，因此第一个找到的就是最小的
            if(s==sum){
                ans.add(array[i]);
                ans.add(array[j]);
                //找到第一个直接返回
                return ans;
            }else if(s<sum){
                i++;
            }else if(s>sum){
                j--;
            }
        }
        //没找到
        return ans;
    }
}

40. 只出现一次的数字（异或 LeetCode_136）

题目：给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

思路：本题根据题意，线性时间复杂度 O(n)，很容易想到使用 Hash 映射来进行计算，遍历一次后结束得到结果，但是在空间复杂度上会达到 O(n)，需要使用较多的额外空间
既满足时间复杂度又满足空间复杂度，就要提到位运算中的异或运算 XOR，主要因为异或运算有以下几个特点：

一个数和 0 做 异或 运算等于本身：a⊕0 = a
一个数和其本身做 异或 运算等于 0：a⊕a = 0
异或运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b

代码：

class Solution {
    public int singleNumber(int[] nums) {
        //位运算，异或运算
        //a⊕0 = a
        //a⊕a = 0
        //a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
        //除了一个元素外，其他元素都出现两次，那么那些出现两次的元素异或后结果就为0
        int res = 0;
        for(int i=0;i<nums.length;i++){
            res = res ^ nums[i];
        }
        return res;
    }
}

40. 只出现一次的数字（HashMap LeetCode_137）

题目：给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

class Solution {
    public int singleNumber(int[] nums) {
        HashMap<Integer,Integer> map = new HashMap();

        for(int i=0;i<=nums.length-1;i++){
            if(!map.containsKey(nums[i])){
                map.put(nums[i],1);
            }else{
                map.put(nums[i],map.get(nums[i])+1);
            }
        }

        //获取key的集合
        Set<Integer> set = map.keySet();
        //通过Key获取value
        for(Integer key:set){
           if(map.get(key)==1){
               return key;
           }
        }
        return 0;
    }
}

40. 只出现一次的数字（异或）

题目：一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。

分析：

一个数和 0 做 异或 运算等于本身：a⊕0 = a
一个数和其本身做 异或 运算等于 0：a⊕a = 0
异或运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b

由于数组中存在着两个数字不重复的情况，我们将所有的数字异或操作起来，最终得到的结果是这两个数字的异或结果，最后结果一定不为0，因为有两个数字不重复。

问题是我们得出的是最后的两个数异或后的结果，但是无法通过异或结果111来得出最终的两个不同的数,比如：

4 ^ 1 ^ 4 ^ 6 => 1 ^ 6

6 对应的二进制： 110
1 对应的二进制： 001
1 ^ 6  二进制： 111

通过 & 运算来判断一位数字不同即可分为两组，那么我们随便两个不同的数字至少也有一位不同吧！
我们只需要找出任意一位不同的数字，即可完成分组操作。

由于两个数异或的结果就是两个数数位不同结果的直观表现，所以我们可以通过异或后的结果去找一位不同的数字mask，所有的可行 mask 个数，都与异或后1的位数有关。只要异或后的位数为1，就可作为分组条件，就说明两个数可以分到两个不同的组。

num1:       101110      110     1111
num2:       111110      001     1001
num1^num2:  010000      111     0110

可行的mask:  010000      001     0010
                        010     0100
                        100     

为了操作方便，我们只去找最低位的mask:

num1^num2
		k:  010000 
  &
     mask:  000001
     		000000
     mask:  000010
     		000000
     mask:	000100
     		000000
     mask:	001000
     		000000
     mask:	010000
    		000000
     mask:  010000	:根据mask的1对应的位将数组中的数分成两组，在这位上为0的分到一组，为1的分到1组
     
     num1:	101110	：mask为1的位上为0
     num2:	111110	：mask为1的位上为1

代码：

//num1,num2分别为长度为1的数组。传出参数
//将num1[0],num2[0]设置为返回结果
public class Solution {
    public void FindNumsAppearOnce(int [] array,int num1[] , int num2[]) {
        //存放异或结果
        int  k= 0;

        //求出数组中所有数异或的结果
        for(int i=0;i<array.length;i++){
            //0与任何数异或都是他本身：0^array[0]^array[1]^array[2]...^array[n-1]
            k = k^array[i];
        }

        // 00000001
        int mask = 1;

        //求出最低位的mask
        while ((k&mask)==0){
            //让mask左移一位
            mask = mask << 1;
        }

        num1[0] = 0;
        num2[0] = 0;

        //遍历数组，让mask为1时对应数位为0的一组的数异或，让mask为1时对应数位为1的一组的数异或
        for(int i=0;i<array.length;i++){
            if((array[i] & mask)==0){
                num1[0] = num1[0] ^ array[i];
            }else{
                num2[0] = num2[0] ^ array[i];
            }
        }
    }
}

40. 只出现一次的数字（异或 LeetCode_260）

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。

class Solution {
    public int[] singleNumber(int[] nums) {
        //遍历数组，求出所有数字的异或结果
        int k=0;
        for(int i=0;i<nums.length;i++){
            k = k^nums[i];
        }

        //求出mask
        int mask = 1;
        while ((k&mask)==0){
            mask = mask << 1;
        }

        int a = 0;
        int b = 0;

        for(int i=0;i<nums.length;i++){
            if((mask & nums[i])==0){
                a = a^ nums[i];
            }else{
                b = b ^ nums[i];
            }
        }
        return new int[]{b,a};
    }
}

39. 平衡二叉树

题目： 输入一棵二叉树，判断该二叉树是否是平衡二叉树。 在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树

分析：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。高度就是层数

https://leetcode-cn.com/problems/balanced-binary-tree/solution/balanced-binary-tree-di-gui-fang-fa-by-jin40789108/

public class Solution {
    public boolean IsBalanced_Solution(TreeNode root) {
        if(root == null) return true;
        //判断当前子树是否是平衡树； && 判断当前子树的左子树是否是平衡树；&& 判断当前子树的右子树是否是平衡树；
        if(Math.abs(depth(root.left)-depth(root.right))<=1
                && IsBalanced_Solution(root.left)
                && IsBalanced_Solution(root.right)){
            return true;
        }
        return false;
    }

    // 求二叉树的深度，前序遍历
    private int depth(TreeNode root) {
        if(root ==null) return 0;
        //递归遍历左子树,求左子树的高度
        int leftHeight = depth(root.left);
        //递归遍历右子树，求右子树的高度
        int rightHeight = depth(root.right);
        return Math.max(leftHeight,rightHeight)+1;
    }
}

38. 二叉树的深度

题目：输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root ==null) return 0;
        int leftHeight = TreeDepth(root.left);
        int rightHeight = TreeDepth(root.right);
        return Math.max(leftHeight,rightHeight)+1;
    }
}

37. 在排序数组中查找元素的第一个和最后一个位置（Leetcode_34）

**题目：**给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。你的算法时间复杂度必须是 O(log n) 级别。如果数组中不存在目标值，返回 [-1, -1]。

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums==null || nums.length==0) return new int[]{-1,-1};

        //寻找第一个位置
        int start = findFirst(nums,target);
        if(start==-1) return new int[]{-1,-1};

        //寻找最后一个位置
        int end = findEnd(nums,target);
        return new int[]{start,end};
    }

    private int findFirst(int[] nums, int target) {
        int start = 0;
        int end = nums.length-1;
        //二分查找
        while (start+1<end){
            int mid = (end-start)/2+start;
            if(target>nums[mid]){
                start = mid;
            }else{
                end = mid;
            }
        }
        //先返回start再返回end
        if(nums[start]==target) return start;
        if(nums[end] == target) return end;
        return -1;
    }

    private int findEnd(int[] nums, int target) {
        int start = 0;
        int end = nums.length-1;
        //二分查找
        while (start+1<end){
            int mid = (end-start)/2+start;
            //多个等号
            if(target>=nums[mid]){
                start = mid;
            }else{
                end = mid;
            }
        }
        //先返回end，再返回start
        if(nums[end] == target) return end;
        if(nums[start]==target) return start;
        return -1;
    }
}

37. 数字在排序数组中出现的次数（二分查找）

题目：统计一个数字在排序数组中出现的次数。

public class Solution {
    public int GetNumberOfK(int [] array , int k) {
        if(array.length==0 || array==null) return 0;

        //找出初始索引
        int start = findFirst(array, k);
        if(start==-1) return 0;
        
        //找出最后索引
        int end = findEnd(array, k);
        return end-start+1;
    }

    private int findFirst(int[] nums, int target) {
        //二分查找
        int start = 0;
        int end = nums.length-1;
        while (start+1<end){
            //二分的mid
            int mid = (end-start)/2+start;
            //如果target在mid的右边
            if(target>nums[mid]){
                start = mid;
            }else{
                end = mid;
            }
        }
        //先返回start，再返回end
        if(nums[start]==target) return start;
        if(nums[end]==target) return end;
        return -1;
    }

    private int findEnd(int[] nums, int target) {
        int start = 0;
        int end = nums.length-1;
        //二分查找
        while (start+1<end){
            int mid = (end-start)/2+start;
            //多个等号
            if(target>=nums[mid]){
                start = mid;
            }else{
                end = mid;
            }
        }
        //先返回end，再返回start
        if(nums[end] == target) return end;
        if(nums[start]==target) return start;
        return -1;
    }
}

36. 两个链表的第一个公共节点

题目：输入两个链表，找出它们的第一个公共结点。

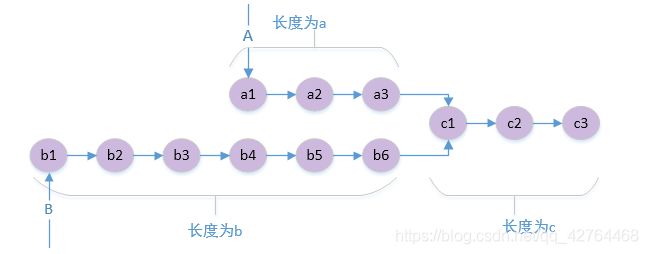
思路：两个指针，一个指针指向A，一个指针指向B，让他们遍历两个链表，每遍历一个节点就比较一次，判断是不是相等，相等就退出循环，如果A先走到链表的尾部，就从B链表的头开始走，如果B走到了链表的尾部，从A链表的头开始走，最终两个指针一定会相遇在第一个公共节点。

指针A走过的路径：a+c+b

指针B走过的路径：b+c+a ，两者最终相遇在第一个公共节点处

public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        if(pHead1 == null || pHead2 == null) return null;

        //定义两个指针用来遍历链表
        ListNode cur1 = pHead1;
        ListNode cur2 = pHead2;

        while (cur1!=cur2){
            if(cur1==null){
                cur1 = pHead2;
            }else{
                cur1 = cur1.next;
            }

            if(cur2==null){
                cur2 = pHead1;
            }else{
                cur2 = cur2.next;
            }
        }
        return cur1;
    }
}

34. 第一个只出现一次的字符

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.（从0开始计数）

方法1：使用数组统计次数：

public class Solution {
    public int FirstNotRepeatingChar(String str) {
        int[] ans = new int[128];

        char[] array = str.toCharArray();

        //统计每个字符出现的次数
        for(int i=0;i<array.length;i++){
            ans[array[i]]++;
        }

        for(int i=0;i<array.length;i++){
            if(ans[array[i]]==1){
                return i;
            }
        }
        return -1;
    }
}

方法2：使用hashmap统计次数

public class Solution {
    public int FirstNotRepeatingChar(String str) {
        HashMap<Character,Integer> map = new HashMap<>();
        char[] array = str.toCharArray();

        for(int i=0;i<array.length;i++){
            if(map.containsKey(array[i])){
                map.put(array[i],map.get(array[i])+1);
            }else{
                map.put(array[i],1);
            }
        }

        for(int i=0;i<array.length;i++){
            if(map.get(array[i])==1){
                return i;
            }
        }
        return -1;
    }
}

33. 丑数（动态规划）

题目：把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

思路：https://leetcode-cn.com/problems/chou-shu-lcof/solution/mian-shi-ti-49-chou-shu-dong-tai-gui-hua-qing-xi-t/

public class Solution {
    public int GetUglyNumber_Solution(int index) {

        if(index<=0){
            return 0;
        }

        //代表第index+1个丑数
        int[] dp = new int[index];
        //第一个丑数为1
        dp[0] = 1;

        int a = 0;
        int b = 0;
        int c = 0;

        for(int i=1;i<index;i++){
            dp[i] = Math.min(Math.min((dp[a]*2),(dp[b]*3)),(dp[c]*5));

            //更新索引
            if(dp[i] == dp[a]*2){
                a++;
            }
            if(dp[i] == dp[b]*3) {
                b++;
            }
            if(dp[i] == dp[c]*5){
                c++;
            }
        }
        return dp[index-1];
    }
}

32. 把数组排成最小的数（自定义排序）

题目：输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

import java.util.Arrays;
import java.util.Comparator;

public class Solution {
    public String PrintMinNumber(int [] numbers) {
        //把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。
        //将数组转换为字符串，让后遍历字符串，两个比较
        //如果s1+s2

        //1、首先将整型数组转换为字符串数组
        String[] str = new String[numbers.length];
        for(int i=0;i<numbers.length;i++){
            str[i] = String.valueOf(numbers[i]);
        }

        //2、定义字符串字符串数组内的字符排除规则
        Arrays.sort(str, new Comparator<String>() {
            //比如 30 5，取值时按照序列逆着取，o1=5,o2=30
            //如果返回1，不交换顺序，还是30 5
            //如果返回-1，交换顺序，5 30
            @Override
            public int compare(String o1, String o2) {
                return (o1+o2).compareTo(o2+o1);
            }
        });

        //3、将字符串数组编程字符串
        StringBuilder sb = new StringBuilder();
        for(int i=0;i<numbers.length;i++){
            sb.append(str[i]);
        }
        return sb.toString();
    }
}

31. 整数中1出现的次数 (递归)

题目：输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

思路：https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/javadi-gui-by-xujunyi/

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        return f(n);
    }

    private int f(int n) {
        if(n<=0) return 0;
        String str = String.valueOf(n);
        //求数字的最高位
        int high = str.charAt(0)-'0';
        int pow = (int) Math.pow(10,str.length()-1);
        int last = n-high*pow;

        if(high==1){
            //比如1234：high=1,pow=1000,last=234
            //1--999中1的个数：f(pow-1)
            //1000-1234中：只看最高位1，不看其他位1时，那么1的个数为：last+1 (0-234)
            //1000-1234中：不看最高位1，只看其他位1时，那么1的个数为：f(last)
          return f(pow-1) + f(last) + last+1;
        }else{
            //比如2345：high=2,pow=1000,last=345
            //1--999中1的个数：f(pow-1)
            //1000--1999中：只看最高位1，不看其他位1时，那么1的个数为：pow
            //1000--1999中：不看最高位1，只看其他位1时，那么1的个数为：f(pow-1)
            //2000--2345中：f(last)
            return f(pow-1)*high + f(last) + pow;
        }
    }
}

30. 连续子数组的最大和(动态规划)

题目：输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。

**思路：**动态规划解法

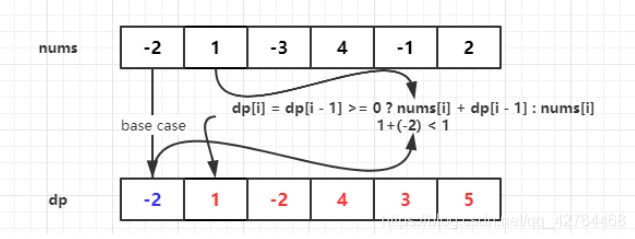
此处的状态转移方程也可以切换为 dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
因为是需要最大和的连续子数组，因此可以保存每个数组元素所在位置能够得到的最大连续元素和，这个最大值可以通过判断前一个最大值是否为负数来判断（因为负数无论加任何数都比当前数小），如果为负，当前元素的最大和就是其本身。

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if(array.length==0 || array==null) return 0;

        //创建dp表,dp[i]代表前i个数的和
        int[] dp = new int[array.length];
        dp[0] = array[0];
        int res = dp[0];

        for(int i=1;i<array.length;i++){
            dp[i] = dp[i-1]>0 ?dp[i-1]+array[i]:array[i];
            res =  Math.max(dp[i],res);
        }
        return res;
    }
}

29. 最小的K个数（快排/大顶堆）

题目：输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

方法1：大顶堆（堆顶的元素比其他元素要大）

本题是求前 K 小，因此用一个容量为 K 的大根堆，每次 poll 出最大的数，那堆中保留的就是前 K 小啦（注意不是小根堆！小根堆的话需要把全部的元素都入堆，那是 O(NlogN)，就不是 O(NlogK)了）

public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        //空值判断
        ArrayList<Integer> list = new ArrayList<>();
        if(input==null || input.length==0 || input.length<k || k<=0) return list;

        //定义一个大顶堆
        PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;
            }
        });

        for(int i=0;i<input.length;i++){
            //如果队列中的数小于k个，就添加进队列
            if(queue.size()<k){
                queue.add(input[i]);
            //如果大于k个，就判断要添加的数是否比堆顶的数小，如果小的话就将堆顶的数弹出，将当前树添加进去
            }else if(input[i]<queue.peek()){
                queue.poll();
                queue.add(input[i]);
            }
        }

        int size = queue.size();
        for(int i=0;i<size;i++){
            list.add(0,queue.poll());
        }
        return list;
    }
}

方法2：快速排序

28. 数组中出现次数超过一半的数字（LeetCode）

题目：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。

方法1：排序算法，排序后数组的中位数一定是众数

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length/2];
    }
}

方法2：摩尔投票法

class Solution {
    public int majorityElement(int[] nums) {
        //众数
        int mianNum = 0;
        //票数
        int votes = 0;

        for(int i=0;i<nums.length;i++){
            if(votes==0){
                //如果前面的数，票数正负抵消了，就让当前的数作为众数
                mianNum = nums[i];
            }
            //统计票数
            if(nums[i]==mianNum){
                votes ++;
            }else{
                votes --;
            }
        }
        return mianNum;
    }
}

28. 数组中出现次数超过一半的数字

题目：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果该数不存在，返回0

方法1：排序后的中位数就是众数

import java.util.Arrays;
public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        Arrays.sort(array);

        //判断中位数是不是众数
        int count = 0;
        for(int i=0;i<array.length;i++){
            if(array[i]==array[array.length/2]){
                count++;
            }
        }
        return count>array.length/2 ? array[array.length/2]:0;
    }
}

方法2：摩尔投票法

public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
       int mianNum =0;
       int votes = 0;
       for(int i=0;i<array.length;i++){
           if(votes==0){
               mianNum = array[i];
           }
           if(array[i]==mianNum){
               votes++;
           }else{
               votes--;
           }
       }

        //判断该数是不是众数
        int count = 0;
        for(int i=0;i<array.length;i++){
            if(array[i]==mianNum){
                count++;
            }
        }
        return count>array.length/2 ? mianNum:0;
    }
}

27. 全排列（LeetCode_46）

题目：给定一个 没有重复 数字的序列，返回其所有可能的全排列。

递归回溯算法模板：

public void dfs(路径，选择列表){
	if (满足结束条件){
		result.add(路径)
		return;
	}
	for(遍历数组，即选择列表){
		1、排除掉不合法的选择
		2、做选择：路径.add(选择)
		3、dfs(路径，选择列表)遍历下一层树
		4、撤销选择：路径.remove(选择)
	}
}

代码：

class Solution {
    //存放最终的组合结果
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        //选择的路径，即一种组合
        List<Integer> path = new ArrayList<>();

        if(nums==null || nums.length==0){
            return res;
        }

        //定义一个布尔类型的数组,用于判断树的每一层的数据有没有选择过
        boolean[] used = new boolean[nums.length];
        dfs(nums,used,path);
        return res;
    }
    
    private void dfs(int[] nums, boolean[] used, List<Integer> path) {
        //找到了符合条件的结果
        if(nums.length==path.size()){
           res.add(new ArrayList<>(path));
           return;
        }

        //遍历数组,即遍历选择列表
        for(int i=0;i<nums.length;i++){
            //排除掉不合法的情况
            if(used[i]){
                continue;
            }
            //做出选择
            used[i] = true;
            path.add(nums[i]);

            dfs(nums,used,path);

            //撤销选择
            used[i] = false;
            path.remove(path.size()-1);
        }
    }
}

27. 全排列（LeetCode_47）

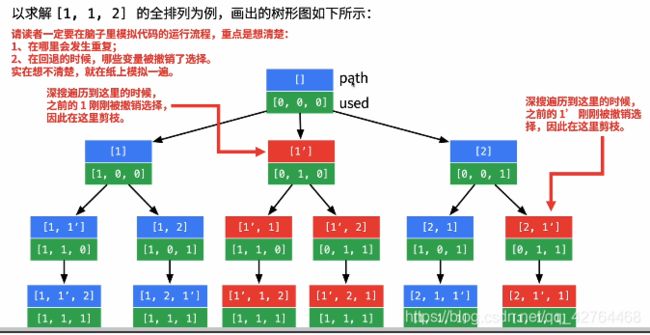
给定一个可包含重复数字的序列，返回所有不重复的全排列。

https://leetcode-cn.com/problems/permutations-ii/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liwe-2/

public void dfs(路径，选择列表){
	if (满足结束条件){
		result.add(路径)
		return;
	}
	for(遍历数组，即选择列表){
		1、排除掉不合法的选择
		2、做选择：路径.add(选择)
		3、dfs(路径，选择列表)遍历下一层树
		4、撤销选择：路径.remove(选择)
	}
}

代码：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<Integer> path = new ArrayList<>();
        if(nums.length==0 || nums==null){
            return res;
        }
        boolean[] used = new boolean[nums.length];
        //对数组进行排序，方便剪枝,如果不排序无法剪枝
        Arrays.sort(nums);
        dfs(nums,path,used);
        return res;
    }

    private void dfs(int[] nums, List<Integer> path, boolean[] used) {
        //如果满足条件，添加到结果集合中
        if(path.size()==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }

        //遍历选择列表
        for(int i=0;i<nums.length;i++){
            //排除掉不合法的选择
        //1、已经选择过的就不再选择
        if(used[i]){
            continue;
        }

        //2、如果当前这个数和前一个数相等，并且前面那个数刚撤销选择，也不再选择
        if(i>0 && nums[i]==nums[i-1] && used[i-1]){
            continue;
        }

        //做出选择
        used[i] = true;
        path.add(nums[i]);

        dfs(nums,path,used);

        //撤销选择
        used[i] = false;
        path.remove(path.size()-1);
    }
}

27. 字符串的排列（递归回溯）

题目：输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/solution/hui-su-suan-fa-java-by-liweiwei1419/

输入一个字符串，打印出该字符串中字符的所有排列。你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

递归回溯算法：

public void dfs(路径，选择列表){
	if (满足结束条件){
		result.add(路径)
		return;
	}
	for(遍历数组，即选择列表){
		1、排除掉不合法的选择
		2、做选择：路径.add(选择)
		3、dfs(路径，选择列表)遍历下一层树
		4、撤销选择：路径.remove(选择)
	}
}

代码：

class Solution {
    ArrayList<String> res = new ArrayList<>();
    public String[] permutation(String s) {
        //初值判断
        if(s.length()==0 || s==null){
            return res.toArray(new String[0]);
        }
        //选择列表
        char[] array = s.toCharArray();
        Arrays.sort(array);

        boolean[] used = new boolean[array.length];
        StringBuilder path = new StringBuilder();

        dfs(array,path,used);
        return res.toArray(new String[0]);
    }

    private void dfs(char[] array, StringBuilder path, boolean[] used) {
        //如果已经找到了一个结果，添加进res
        if(array.length==path.length()){
            res.add(path.toString());
            return;
        }

        for(int i=0;i<array.length;i++){
            //排除掉不合法的选择
            if(used[i]){
                continue;
            }

            if(i>0 && array[i]== array[i-1] && used[i-1]==false){
                continue;
            }

            //做出选择
            used[i] = true;
            path.append(array[i]);

            dfs(array,path,used);

            //撤销选择
            used[i] = false;
            path.deleteCharAt(path.length()-1);
        }
    }
}