Codeforces Round #621 (Div. 1 + Div. 2)_B. Cow and Friend(C++_数论)
Bessie has way too many friends because she is everyone’s favorite cow! Her new friend Rabbit is trying to hop over so they can play!
More specifically, he wants to get from (0,0) to (x,0) by making multiple hops. He is only willing to hop from one point to another point on the 2D plane if the Euclidean distance between the endpoints of a hop is one of its n favorite numbers: a1,a2,…,an. What is the minimum number of hops Rabbit needs to get from (0,0) to (x,0)? Rabbit may land on points with non-integer coordinates. It can be proved that Rabbit can always reach his destination.
Recall that the Euclidean distance between points (xi,yi) and (xj,yj) is ( x i − x j ) 2 + ( y i − y j ) 2 \sqrt{(xi−xj)^2+(yi−yj)^2} (xi−xj)2+(yi−yj)2
For example, if Rabbit has favorite numbers 1 and 3 he could hop from (0,0) to (4,0) in two hops as shown below. Note that there also exists other valid ways to hop to (4,0) in 2 hops (e.g. ( 0 , 0 ) → ( 2 , 5 ) → ( 4 , 0 ) ) (0,0) → (2,\sqrt{5}) → (4,0)) (0,0)→(2,5)→(4,0)).
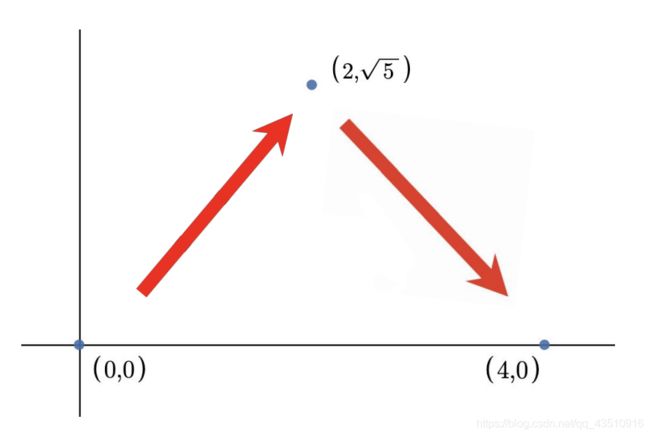
Here is a graphic for the first example. Both hops have distance 3, one of Rabbit’s favorite numbers.
In other words, each time Rabbit chooses some number ai and hops with distance equal to ai in any direction he wants. The same number can be used multiple times.
Input
The input consists of multiple test cases. The first line contains an integer t (1≤t≤1000) — the number of test cases. Next 2t lines contain test cases — two lines per test case.
The first line of each test case contains two integers n and x (1≤n≤105, 1≤x≤109) — the number of favorite numbers and the distance Rabbit wants to travel, respectively.
The second line of each test case contains n integers a1,a2,…,an (1≤ai≤109) — Rabbit’s favorite numbers. It is guaranteed that the favorite numbers are distinct.
It is guaranteed that the sum of n over all the test cases will not exceed 105.
Output
For each test case, print a single integer — the minimum number of hops needed.
Example
input
4
2 4
1 3
3 12
3 4 5
1 5
5
2 10
15 4
output
2
3
1
2
Note
The first test case of the sample is shown in the picture above. Rabbit can hop to ( 2 , 5 ) (2,\sqrt{5}) (2,5), then to (4,0) for a total of two hops. Each hop has a distance of 3, which is one of his favorite numbers.
In the second test case of the sample, one way for Rabbit to hop 3 times is: (0,0) → (4,0) → (8,0) → (12,0).
In the third test case of the sample, Rabbit can hop from (0,0) to (5,0).
In the fourth test case of the sample, Rabbit can hop: ( 0 , 0 ) → ( 5 , 10 2 ) → ( 10 , 0 ) (0,0) → (5,10\sqrt{2}) → (10,0) (0,0)→(5,102)→(10,0).
Process
这个题有俩坑,我先说下大概思路吧:
1.找最大值;
2.如果在遍历的时候恰好遇到与路径长度相等的喜欢的数,就直接输出1;
3.如果没有相等的,那么最大值大于要走的路,输出2;
4.如果最大值小于要走的路,就看要走几个最大值才能到终点,也就是向上取整!
Code
#include