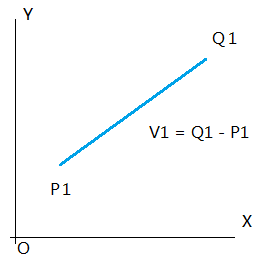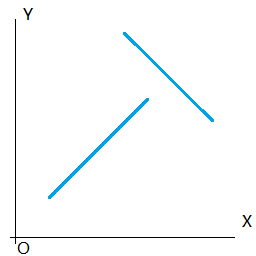谁说数学没用——基元碰撞检测(1)
这里介绍的是“基元”之间的碰撞检测,所谓“基元”就是线段、三角形、矩形、平面、圆、椭圆等各种常见的、能用一两个数学公式表示的图形。“基元碰撞检测”是游戏开发中常用的手段,用数学公式求解碰撞结果,能让我们系统性的理解其中的原理。大家也不用担心,里面用到的数学公式,充其量高中、大一都学过,都属于“空间解析几何”范畴。
----------------------------------------------- 华丽的分割线 -----------------------------------------------
好接下来开始最简单的,“2D线段”与“2D线段”之间的碰撞检测。注意这里是“线段”,不是“直线”或者“射线”,如果搞不清的,建议先搜索一下。
先说结果:
1. 两根“线段”之间如果有正常的“相交”,那么结果应该是一个点。
2. 在以下情况下没有交点:平行、但不重合;在很远处相交,不在线段范围内。
3. 如果重合,我们需要特殊处理。
假设在2D坐标系中,有一条线段,如下图所示:
起点为P1,坐标为(Xp1, Yp1)
终点为Q1,坐标为(Xq1,Yq1)
那么从P1到Q1有一个向量V1,可以表示为 V1 = Q1 - P1,反过来,Q1 = P1 + V1。这个应该很好理解。
好,接下来,对于该线段上任意一个点P,我们可以用如下“参数方程”表示:
P = P1 + t * V1 t ∈ [0, 1]
把V1 = Q1 - P1替代进去,我们可以得到:
P = P1 + t * (Q1 - P1) t ∈ [0, 1]
见下图
其中t为变参,它的范围是0~1,两边都是闭区间,我们可以把它理解为0~100的一个百分比。
当 t=0 的时候,P = P1 + 0 * V1, --> P = P1,即P点与P1点重合。
当 t=1 的时候,P = P1 + 1 * V1, --> P = P1 + V1 = P1 + (Q1 - P1) = Q1,即P点与Q1点重合。
如果 t=0.5,P = P1 + 0.5 * (P2 - P1) = 0.5 * (P2 + P1),即线段的中点,就是50%的位置。
如果t超出这个范围,那么点虽然在该线段所处的直线上,但“不在线段范围内”。如下图,t > 1
接下来我们把第二根线段放进去,P2 -> Q2,我们可以得到:
V2 = Q2 - P2
P = P2 + s * V2 s ∈ [0, 1]
P = P2 + s * (Q2 - P2) s ∈ [0, 1]
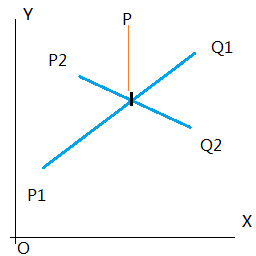
大家注意两根线段的“参数方程”有点小区别,我们在第一个方程中用了变参 t,在第二个方程中用了变参 s,以此表示两个不同的变量,切不可都写成 t,否则最后联立方程组的时候,会傻傻分不清楚。(仔细想想为什么?)
----------------------------------------------- 华丽的分割线 -----------------------------------------------
假设两根线段相交于点P,那么:
P = P1 + t * V1 t ∈ [0, 1]
P = P2 + s * V2 s ∈ [0, 1]
两个等式左边都是P,那么我们可以令他们相等:
P1 + V1 * t = P2 + V2 * s
把等式处理一下,得到:
t * V1 – s * V2 = P2 – P1
因为每个点其实有两个坐标值(x,y),我们可以得到:
t * V1.x – s * V2.x = (P2 – P1).x = P12.x
t * V1.y – s * V2.y = (P2 – P1).y = P12.y
哈,现在我们就有两个方程,构成一个方程组,来求解两个变量了。如果到这里,你已经会继续处理了(比如消元法、代入法),那就不用继续往下看了,下面我用行列式(线性代数)来求得 t 和 s 。
----------------------------------------------- 华丽的分割线 -----------------------------------------------
| V1.y V2.y |
如果线性代数还有点印象的话,对此应该能理解,行列式不是矩阵,行列式虽然写起来跟矩阵差不多、有一大堆值,但其实它的结果就是一个数值:
A = V1.x * V2.y - V2.x * V1.y 左上 * 右下 - 右上 * 左下
继续:
T = | P12.x V2.x | S = | V1.x P12.x || P12.y V2.y | | V1.y P12.y |
T = P12.x * V2.y - V2.x * P12.y S = V1.x * P12.y - P12.x * V1.y
最终结果:
{ t = T / A
{ s = S / A
再回过来看方程, P = P1 + V1 * t = P2 + V2 * s,说明线段1在 t比例 处与线段2相交,这个位置是线段2的 s比例 处。
A = V1.x * V2.y - V2.x * V1.y = 0
V1.x * V2.y = V2.x * V1.y
V2.y / V2.x = V1.y / V1.x
y/x,结果就是这根线段或直线的“斜率”。如果两根线段的“斜率”相等,那可不就是“平行”或“重合”吗?所以,算完 A,先别着急算 T 和 S,如果A = 0,那函数可能就要返回False了,认为没有相交。
如果A不等于0,就可以继续得到 t 和 s。接着我们要判断 t 和 s的范围,前面我们说过,t ∈ [0, 1] && s ∈ [0, 1],才是相交在两个线段范围内,如果任一条件不满足,仍然不是“线段相交”,而是“直线相交”或“射线相交”。
----------------------------------------------- 华丽的分割线 -----------------------------------------------
原理讲完了,求解部分的伪代码如下:
A = V1.x * V2.y - V2.x * V1.y
if (A == 0) return Parallel Or SuperPosition;
T = P12.x * V2.y - V2.x * P12.y
t = T / A
if ( t < 0 || t > 1 ) return No Intersection;
S = V1.x * P12.y - P12.x * V1.y
s = S / A
if ( s < 0 || s > 1 ) return No Intersection;
P = P1 + t * V1
return P; // P就是最终交点