基于Huffman 和 LZ77的文件压缩(五)收尾
点我看LZ77代码
压缩好了,就知道文件怎么存了
解压缩就超级简单了。
获取标记文件,判断比特位0还是1
遇见0直接解压缩
遇见0向前匹配DIST距离,找LEN长度。
解决 大于64K文件的压缩
针对上一篇无法解决64K以上文件也很好解决。
在读取文件后解决时,每次只需判断一下缓冲区的剩余数据够不够MIN_MATCH
不够的话从文件中读取WSIZE个,
那么在读取之前,先讲先行缓冲区窗口内的数据搬移到查找缓冲区,
同时更新哈希表中的位置数据,和冲突数据
直到读取到文件尾。
压缩效率
遇到的问题
1 缓冲区错用了char ,char不能会出现下标为负数的情况,导致数组下标越界。
2 寻找最长匹配的时候错用了UCH导致部分解码失败UCH接收256~258时发生错误,长度应该用USH接收,因为我们匹配为3~258
3 写压缩文件和解压缩时文件指针类型刚开始写的时普通类型,后期发现导致汉字出现乱码,解决方式:让文件指针以二进制方式
4 解压缩时,未及时刷新缓冲区,错将fflush(文件指针)写成fflush(stdout)
PS 这个错误导致我找错找了1天多。。哭死了~ 这下长记性了吧?
对LZ77 的压缩结果再压缩,效率就不怎么好了。
能否采用Huff曼的方式直接对LZ77结果再压缩?
**可以 ,但压缩率可能不是很好;
1 Huffman缺陷 :需要创建哈夫曼树,可能会很大
2 LZ77的标记信息也会参与Huffman压缩,因此,影响压缩率。
3 树大的话,内存可能压力比较大。
假设文件中含有200个不同种类的字节,
那么 总节点将是叶子结点200 +临时父亲199个 = 399个节点。即2n -1。
那么Huffman树就很大了 ,获取编码的效率就比较低了。
获取编码的方式: 递归到叶子。
解决方案: 范式哈夫曼树

范式哈夫曼树: 在哈夫曼树的基础上,做了强制约定:
1 同一层节点中,所有的叶子节点都调整的左边
2 同一层节点,按照符号从小到达调整
1 同层编码递增ADG:00 01 10 (方式+1)
2 不同层编码推导方式:
上一层最后一个编码+1 ,再左移层数差 例如下图的 G 和 H
G 10
H 10 +1 -->11 再左移一位110
计算每个节点编码,得知道码字长度(高度)
范式哈夫曼树创建过程(编码获取过程)
其实没必要构建,直接处理哈夫曼树就行了
1 模拟哈夫曼树的创建(用静态数组就行)
a 遍历文件,获取每个字符的出现频度
b 创建静态数组,容量 叶子数*2 -1
即 2n -1;
c 前n 个位置保存叶子

即用数组下标代替指针的链接关系(双亲指针)
1 每次取一个节点,通过parent(下标)直到根节点就可以获取编码长度了
2 排序:
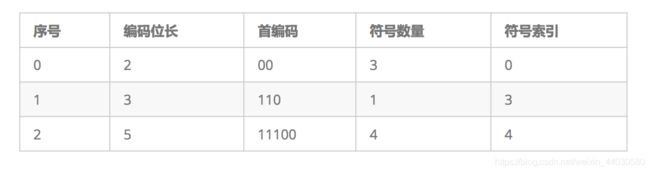
以码长为第一关键字,字符序号为第二关键字排序,得到一个序列(编码长度表)
3 根据编码长度表,获取每个符号的编码(可见范式Huffman树和哈夫曼树的**编码长度**一致)
4 根据编码,重新改写文件
**编码长度表:**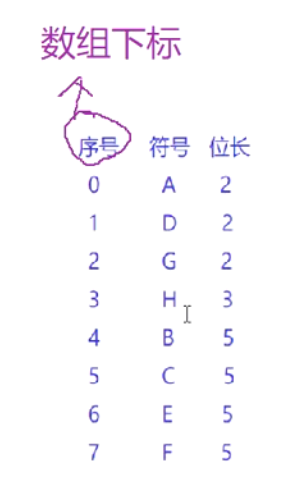
既然范式haffuman树 和 哈夫曼树的编码长度一样,那么压缩比率也将差不多,那么GZIP采用范式哈夫曼树?
1 范范式Huffman树采用静态数组,内部只保存双亲的下标,不用保存孩子下标节省空间。
2 范式哈夫曼树 获取编码效率更快,不用多次递归获取编码
3 关于压缩数据的保存更节省空间。
(只需要保存相应的码字信息(长度))
看下图
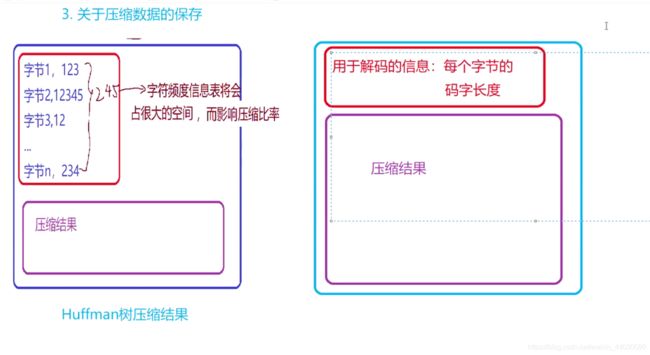
那么每个字节的码字长度(位长)怎么保存?
方式一 :与Huffman 结合:

缺陷 ,字符种类多了,那么需要的空间将很多
2n -1个空间
最坏 255 *2 -1 = 509 字节
方式二:
类似于哈希

没出现的字符为对应为0,出现的字符对应为出现次数,一个字节对应一个字符。
你可能也会想,这样也未必节省空间了吧?弄不好也得255字节呢?
你想的对,真正的GZIP并不是完全的哈希方式保存码字长度(位长)
采用一种游程编码的方式。
思想 ,没出现的一大串0 ,想办法压缩短,就节省了空间。
什么是游程编码?
对于一长串连续出现的数字,只写个字符,紧接着记录出现了多少次。
CL的游程编码 编码的长度即CL也是一对数字,该部分信息理论也可以使用huffman树再次压缩,但是GZIP并没有对其使用
huffman树进行压缩,而是使用了游程编码。 游程,即一段完全相同的数的序列。
**游程编码,即对一段连续相同的数,记录这个数一次,紧接着记录出现
了多少个。**比如CL序列如下:
4, 4, 4, 4, 4, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2 那么,游程编码的结果为:
4, 16, 01(二进制), 3, 3, 3, 6, 16, 11(二进制), 16, 00(二进制), 17,011(二进制), 2, 16, 00(二进 制)
这是什么意思呢?
因为CL的范围是0-15,GZIP认为重复出现2次太短就不用游程编码了,所以游程长度从3开 始。
用16这个特殊的数表示重复出现3、4、5、6个这样一个游程,分别后面跟着00、01、10、11表示
(实 际存储的时候需要低比特优先存储,需要把比特倒序来存,博文的一些例子有时候会忽略这点,实际写程序 的时候一定要注意,否则会得到错误结果)。
于是4,4,4,4,4,这段游程记录为4,16,01,也就是说,4这个数, 后面还会连续出现了4次。6,16,11,16,00表示6后面还连续跟着6个6,再跟着3个6;
因为连续的0出现的可能 很多,所以用17、18这两个特殊的数专门表示0游程,
17后面跟着3个比特分别记录长度为3-10(总共8种可 能)的游程;
18后面跟着7个比特表示11-138(总共128种可能)的游程。
17,011(二进制)表示连续出现6 个0;18,0111110(二进制)表示连续出现62个0。
总之记住
0-15是CL可能出现的值,16表示除了0以外的 其它游程;17、18表示0游程。
因为二进制实际上也是个整数,所以的序列4, 4, 4, 4, 4, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2 用整数表示为:
4, 16, 1, 3, 3, 3, 6, 16, 3, 16, 0, 17, 3, 2, 16, 0
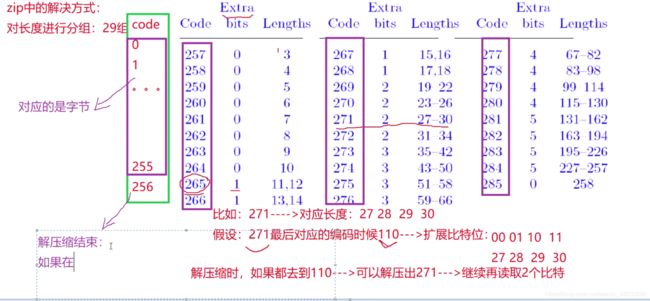
原字符和长度的编码符号总共有286个(256个原字符+1个结束标记+29个长度区间),distance编码区间总共 30个,因此这棵树不会特别深,huffman编码后的码字长度不会特别长,不会超过15,即树的深度不会超过 15,因此CL1和CL2这两个序列的任意整数的值的范围是0-15,0表示没有出现,故GZIP对CL1和CL2使用了游 程编码。
因为游程编码之后整数值的范围是0-18,这个序列称之为SQ,因为码字长度有CL1、CL2,因此最后有SQ1 和SQ2两组数据。GZIP采用第三个huffman树对SQ1和SQ2再次进行huffman压缩。通过统计各个整数(0- 18范围内)的出现次数,按照相同的思路,对SQ1和SQ2进行了Huffman编码,得到的码流记为SQ1 bits和 SQ2 bits。
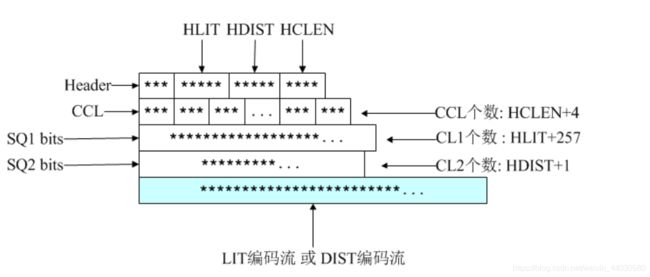
同时,这里又需要记录第三个码表,称为Huffman码表3。同理,这个码表也用相同的方法记录, 也等效为一个码长序列,称为CCL。到此GZIP压缩才算真正结束,这个算法命名为Deflate算法:

Header:3个比特,第一个比特如果是1,表示此部分为最后一个压缩数据块;否则表示这是.ZIP文件的某个 中间压缩数据块,但后面还有其他数据块。这是ZIP中使用分块压缩的标志之一;第2、3比特表示3个选择: 压缩数据中没有使用Huffman、使用静态Huffman、使用动态Huffman,这是对LZ77编码后的 literal/length/distance进行进一步编码的标志。我们前面分析的都是动态Huffman,其实Deflate也支持静 态Huffman编码,静态Huffman编码原理更为简单,无需记录码表(因为PK自己定义了一个固定的码表), 但压缩率不高,所以大多数情况下都是动态Huffman。
HLIT:5比特,记录literal/length码树中码长序列(CL1)个数的一个变量。后面CL1个数等于HLIT+257(因 为至少有0-255总共256个literal,还有一个256表示解码结束,但length的个数不定)。
HDIST:5比特,记录distance码树中码长序列(CL2)个数的一个变量。后面CL2个数等于HDIST+1。哪怕 没有1个重复字符串,distance都为0也是一个CL。
HCLEN:4比特,记录Huffman码表3中码长序列(CCL)个数的一个变量。后面CCL个数等于HCLEN+4。PK 认为CCL个数不会低于4个,即使对于整个文件只有1个字符的情况。
接下来是3比特编码的CCL,一共HCLEN+4个,用以构造Huffman码表3; 接下来是对CL1(码长)序列经过游程编码(SQ1:缩短的整数序列)后,并对SQ1继续用Huffman编码后的
比特流。包含HLIT+257个CL1,其解码码表为Huffman码表3,用以构造Huffman码表1;
接下来是对CL2(码长)序列经过游程编码(SQ2:缩短的整数序列)后,并对SQ2继续用Huffman编码后的 比特流。包含HDIST+1个CL2,其解码码表为Huffman码表3,用于构造Huffman码表2
6. 数据存储格式
因为被压缩的文件可能非常大,会严重影响压缩率,因此GZIP采用了分段压缩处理,每段的压缩结果表示如 下:
标记信息会影响压缩效率, GZIP怎么解决?
2 如果解压缩期间,解除的是256, 代表解压缩结束。
3 如果解压缩的大于256,则表示解压缩出的是长度,再根据Extra扩展,解压出具体长度。
为什么设置为256?
GZIP压缩是分块进行的
如果对整体进行统计时,统计出的字符次数理论上比较均匀,并且字符种类比较多,那么构建的Huffman树节点就比较多,高度也比较大,那么到时候就不好存储,对压缩的比率有很大影响。
因此采用分块压缩
这个图就是Huffman压缩流程原理图。