蓝桥杯省模拟赛

蓝桥杯省模拟赛

后面几题都自己暴力对拍了一下,可能还会有错大家可以参考。

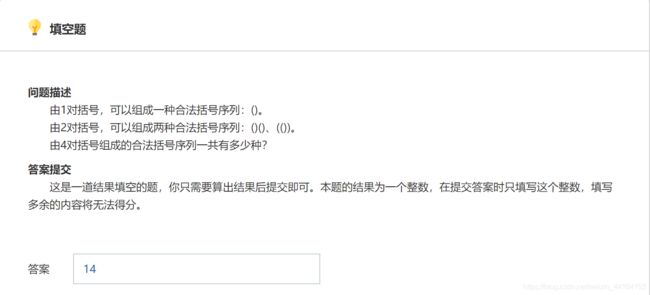
第一题：

基本思路：

我们可以直接手算,或者求稳的话随便枚举一下所有情况就好了,下面是用的状态枚举。
答案： 14

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}

bool can(string s){
	int cnt = 0,n = s.size();
	for(int i = 0 ; i < n ; i++){
		if(s[i] == '(') cnt++;
		else{
			cnt--;
			if(cnt < 0) return false;
		}
	}
	return cnt == 0;
}
signed main() {
  IO;
  int ans = 0;
  for(int i = 0 ; i < (1 << 8) ; i++){
  	string str;
  	int cnt = 0;
  	for(int j = 0 ; j < 8 ; j ++){
  		if(i >> j & 1){
  		 str += '(';
  		 cnt++;
  		}else {
  			str += ')';
  		}
  	}
  	if(cnt != 4) continue;
  	if(can(str)) ans++;
  }
  cout << ans << '\n';
  return 0;
}

第二题：

这个没啥好说的边最少的无向连通图就是树,n-1条边
答案： 2018

第三题：

基本思路：

用全排列函数直接算一下字符串的全排列就好了,可以用set维护一下防止有重复情况。

答案; 2520

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}

signed main() {
	IO;
	string str = "LANQIAO";
	sort(str.begin(),str.end());
	set<string> st;
	do{
		st.insert(str);
	}while (next_permutation(str.begin(),str.end()));
	cout << st.size() << '\n';
	return 0;
}

第四题：

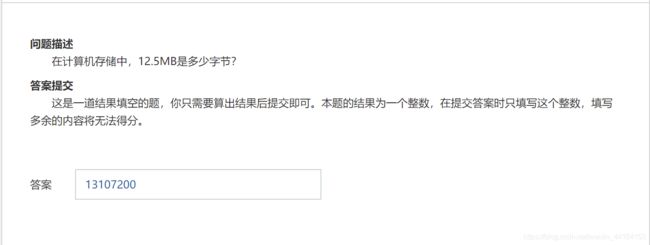
这也没啥好说的,直接手算,或者写个代码打印一下答案就好了。
答案： 13107200

第五题：

基本思路：

很简单，我们先写个26个字母的表,每次算一下原字符字母对应位置往前3个就行了注意是循环数组,模一下26就好了。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}

string ck = "abcdefghijklmnopqrstuvwxyz";
string str;
signed main() {
  IO;
  cin >> str;
  string ans;
  for(int i = 0 ; i < (int)str.size() ; i++){
  	int t = str[i] - 'a';
  	int nt = (t + 3) % 26;
  	ans += ck[nt];
  }
  cout << ans << '\n';
  return 0;
}

第六题：

基本思路：

签到题，随便搞。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}

int n,a,b,c;
int ans = 0;
signed main() {
  IO;
  cin >> n;
  cin >> a >> b >> c;
  rep(i,1,n){
  	if(i % a != 0 && i % b != 0 && i % c != 0) ans++;
  }
  cout << ans << '\n';
  return 0;
}

第七题：

基本思路：

比较麻烦的模拟,先把这个螺旋数组打出来再找就是了,具体模拟过程可以参考代码。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
	int x = 0, neg = 1; char op = getchar();
	while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
	while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
	return neg * x;
}
inline void print(int x) {
	if (x < 0) { putchar('-'); x = -x; }
	if (x >= 10) print(x / 10);
	putchar(x % 10 + '0');
}

const int maxn = 1020;
int n,m;
int res[maxn][maxn];
void solve(){
	int l = 1,t = 1,r = m,k = n;
	int cnt = 0;
	while(true){
		for(int i=l;i<=r;i++){
			res[t][i]=++cnt;
			if(cnt >= n * m) return;
		}
		t++;
		for(int i=t;i<=k;i++){
			res[i][r]=++cnt;
			if(cnt >= n * m) return;
		}
		r--;
		for(int i=r;i>=l;i--){
			res[k][i]=++cnt;
			if(cnt >= n * m) return;
		}
		k--;
		for(int i=k;i>=t;i--){ 
			res[i][l]=++cnt;
			if(cnt >= n * m) return;
		}
		l++;
	}
}
signed main() {
	IO;
	cin >> n >> m;
	solve();
	int r,c;
	cin >> r >> c;
	cout << res[r][c] << '\n';
	return 0;
}

第八题：

基本思路：

这题我们看一下就会发现很像一个dp，但是如果朴素的去dp的话，设dp[i][j]表示在第i个位置,这个位置的数字是j，我们可以得到这样的转移方程即：dp[i][j] = dp[i-1][k](i 是奇数时 j > k , i 是偶数时 j < k) 这样我们需要枚举i,j,k复杂度为O(n^3)肯定过不了100%数据。这时候我们发现k这个部分只有大小关系，所以可以直接用之前答案的前缀和来优化一下,那么优化后复杂度为O(n^2)就能过了。
ps.其实直接开一维dp数组重复使用就是了,不愿改了。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define int long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f
inline int read() {
	int x = 0, neg = 1; char op = getchar();
	while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
	while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
	return neg * x;
}
inline void print(int x) {
	if (x < 0) { putchar('-'); x = -x; }
	if (x >= 10) print(x / 10);
	putchar(x % 10 + '0');
}

const int maxn = 1050;
const int mod = 10000;
int m,n;
int dp[maxn][maxn];
int sum[maxn];
signed main() {
	IO;
	cin >> m >> n;
	for(int i = 1; i <= n; i++){
		dp[1][i] = 1;
	}
	for(int i = 1 ; i <= n; i++){
		sum[i] = (sum[i-1] + dp[1][i]) % mod;
	}
	for(int i = 2 ;i <= m; i++){
		for(int j = 1 ; j <= n; j++){
			if(i & 1){
				dp[i][j] = (dp[i][j] + sum[j-1]) % mod; 
			}else{
				dp[i][j] = (dp[i][j] +  sum[n] - sum[j] + mod) % mod;
			}
		}
		sum[0] = 0;
		for(int j = 1 ; j <= n; j++){
			sum[j] = (sum[j-1] + dp[i][j]) % mod;
		}
	}
	int ans = 0;
	for(int i = 1; i <= n; i++){
		ans += dp[m][i];
		ans %= mod;
	}
	cout << ans << '\n';
	return 0;
}

第九题：

基本思路：

这题看上去复杂其实比较简单,每个村庄之间两两连边然后跑一个MST就行了,这里是用的Kurskal算法,并查集实现。

ps.这题注意一下那个公式里h的位置在外面。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define int long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}

const int maxn = 1010;
int n;
int par[maxn];
void init(){
	rep(i,0,n) par[i] = i;
}
int find(int x){
	return par[x] == x ? x : par[x] = find(par[x]);
}
void unite(int x,int y){
	x = find(x),y = find(y);
	if(x != y) par[x] = y;
}
bool same(int x,int y){
	return find(x) == find(y);
}
struct Edge{
	int u,v;
	double w;
	Edge(int _u,int _v,double _w){
		u = _u,v = _v,w = _w;
	}
	bool operator < (const Edge &e) const{
		return w < e.w;
	}
};
struct Point{
	int x,y,h;
}p[maxn];
double dis(Point a,Point b){
	return sqrt((double)(a.x - b.x) * (a.x - b.x) + (double)(a.y - b.y) * (a.y - b.y)) + (double)(a.h - b.h) * (a.h - b.h);
}
signed main() {
  cin >> n;
  init();
  rep(i,1,n){
  	cin >> p[i].x >> p[i].y >> p[i].h;
  }
  vector<Edge> vec;
  rep(i,1,n){
  	rep(j,1,i-1){
  		double w = dis(p[i],p[j]);
  		vec.push_back(Edge(i,j,w));
  	}
  }
  sort(vec.begin(), vec.end());
  // for(auto it : vec){
  // 	cout << it.u << " " << it.v << " " << it.w << '\n';
  // }
  double ans = 0;
  for(int i = 0 ; i < (int)vec.size() ;i++){
  	int u = vec[i].u,v = vec[i].v;
  	if(!same(u,v)){
  		unite(u,v);
  		ans += vec[i].w;
  	}
  }
  printf("%.2lf\n",ans);
  return 0;
}

第十题：

基本思路：

计算几何+贪心,稍微有些麻烦,我们发现这个n比较小,我们直接贪心一下每次优先取r大的,即先对每个人按照树的半径排个序,然后每次将新树加进来的时候,和已经在答案里的每棵树都比一下看是不是是会相交(这里直接比两圆心距离和两个圆的半径就可以了),不会相交就加入答案,相交就尝试下一个, 基本确定是个假做法,真做法因为范围比较小可能可以暴力dp一下？n <= 20的话枚举状态应该可以搞,但是可能比较麻烦,这里就不写了。

ps.越想越假,别学。

参考代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include 
using namespace std;
#define IO std::ios::sync_with_stdio(false)
#define ll long long
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define per(i, l, r) for (int i = l; i >= r; i--)
#define mset(s, _) memset(s, _, sizeof(s))
#define pb push_back
#define pii pair 
#define mp(a, b) make_pair(a, b)
#define INF 0x3f3f3f3f

inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
inline void print(int x) {
  if (x < 0) { putchar('-'); x = -x; }
  if (x >= 10) print(x / 10);
  putchar(x % 10 + '0');
}
const int maxn = 1010;
struct Point{
	int a,b,c;
	bool operator < (const Point &p) const{
		return c > p.c;
	}
}s[maxn],s2[maxn];
int n,res = 0;
signed main() {
  IO;
  cin >> n;
  rep(i,0,n-1) cin >> s[i].a >> s[i].b >> s[i].c;
  sort(s,s+n);
  int p = 0;
  for(int i = 0 ; i < n; i++){
  	int ok = 1;
  	for(int j = 0 ;j < p ; j++){
  		double d = sqrt((s[i].a-s2[j].a)*(s[i].a-s2[j].a)+(s[i].b-s2[j].b)*(s[i].b-s2[j].b));
  		if(d < (double)(s[i].c + s2[j].c)){
  			ok = 0;
  			break;
  		}
  	}
  	if(ok){
  		s2[p++] = s[i];
  		res += s[i].c * s[i].c;
  	}
  }
  cout << res << '\n';
  return 0;
}