并查集——用于不相交集合的数据结构
并查集
并查集保持一组不相交的动态集合S={S1, S2, ..., SK}。每个集合通过一个代表来表示,代表即集合中的某个成员。
并查集的精髓(即它的三种操作):
集合中的每一个元素是由一个对象表示的,设x表示一个对象。
MAKE-SET(x)
建立一个新的集合,其唯一成员(因而其代表)就是x。因为各个集合是不相交的,故要求x没有在其他集合中出现过。
初始化后每一个元素的父亲节点是它本身,每一个元素的祖先节点也是它本身
示例代码
#include
#include
int father[1001];
int main()
{
int n, m, i, x, y;
while (scanf("%d\n", &n) != EOF && n != 0) {
// 初始化并查集
for (i = 1; i <= n; i ++) {
father[i] = i;
}
}
} UNION(x, y)
将包含x和y的动态集合(比如说Sx和Sy)合并为一个新的集合(即这两个集合的并集).
合并两个不相交集合操作很简单:
利用FIND-SET找到其中两个集合的祖先,将一个集合的祖先指向另一个集合的祖先即可。
示例代码
void union_set(int x, int y)
{
int fx, fy;
if (fx != fy) {
fx = find_set(x);
fy = find_set(y);
}
father[fx] = fy;
}FIND-SET(x)
返回一个指针,指向包含x的(唯一)集合的代表
查找一个元素所在的集合,其精髓是找到这个元素所在集合的祖先!这个才是并查集判断和合并的最终依据。
- 判断两个元素是否属于同一集合,只要看他们所在集合的祖先是否相同即可
- 合并两个集合,也是使一个集合的祖先成为另一个集合的祖先
示例代码
int find_set(int x)
{
while (father[x] != x) {
x = father[x];
}
return x;
}参考题目
题目描述:
Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang's selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.
输入:
The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)
输出:
The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep.
样例输入:
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8
样例输出:
4
2ACCPET代码
#include
#include
int father[10000001];
int number[10000001];
int max;
int find_set(int x);
void union_set(int x, int y);
int main()
{
int i, n, x, y;
while (scanf("%d", &n) != EOF) {
// 初始化集合
for (i = 1; i <= 10000001; i ++) {
father[i] = i;
number[i] = 1;
}
// 合并并查集
max = 1;
for (i = 0; i < n; i ++) {
scanf("%d %d", &x, &y);
union_set(x, y);
}
// 输出结果
printf("%d\n", max);
}
return 0;
}
int find_set(int x)
{
while (x != father[x]) {
x = father[x];
}
return x;
}
void union_set(int x, int y)
{
int fx, fy;
fx = find_set(x);
fy = find_set(y);
if (fx != fy) {
number[fy] += number[fx];
number[fx] = number[fy];
father[fx] = fy;
if (number[fy] > max) {
max = number[fy];
}
}
} 并查集优化
在不相交集合的另一种更快的实现中,用有根树来表示集合,树中的每个结点都包含集合的一个成员,每棵树表示一个集合。通过引入两种启发式策略“按秩合并”和“路径压缩”,就可以获得目前已知的、渐进意义上最快的不相交集合数据结构了
按秩合并
它与我们用于链表的加权合并启发式是相似的。其思想是使包含较少结点的树的根指向包含较多结点的树的根。我们并不显式地记录以每个结点为根的子树的大小,而是采用了一种能够简化分析的方法。对每个结点,用秩表示结点高度的一个上界。在按秩合并中,具有较小秩的根在UNION操作中要指向具有较大秩的根
按秩合并的实现代码:
// 初始化并查集数组
for (i = 1; i <= n; i ++) {
father[i] = i;
rank[i] = 1;
}
paths = (struct path *)malloc(sizeof(struct path) * m);
// 接收边
for (i = 0; i < m; i ++) {
scanf("%d %d %d", &paths[i].u, &paths[i].v, &paths[i].len);
}
qsort(paths, m, sizeof(paths[0]), compare);
// kruskal求最小生成树
for (i = mst = count = 0; i < m; i ++) {
u = find_set(paths[i].u);
v = find_set(paths[i].v);
if (u != v) { // 按秩合并优化
if (rank[u] < rank[v]) {
father[u] = v;
} else {
father[v] = u;
if (rank[u] == rank[v]) {
rank[v] ++;
}
}
mst += paths[i].len;
// 记录次数,判断连通性
count ++;
}
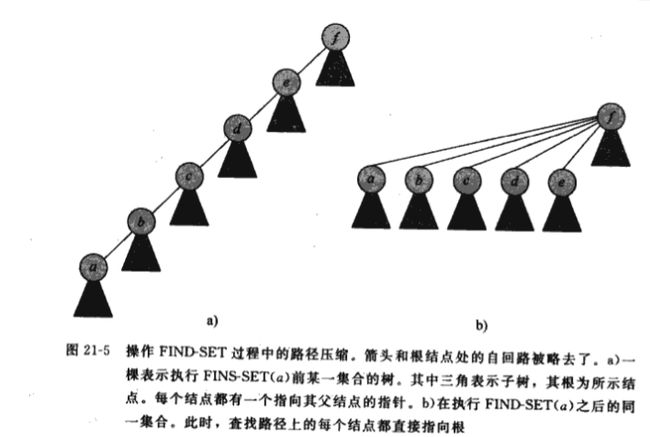
}路径压缩
在FIND-SET操作中,利用这种启发式策略,来使查找路径上的每个结点都直接指向根结点。路径压缩并不改变结点的秩。这个非常简单有效。
带路径压缩的FIND-SET过程也是相当简单的:
int find_set(int x)
{
int parent;
if (x == father[x]) {
return x;
}
parent = find_set(father[x]);
father[x] = parent;
return parent;
}- 第一趟是沿着查找路径上升,直至找到根
- 第二趟是沿查找路径下降,以便更新每个结点,使之直接指向根
图示
示例
这是一个并查集+kruskal算法求最小生成树的题目,在find-set时需要用到“路径压缩”的优化算法,否则会TLE
题目
题目描述:
现在有孤岛n个,孤岛从1开始标序一直到n,有道路m条(道路是双向的,如果有多条道路连通岛屿i,j则选择最短的那条),请你求出能够让所有孤岛都连通的最小道路总长度。
输入:
数据有多组输入。
每组第一行输入n(1<=n<=1000),m(0<=m<=10000)。
接着m行,每行输入一条道路i j d(0<=d<=1000),(i,j表示岛屿序号,d表示道路长度)。
输出:
对每组输入输出一行,如果能连通,输出能连通所有岛屿的最小道路长度,否则请输出字符串"no"。
样例输入:
3 5
1 2 2
1 2 1
2 3 5
1 3 3
3 1 2
4 2
1 2 3
3 4 1
样例输出:
3
noACCEPT代码
#include
#include
struct path
{
int u, v, len;
};
#define MAX 1005
int father[MAX];
int rank[MAX];
int compare(const void *p, const void *q)
{
const struct path *a = p;
const struct path *b = q;
return a->len - b->len;
}
int find_set(int x)
{
int root;
if (x == father[x]) {
return x;
}
root = find_set(father[x]);
father[x] = root;
return root;
}
int main()
{
int i, n, m, u, v, mst, count;
struct path *paths;
while (scanf("%d %d", &n, &m) != EOF) {
// 初始化并查集数组
for (i = 1; i <= n; i ++) {
father[i] = i;
rank[i] = 1;
}
paths = (struct path *)malloc(sizeof(struct path) * m);
// 接收边
for (i = 0; i < m; i ++) {
scanf("%d %d %d", &paths[i].u, &paths[i].v, &paths[i].len);
}
qsort(paths, m, sizeof(paths[0]), compare);
// kruskal求最小生成树
for (i = mst = count = 0; i < m; i ++) {
u = find_set(paths[i].u);
v = find_set(paths[i].v);
if (u != v) {
if (rank[u] < rank[v]) {
father[u] = v;
} else {
father[v] = u;
if (rank[u] == rank[v]) {
rank[v] ++;
}
}
mst += paths[i].len;
// 记录次数,判断连通性
count ++;
}
}
// 打印输出
if (count < n - 1) {
printf("no\n");
}else {
printf("%d\n", mst);
}
free(paths);
}
return 0;
}
/**************************************************************
Problem: 1347
User: wangzhengyi
Language: C
Result: Accepted
Time:920 ms
Memory:1156 kb
****************************************************************/