Python统计学基础

描述性统计

数据类型

数据可分为两类：
1、定性数据：对事物性质进行描述的数据，通常只具有有限个取值，往往用于描述类别
2、定量数据：呈现事物数量特征的数据，是由不同数字组成的，数字取值是可以比较大小的

数据的位置

• 样本平均数 mean()
• 中位数 mdedian()
• 众数 mode() 返回Series类型数据，第二个数是众数
• 百分位数 quantile(i) for i in [0.25,0.75] 返回下四分位数和上四分位数

数据的离散度

• 极差 max()-min()
• 平均绝对偏差 mad()
• 方差 var()
• 标准差 std()

随机变量简介

概率与概率分布

概率（Probability）是用来刻画事物不确定性的一种测度，根据概率的大小，我们可以判断不确定性的高低。概率的取值介于0和1之间，表明一个特定事件以多大的可能性发生。

离散型随机变量

在Python中，通过NumPy包的random模块中的choice()来生成特定的概率质量函数的随机数
choice(a,size=None,replace=True,p=None)

• 参数a：指明随机变量所有可能的取值
• 参数size：表示所要生成的随机数数组的大小
• 参数replace：决定了生成随机数时是否是有放回的
• 参数p：为了一个与x等长的向量，指定了每种结果出现的可能性

RandomNumber = np.random.choice([1,2,3,4,5],size=100,replace=True,p=[0.1,0.1,0.3,0.3,0.2])

连续型随机变量

概率密度函数 和 累计分布函数 都是用来刻画随机变量之不确定性的，描述的是总体的特征。用Python实现
from scipy import stats

• 概率密度函数 gaussian_kde()
• 累计分布函数 cumsum()

期望值与方差

二项分布

Numpy库中
binomial(n,p,size=None)

• 参数n:表示进行伯努利试验的次数
• 参数p：表示伯努利变量取值为1的概率；
• 参数siza：表示生产的随机数的数量
  例子：np.random.binomial(100,0.5,size=20)

正态分布

normal(loc=0.0,scale=1.0,size=None)

• 参数scale:表示正态分布的 标准差，默认为1
• 参数loc：表示正态分布的均值；
• 参数siza：表示生产的随机数的数量
  概率密度值和累计密度值童谣可以使用SciPy的stats模块中函数来计算

#生产5个标准正态分布随机数
Normal = np.random.normal(size=8) 
from scipy import stats
stats.norm.pdf(Normal)#计算随机数的密度
from scipy import stats
stats.norm.cdf(Normal)#计算随机数的累计密度值

其它分布

from scipy import stats

• 卡方分布 stats.chi.pdf()
• t分布 stats.t.pdf()
• F分布 stats.f.pdf()

变量的关系

1、联合概率分布
多个变量之间的联合行为可用联合概率分布。
2、变量的独立性
3、变量的相关性
例如 用corr()函数来描述上证指数和深证指数的收益率的相关性

推断统计

区间估计

Python中stats模块的t类的interval()函数用于在总体方差未知是进行区间估计。
interval(alpha,df,loc,scale)

• alpha 为置信水平
• df是检验的自由度
• loc为样本均值
• scale为标准差

x=[10.3,9.9,11.1,8.9,10.9,12.4,11.3,10.8,8.3,9.5,12.2]
stats.t.interval(0.95,len(x)-1,np.mean(x),stats.sem(x))

假设检验

t检验

单样本t检验

stats.ttest_1samp(样本,均值)

独立样本t检验

判断两个服从正太分布的总体的均值是否存在显著性差异
stats.ttest_ind(样本1,样本2)

配对样本t统计量的构造

当两个样本并不互相独立是，我们可以使用配对样本t检验对两个总体的均值差异进行检验。
stats.ttest_rel(样本1，样本2)

方差分析

方差分析的目的在于分析因子对反应变量有无显著影响，即因子的不同水平下反应变量的均值是否有显著差异。一般分为两大类：
1、 不可控的随机因数
2、研究中施加对结果形成影响的可控因素(因子)

• 离差平方和
• 自由度
  • TSS 衡量的是N个样本的总波动水平，这里所有的N个样本并不独立，它们满足一个约束条件（均值为y）
  • FSS 衡量的是由因子水平变化导致的反应变量取值的波动。但是M个因子组别的均值并不独立
  • ESS 反应的是由于样本与其所处因子水平的组别均值的偏差二产生的波动
• 显著性检验

方差分析之Python实现

导入模型库

import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols

单因素方差分析

model = osl(‘样本某一列 ~ C(样本另一列)’)
table1= anova.anova_lm(model)

model=ols("Return ~ C(Industry)",data=year_return.dropna()).fit()  #建立模型
table=anova.anova_lm(model) #根据模型生成表格
table#不同行业的股票方差

输出结果：

	df	sum_sq	mean_sq	F	PR(>F)
Industry	74.0	60.517228	0.817800	4.177614	4.382045e-28
Residual	2302.0	450.634318	0.195758	NaN	NaN

上述结果，p=4.382045e-28,在0.05的显著水平下，p值远远小于0.05，因此我们可以拒绝原假设（‘Return ~ C(Industry)‘），即（‘A~C (B)‘）不同B的A是不一样的，因此B是影响A的一个重要因素

多因素方差分析

model = osl(‘样本某一列 ~ C(样本另一列)+C(样本另一列)’，data=样本).fit()
table1= anova.anova_lm(model)

析因素方差分析

加号变乘号
model = osl(‘样本某一列 ~ C(样本另一列)*C(样本另一列)’，data=样本).fit()
table1= anova.anova_lm(model)

回归分析

一元线性回归模型

构造上证指数和深圳指数收益率的回归模型

import statsmodel.api as sm
model=sm.OLS(SHRet,sm.add_constant(SZRet)).fit()
print(model.summary())

下表为截距项：

	coef	std err	t	P>|t|	[95.0% Conf. Int.]
const	-0.0003	0.000	-1.747	0.081	-0.001 3.58e-0.5
Retindex	0.7603	0.010	75.487	0.000	0.741 0.780

• R²为0.825，表明模型可以解释上证指数82.5%的方差
• 截距项是-0.0003，p值为0.081>0.05无法通过置信度为0.05的假设检验，可以推断该模型不含截距项，即截距项为0
• 斜率的估值为0.7603，显著不为0（其p值为远远小于0.05的显著水平）
  根据以上结果，可以得出如下模型
  
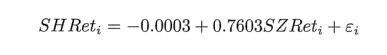
  此外，resid属性为回归的残差项，fittedvalues属性为拟合参数的预测值
  查看前5个拟合值
  model.fittedvalues[:5]

plt.scatter(model.fittedvalues,model.resid)
plt.xlabel("X 拟合值")
plt.ylabel("Y 残差")
plt.legend()

绘制收益率的回归模型

sm.qqplot(model.resid_pearson,stats.norm,line="45")

多元线性回归模型

python代码

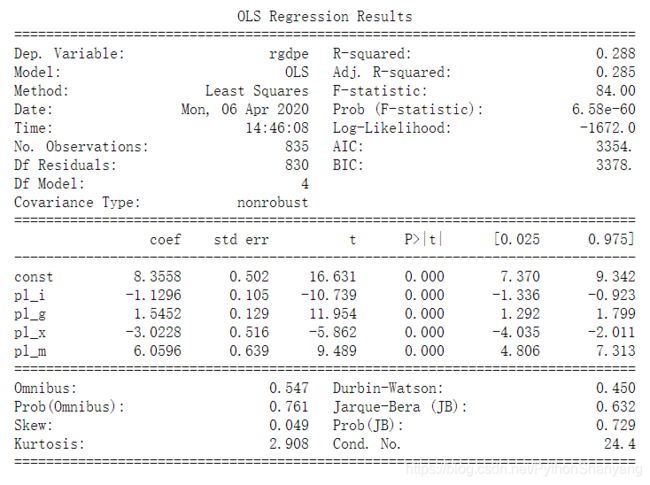
model = sm.OLS(np.log(pen.rgdpe),sm.add_constant(pen.iloc[:,-6:])).fit()
print(model.summary())

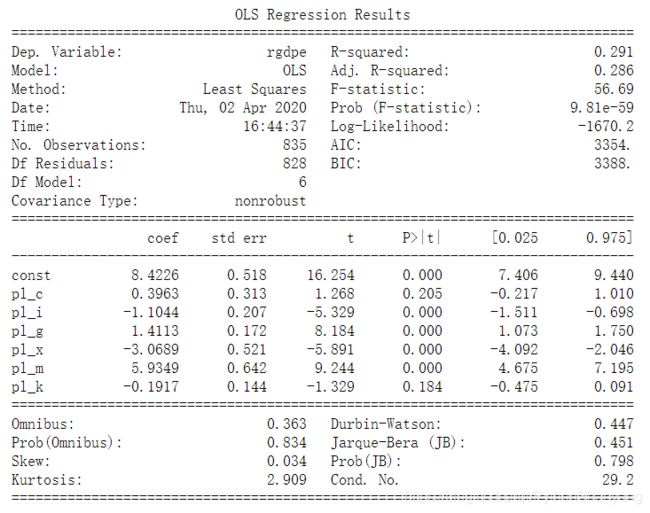
因此，pl_c与pl_k是不显著、pl_i与pl_x与GDP为负相关，pl_g和pl_m则是正相关

考量自变量共线性因素的新模型

剔除pl_c与pl_k

model = sm.OLS(np.log(pen.rgdpe),sm.add_constant(pen.iloc[:,-5:-1])).fit()
print(model.summary())

本文章引用：《量化投资以Python为工具》