Summary of Effective Recommendation Algorithms

简介

本文以问题为导向介绍推荐算法。

问题一

问题定义：假设$U=\{u_1,u_2,...,u_n\}$表示用户集合， $P=\{p_1,p_2,...,p_m\}$表示物品集合，$S\in R^{n\times m}$表示用户对物品的评分组成的矩阵，例如$s_{ij}$表示用户$u_i$对物品$p_j$的评分，如果用户$u_i$没有对物品$p_j$没有评过分数，则对应的矩阵项为空。我们的目标是为用户生成个性化的TopN推荐列表。

1. 基于用户的协同过滤

按照基于用户的协同过滤算法，我们需要找到目标用户的相似用户，首先可以用用户各自的评分组成的向量表示用户，比如要计算两个用户的$u_a,u_b$的相似度，则$u_a=[s_{a1},s_{a2},...,s_{am}],u_b=[s_{b1},s_{b2},...,s_{bm}]$,然后计算用户向量间的相似度。向量相似度的计算方式有很多，比如欧式距离、协方差、余弦相似、Pearson相关系数、Jaccard系数等。

• 欧式距离的计算公式为：

$$d(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

欧式距离的取值范围是0到正无穷，取值越小表示相似度越高，取值为零表示两个向量完全相等。

• 协方差的计算公式为：
  $$Con(x,y)=E[(x-E[x])(y-E[y])]=E[xy]-E[x]E[y]$$

• Pearson相似度的计算公式为:

$$\rho (x,y)=\frac{Con(x,y)}{{\sigma }_x{\sigma }_y}=\frac{E[x-E[x]])(y-E[y]}{{\sigma }_x{\sigma }_y}$$

其中${\sigma }_x,{\sigma }_y$分别表示x,y的标准差。

• 余弦相似度计算公式：

$$cos(x,y)=\frac{\sum x_i{y}_i}{|x||y|}=\frac{\sum x_i{y}_i}{\sqrt{{\sum }_i{x}_i^2}\sqrt{{\sum }_i{y}_i^2}}$$

那么如何选择相似度的计算方法呢？这些相似度计算方法之间满足下面的关系

定理一：数据标准化之后（均值为0，标准差为1），Pearson相关系数等于余弦相似度

证明如下：

$$\rho (x,y)=\frac{Con(x,y)}{{\sigma }_x{\sigma }_y}$$
$$=\frac{E[(x-E[x]])(y-E(y))}{{\sigma }_x{\sigma }_y}$$

$E[x]=0,E[y]=0,{\sigma }_x=1,{\sigma }_y=1$带入以上公式得到;

$$\rho (x,y)=E(xy)=\frac{{\sum }_i{x}_i{y}_i}{N}$$

又因为：

$$cos(x,y)=\frac{{\sum }_i{x}_i{y}_i}{\sqrt{{\sum }_i{x}_i^2}\sqrt{{\sum }_i{y}_i^2}}$$
$$=\frac{{\sum }_i{x}_i{y}_i}{N\ast \sqrt{{\sum }_i{x}_i^2/N}\sqrt{{\sum }_i{y}_i^2/N}}$$
$$=\frac{{\sum }_i{x}_i{y}_i}{N}$$
$$=\rho (x,y)$$

定理二：数据标准化之后（均值为0，标准差为1），Pearson相关系数有欧式距离的平方满足线性关系

证明如下：

$$d(x,y{)}^2=\sum _i^n(x_i-y_i{)}^2$$
$$=\sum _i^n(x_i^2-2x_i{y}_i+y_i^2)$$
$$=\sum _i^n{x}_i^2+\sum _i^n{y}_i^2-2\sum _i^n{x}_i{y}_i$$
$$=n\sum _i^n\frac{x_i^2}{n}+n\sum _i^n\frac{y_i^2}{n}-2\sum _i^n{x}_i{y}_i$$
$$=n{\sigma }_x^2+n{\sigma }_y^2-2\sum _i^n{x}_i{y}_i$$
$$=n+n-2n\rho (x,y)$$
$$=2n(1-\rho (x,y))$$

定理三：数据标准化之后（均值为0，标准差为1），预选相似度与欧式距离平方满足线性关系

回到推荐算法，我们以Pearson相似度计算为例，用户$u_a,u_b$之间的相似度计算公式为;

$$sim(a,b)=\frac{{\sum }_{i\in P(a,b)}(s_{ai}-{\mu }_a)(s_{bi}-{\mu }_b)}{\sqrt{{\sum }_{i\in P(a,b)}(s_{ai}-{\mu }_a{)}^2}\sqrt{{\sum }_{i\in P(a,b)}(s_{bi}-{\mu }_b{)}^2}}$$

其中$P(a,b)$表示a,b用户共同评过分的物品集合，${\mu }_a,{\mu }_b$分为表示用户a，b评分的均值。

有了用户相似度计算方法之后，就可以利用相似用户的评分，预测目标用户的评分，比如a用户对物品p的评分可以通过下面公式预测：

$$Pred(a,p)={\mu }_a+\frac{{\sum }_{b\in U(a,K)}sim(a,b)(s_{bp}-{\mu }_b)}{{\sum }_{b\in U(a,K)}sim(a,b)}$$

其中$U(a,K)$表示与用户相似度最高的TopK个用户组成的集合。

以上是最基本的基于相似用户的推荐算法，实践中可以有几个方向的改进：

• 在计算用户相似度的时候，并没有考虑热门物品的影响，显然喜爱这类热门物品，并不表示两位用户的兴趣比较相似，相反，共同喜爱某些冷门物品，更能表示两个用户的兴趣比较类似。
• 在计算用户相似度的时候，并没有考虑用户有多少个共同评分的物品。显然当用户虽然评分非常一致，但是只对极少数物品评分，也并不能表示两位用户的兴趣类似。

改进算法就不在这里展开了，可以通过设计一些加权算法赋予不同的物品以不同的权重来改进基本版本的算法。

2. 基于物品的协同过滤

类似的，有了评分矩阵后，物品a,b的评分表示为$p_a=[s_{1a},s_{2a},...,s_{na}],p_b=[s_{1b},s_{2b},...,s_{nb}]$。我们可以直接通过相似度计算方法计算两个物品的相似度,比如余弦相似度为:

$$sim(a,b)=\frac{{\sum }_{i\in U(a,b)}{s}_{ia}{s}_{ib}}{\sqrt{{\sum }_{i\in U(a,b)}{s}_{ia}^2}\sqrt{{\sum }_{i\in U(a,b)}{s}_{ib}^2}}$$

其中$U(a,b)$表示对物品a,b都评过分的用户的集合。

有了物品的相似度后，可以预测某个用户对某个物品的评分值：

$$Pred(u,p)=\frac{{\sum }_{i\in P(u,p)}sim(i,p)s_{ui}}{sim(i,p)}$$

其中$P(u,p)$表示用户u评过分的与物品p相似的物品集合。

以上的相似度计算方法，在实践中与几个方向的改进：

• 在计算物品相似度的时候，各个纬度是同等加权的，实际中不同用户对物品相似度的贡献不一样的。活跃用的兴趣可能比较宽泛，这类用户喜欢物品，并不能说明两类物品比较类似。
• 在计算物品相似度的时候，并没有考虑共同评分的用户数量。显然被极少数用户评论过并不能代表物品比较相似。

3. 基于奇异值分解(SVD)

奇异值分解的原理是将原始的评分矩阵分解为3个矩阵乘积的形式：

$$S=U\Sigma V^T$$

其中$U,V$称为左右奇异向量，$\Sigma$对角线墒的值称为奇异值。

分解矩阵之后，如何对目标用户进行推荐呢？

拿到目标用户的评分向量$u_v$，首先计算目标用户在低位空间的位置:

$$u_v^{\prime }=u_{v}U{\Sigma }^{-1}$$

有了目标用户子低维空间的位置，可以有不同的策略为她推荐物品，比如可以在低维空间寻找相似用户，用相似用户的物品评分预测目标用户的物品评分。

对以上的基本算法可以有几个方向的改进：

• 加权方案
• 缺失评分的填充方案

4. 基于隐语义学习(LFM)

首先基础的LFM通过下面的公式计算用户对物品的评分：

$$s_{ui}=p_u{q}_i^T=\sum _{k=1}^K{p}_{u,k}{q}_{i,k}$$

其中$p_{u,k},q_{i,k}$称为模型的参数。那么如何得到模型的参数呢？可以通过最小化下面的损失函数来计算模型的参数：

$$C=\sum (s_{ui}-s_{ui}{)}^2$$

一般为了防止过拟合，我们会在损失函数上加上正则化：

$$C=\sum ((s_{ui}-s_{ui}{)}^2+\lambda |p_u{|}^2+\lambda |q_i{|}^2)$$

关于机器学习的内容我们在其他文章里有详细的介绍，这里就不展开了。

我们来对基础的LFM做一些改进：

• 我们将系统的偏移信息用独立的模型参数来表示：

$$s_{ui}=p_u{q}_i^T+b_u+b_i+\mu$$

其中$b_u,b_i,\mu$分别表示用户评分的偏置，物品评分的偏执，全局平均分。

如此则损失函数变成：

$$C=\sum ((p_u{q}_i^T+b_u+b_i+\mu -s_{ui}{)}^2+\lambda (|p_u{|}^2+|q_i{|}^2+|b_u{|}^2+|b_i{|}^2))$$

• 我们将用户的属性加入到模型，比如用户的年龄、地域等，每一个属性值都对应一个隐因子

$$s_{ui}=(p_u+\sum a_u)q_i^T+b_u+b_i+\mu$$

• 我们将用户的消费过的物品加入模型，每个消费过的物品都对应一个隐因子

$$s_{ui}=(p_u+\sum a_u+|N(u{)}^{-0.5}|\sum _{k\in N(u)}{y}_k)q_i^T+b_u+b_i+\mu$$

• 加入时间的考虑，或对样本进行时间的加权，或将重要的时间特征对应隐因子加入模型，或将样本按时间分类，不同时间段对应不同的参数。

有了这些隐因子之后，如何对目标用户进行推荐呢？很简单，有了隐因子之后，我们可以直接估算用户对某个物品的评分了，按评分的高低生成TopN推荐列表。

问题二

问题定义：假设$U=\{u_1,u_2,...,u_n\}$表示用户的集合，$P=\{p_1,p_2,...,p_m\}$表示物品的集合，$P(u_i)，u_i\in U$表示用户i的所以有正反馈的物品组成的集合。这里的正反馈可以是隐式反馈。目标是为用户生成TopN推荐列表。

1. 基于用户协同过滤

Jaccard相似度计算：

$$sim(u,v)=J(u,v)=\frac{|P(u_u)\cap P(u_v)|}{|P(u_u)\cup P(u_v)|}$$

余弦相似度计算：

$$sim(u,v)=Cos(u,v)=\frac{|P(u_u)\cap P(u_v)|}{\sqrt{|P(u_u)|}\sqrt{|P(u_v)|}}$$

有了相似用户之后，就可以预测目标用户对目标物品的兴趣程度：

$$Pred(u,p)=\frac{{\sum }_{v\in U(u,K)\cap U(p)}sim(u,v)r_{vp}}{{\sum }_{v\in U(u,K)\cap U(p)}sim(u,v)}$$

其中$U(u,k)$表示与用户u最相似的K个用户组成的集合，$U(p)$表示对物品p有个正反馈的用户集合。

我们对以上的基本算法做一下改进：

• 我们在计算用户相似度的时候，没有考虑热门物品的影响，热门和非热门物品度对用户相似度的影响程度一样。显然这事不太对的，因为共同喜欢热门物品，并不能表示两个用户的兴趣比较类似，只能说明这个物品比较热门，被大多数人喜欢。

所以我们改进用户相似度的计算方法：

$$sim(u,v)=ImprovedCos(u,v)$$
$$=\frac{{\sum }_{p\in P(u_u,u_v)}\frac{1}{log(1+|U(p)|)}}{\sqrt{|P(u_u)|}\sqrt{|P(u_v)|}}$$

其中$U(p)$表示对物品p有过正反馈的用户集合。

2. 基于物品协同过滤

物品的余弦相似度计算法公式为：

$$sim(i,j)=\frac{|U(i)\cap U(j)|}{\sqrt{|U(i)|}\sqrt{|U(j)|}}$$

有了物品相似度之后可以预测用户对物品的兴趣程度：

$$Pred(u,p)=\frac{{\sum }_{i\in P(p,K)\cap P(u)}sim(p,i)r_{ui}}{{\sum }_{i\in P(p,K)\cap P(u)}sim(p,i)}$$

其中$P(p,K)$表示物品p最相似的K个物品的集合，$P(u)$表示用户u正反馈过的物品集合。

下面我们对上面的基本算法做个改进：

• 在上面计算物品相似度的时候，所有用户对物品相似度的贡献值是一样的。这个假设不太合理，活跃用户对相似度的影响应该小于非活跃用户，这个概念被称为反用户频率(Inverse Uesr Frequence)。因为被活跃用户感兴趣的物品，不一定很相似。

改进后的相似度计算方式为：

$$sim(i,j)=ImprovedCos(i,j)=\frac{{\sum }_{u\in U(i)\cap U(j)}\frac{1}{log(1+|P(u)|)}}{\sqrt{|U(i)|}\sqrt{|U(j)|}}$$

3. LFM模型

LFM模型在评分预测类的任务中表现很好，同样在行为预测类的任务中也可以使用:

$$s_{ui}=(p_u+\sum a_u+|N(u{)}^{-0.5}|\sum _{k\in N(u)}{y}_k)q_i^T+b_u+b_i+\mu$$

正样本总取$s_{ui}=1$,负样本则取$s_{ui}=0$. 在这类任务中，训练数据只有正样本，而没有负样本。所以首先需要解决的问题是如何为用户生成负样本数据。

负样本的采样策略可以是简单的，随机的从用户没有过行为的数据中选取。但是也有一些改进的方法，比如偏重热门物品，因为热门的物品用户大概率看到过，但是没有正反馈，这表示是一个负样本。

4. 基于图的算法

基于图的推荐算法中，我们首先需要将用户的行为数据表示成图的形式。

定义：我们将用户的行为表示为图$G=(V_u,V_I,E)$，其中$V_u$表示用户顶点集合，每一个顶点表示一个用户，$V_I$表示物品顶点集合，每一个顶点表示一个物品。用户的历史行为可以表示为[用户，物品]二元组的形式，对于每一个这样的二元组，图G中都存在一条连接对应用户和物品的边，构成集合$E$.

例如有用户$u_1,u_2,u_3,u_4$,分别有各自的历史行为，他们的历史行为表示为图的形式如下：

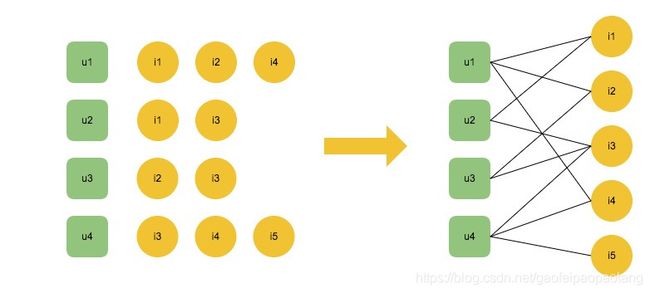
用户的行为表示为图的形式之后，推荐过程就是在图中寻找与目标用户顶点具有相关性的物品顶点。那么首先需要解决的是如何衡量图中顶点间的相关性。

实践中研究人员设计了很多计算图中顶点相关性的算法。这里介绍一种基于随机游走的PersonalRank算法。对于每一个目标用户$v_u$，我们通过下面的公式计算顶点的权重：

$$Rank(v)=\alpha \sum _{v^{\prime }\in in(v)}\frac{Rank(v^{\prime })}{|out(v)|}if(v\ne v_u)$$

$$Rank(v)=(1-\alpha )+\alpha \sum _{v^{\prime }\in in(v)}\frac{Rank(v^{\prime })}{out(v)}if(v=v_u)$$

经过若干次的迭代后顶点的权重会收敛，此时的权重值可以作为物品推荐的分数。

5. 基于内容的算法

基于内容的推荐算法的基本思想是给目标用户推荐他喜欢的物品的相似物品，但与基于物品的协同的过滤算法不同，物品间的相似度由物品的属性（物品类别、标签等等）决定，而不是由物品上积累的用户行为决定。由于不需要物品上积累的用户行为，基于内容的推荐算法在物品冷启动阶段非常有用。

基于内容的推荐可以分成三个阶段：

• 物品的分析阶段，生成物品画像，包括物品的类别、标签、价格、品牌等等。物品画像的维度同时也定义了用户画像的维度。
• 用户兴趣点提取阶段，生成用户兴趣点画像
• 根据用户的兴趣点生成推荐列表

第一阶段我在其他的文章中有详细介绍过，涉及的算法根据物品的不同，可能会涉及文本处理、图像处理、人工生成标签等等，这里不展开，重点介绍一下二三阶段。

首先遇到的问题是什么是兴趣点？前面已经提到了，物品画像的维度定义了用户的兴趣点。

第二个问题是如何提取用户的兴趣点？基本是方式是通过用户与物品的交互行为历史(浏览、点击、收藏、购买、分享、屏蔽等)生成用户的兴趣点。

一般来说，兴趣点的提取可以从考虑以下的量化指标：

• 兴趣点的正向反馈绝对次数
• 兴趣点的正向反馈比率

我们来对兴趣点的提取做一些改进：

• 上面在提取兴趣点的时候，没有考虑兴趣点本身的热门程度，我们加入反兴趣点自身频率的考虑，因为这样才会捕捉到用户的非热门的兴趣点。
• 加入时间衰减的考虑，最近的正向反馈行为的权重要大于一段时间前的正向反馈行为
• 分时间段的兴趣点提取

在第三个阶段，有了用户的兴趣点之后，如何为用户生成推荐内容呢？这里可以有不同的推荐策略，比如简单的可以将兴趣点作为检索关键词直接检索出相关的物品。也可以加入一些实时兴趣点筛选逻辑，根据用户当时的状态实时决定用哪些兴趣点。

6. 排行榜推荐策略

排行榜可能是最容易被忽视的非个性化的推荐策略，但在很多情况下不失为一种很好的推荐策略。

常见的排行榜有：

• 物品点击排行榜
• 物品时效性排行榜

我们在基本的排行榜策略里，加入用户的人口统计学特征，比如性别、年龄、 地域、职业等特征，可以生成半个性化的排行榜。

7. 社会化推荐

社会化推荐是指利用用户的社交关系进行推荐的策略。有了用户的社交关系，最简单的推荐策略就是给目标用户推荐其好友喜欢的物品集合：

$$s_{ui}=\sum _{v\in Related(u)}{w}_{uv}{s}_{vi}$$

其中$Related(u)$表示用户u的好友集合。$s_{v}i$表示用户v对物品i的兴趣程度。$w_{uv}$表示用户u,v间的熟悉程度的权重。

还有一些社会化推荐算法，将用户间的好友关系以及用户与物品间的兴趣关系通过图的形式表示，然后采用基于图的推荐算法。

8. 深度学习的实践

深度学习在建模和表示用户的兴趣上有很多卓有成效的实践。大规模的推荐系统中，推荐过程一般分为两个阶段：召回阶段和排序阶段。召回阶段负责从海量的物品集合中选择并生成一个推荐物品候选集合，候选集合规模相对较小；排序阶段负责基于一定的目标（点击、消费等等，或则是多目标）对候选集合内的物品进行排序，并生成最终的推荐列表。深度学习在两个阶段都有应用。

召回阶段：

• 基于Embedding思想的用户兴趣建模算法，比如以前文章中介绍过的Graph Embedding, MIND

排序阶段;

• WideAndDeep, 多目标模型，ESMM

9. 其他推荐算法

还有一些推荐算法，感兴趣的可以搜索相关的paper阅读了解，以后有时间在做详细展开：

• 基于受限玻尔兹曼机的推荐算法
• 基于增强学习的推荐算法

问题三

问题定义：假设待推荐的物品集合为$P=\{p_1,p_2,...,p_n\}$，用户的整体集合为$U=\{u_1,u_2,...,u_m\}$。 我们的目标是为每个待推荐的物品$p_i\in P$生成一个用户列表，将物品推送给用户。

这是一个典型的推送问题，属于推荐问题范畴，但与通常的推荐问题不同点在于：

• 通常的推荐问题是为用户找到合适的物品，而推送问题是为物品找到合适的用户

以上的算法进过简单的变化即可以用在推送问题上，这里不再展开。

从实现层面来说，推送系统的结构与通常的推荐系统的结构比较相似，通常分为两个阶段：召回阶段和排序阶段。召回阶段负责从海量的用户集合中挑选可能对物品感兴趣的用户并生成备选用户候选集合。排序阶段负责以特定指标为目标（点击、消费、够买等）对候选集中的用户进行排序。