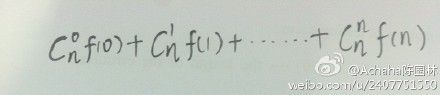矩阵快速幂专题【完结】

第一题 hdu 1757 A Simple Math Problem

点击打开链接

思路：矩阵快速幂

分析:

1 最简单的矩阵快速幂的题目，直接利用矩阵求解即可

点击打开查看代码

第二题 hdu 1575Tr A

点击打开hdu 1575

思路: 矩阵快速幂

分析:

1 题目给定一个n*n的矩阵要求矩阵的k次幂之后的矩阵的对角线的和

2 矩阵快速幂的裸题

点击打开查看代码

第三题 hdu 2604 Queuing

点击打开hdu 2604

思路: 递推+矩阵快速幂

分析;

1 根据题目的意思，我们可以求出F[0] = 0 , F[1] = 2 , F[2] = 4 , F[3] = 6 , F[4] = 9 , F[5] = 15

2 那么根据上面前5项我们可以求出n >= 5的时候 F[n] = F[n-1]+F[n-3]+F[n-4]

那么我们就可以构造出矩阵

| 1 0 1 1 | | F[n-1] | | F[n] |

| 1 0 0 0 | * | F[n-2] | = | F[n-1] |

| 0 1 0 0 | | F[n-3] | | F[n-2] |

| 0 0 1 0 | | F[n-4] | | F[n-3] |

点击打开查看代码

第四题 hdu 2256Problem of Precision

点击打开hdu 2256

思路: 矩阵快速幂

分析:

1 题目要求的是(sqrt(2)+sqrt(3))^2n %1024向下取整的值

3 这里很多人会直接认为结果等于(an+bn*sqrt(6))%1024，但是这种结果是错的，因为这边涉及到了double，必然会有误差，所以根double有关的取模都是错误的思路

点击打开查看代码

第五题 codeforces 185APlant

点击打开cf 185A

思路: 递推+矩阵快速幂

分析:

1 题目要求找到在n年后向上三角形的个数

2 写出前面的几个数F(0) = 1 , F(1) = 3 , F(2) = 10 , F(3) = 36 , F(4) = 136

通过前面几项我们可以找到通项公式F[n] = 4*F[n-1]-2^(n-1)

那么我们通过够找矩阵

| 4 -1 | * | F(n-1) | = | F(n) |

| 0 2 | | 2^(n-1) | | 2^n |

3 那么够造出矩阵之后我们直接利用矩阵快速幂，由于矩阵开始有负数，所以应该在取模的时候注意一下

点击打开查看代码

第六题 hdu 2842Chinese Rings

点击打开hdu2842

思路: 矩阵快速幂

分析:

1 题目的意思是给定n个环，和一些规则要把所有的环全部拆下最少需要的步数

2 题目规定如果要拆第n个环，那么第n-1个要挂着，n-2环要被拆下。那么我们设f(n)表示拆下前n个环的最少的步骤

那么考虑第n个环的情况，第n-1个环必须要挂着，n-2环要拆下，那么这一步就要f(n-2)，拆下第n个需要1步。然后只剩下第n-1个环，由于n-1环需要第n-2环挂着，所以我们需要把前n-2个环挂上去，所以需要f(n-2)，剩下n-1个需要拆下需要f(n-1)。那么总的需要f(n) = f(n-2)+1+f(n-2)+f(n-1) => f(n) = 2*f(n)+f(n-1)+1

3 接下来利用矩阵快速幂即可

点击打开查看代码

第七题 hdu 2276Kiki & Little Kiki 2

点击打开hdu 2276

思路: 矩阵快速幂

分析:

1 题目给定一个01字符串然后进行m次的变换，变换的规则是：如果当前位置i的左边是1（题目说了是个圆，下标为0的左边是n-1），那么i就要改变状态0->1 , 1->0

比如当前的状态为100101那么一秒过后的状态为010111

2 假设0/1串的长度为n，保存在a数组，下标从0开始

根据上面的规则我们发现可以得出一秒过后的状态即为a[i] = (a[i]+a[i-1])%2 , 对于a[0] = (a[0]+a[n-1])%2

那么我们就可以就能够找到递推的式子

1 1 0 0.... a0 a1

0 1 1 0... * a1 = a2

..........1 1 ..... .....

1 0 0.....1 an-1 a0

3 但是我们最后要求的是a0 a1 .... an-1 ， 所以我们应该把矩阵的第一行和最和一行调换一下，然后进行m次的快速幂即可

4 由于最后的结果是mod2的结果，因此我们可以把所有的*和+运算全部改成&和^

5 由于初始的矩阵是一个循环同构的矩阵，因此我们可以每次先求出第一行，然后在递推出第二行，那么这样就从O(n^3)降到O(n^2)

点击打开查看代码

第八题 hdu 2254 奥运

点击打开hdu 2254

思路: 矩阵乘法

分析:

1 题目给定一个有向图，要求t1-t2天内v1-v2的路径的个数

2 假设有向图的邻接矩阵为A，那么A表示的是有向图中走一步能够到达哪些点的方案数，那么A^n表示的是走n步能够到达哪些点的方案数

3 根据离散数学里面的可达矩阵的性质，我们知道一个有向图的邻接矩阵的前n次幂的和即为可达矩阵，那么要求[t1-t2]之内的路径的条数，因为题目说了t1 = 0的时候为0。那么假设邻接矩阵为A，那么要求的就是A^(t1-1)+A^(t1)+...+A^(t2-1)，为什么是从t1-1开始呢，因为邻接矩阵本身代表走一步的结果

3 还有点的范围很大，边数很少，所以我们应该要进行离散化

4 但是数据量很大，对于具体的一组我们应该要事先求出具体的每一个矩阵，然后直接使用即可

点击查看代码

第九题 hdu 3117Fibonacci Numbers

点击打开hdu 3117

思路: 矩阵快速幂

分析:

1 题目要求的是求F(n)中如果位数的个数大于8那么要输出前4四位和后四位，没有到8位的时候直接输出

2 根据题目的样例我们可以知道当n = 40的时候就超过8位了，所以我们可以知道n <= 39的时候直接去求F(n)，超过40的时候我们就要去求前4位和后四位

3 我们利用矩阵快速幂可以很快的求出后四位，但是前面四位就很困难了

下面看一下网上的解法：转载自点击打开链接

点击查看代码

第十题 hdu 4686 Arc of Dream

点击打开hdu 4686

思路: 矩阵快速幂

分析:

1 题目给定一个式子求和，那么根据题目给定的，我们可以求出an*bn = (an-1*Ax+Ay)*(bn-1*Bx+By) => an-1*bn-1*Ax*Bx+an-1*Ax*By+bn-1*Ay*Bx+Ay*By

2 那么我们根据上面的等式可以推出矩阵的乘法

3 那么我们要求的是AoD(n)相当于求左边矩阵的n次幂，然后利用结果乘上初始值

4 注意特判n为0的时候，结果为0。然后注意初始的值

点击查看代码

第十一题 zoj 3690 Choosing number

点击打开zoj 3690

思路: 递推+矩阵快速幂

分析;

1 题目的意思是有n个人和m个数和一个k，现在每个人可以选择一个数，但是要求如果相邻的两个人选择相同的数，那么这个数要大于k

2 假设F(n)表示前n个人第n个人选择的数大于k的个数，G(n)表示的是前n个人第n个人选择的数小于等于k的个数

那么F(n) = F(n-1)*(m-k)+G(n-1)*(m-k) , G(n) = F(n-1)*k+G(n-1)*(k-1) , 那么最后的结果就是F(n)+G(n);

那么我们可以构造出矩阵

| m-k m-k| | F(n-1) | | F(n) |

| k k-1| * | G(n-1) | => | G(n) |

那么初始值F(1) = m-k , G(1) = k

点击查看代码

第十二题 FZU 1683 纪念SlingShot

点击打开FZU1683

思路: 矩阵快速幂

分析:

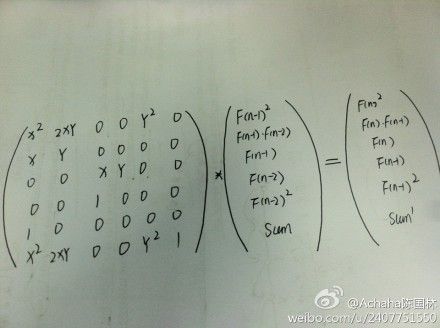
1 题目给定f(n) = 3*f(n-1)+2*f(n-2)+7*f(n-3) , f(0) = 1 , f(1) = 3 , f(2) = 5 ，给定n求f(0)+...+f(n) %2009

2 矩阵快速幂的水题，我们构造出这样的矩阵，然后利用矩阵快速幂即可

3 2 7 0 f(n-1) f(n)

1 0 0 0 * f(n-2) = f(n-1)

0 1 0 0 f(n-3) f(n-2)

3 2 7 1 sum sum'

点击查看代码

第十三题 hdu 3306 Another kind of Fibonacci

点击打开hdu 3306

思路: 矩阵快速幂

分析:

1 题目给定另外一种递推式，A(0) = 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2).求 S(N) , S(N) = A(0)² +A(1)²+……+A(n)²

2 那么我们通过这个式子就可以构造出以下的矩阵

点击查看代码

第十四题 UESTC 1335 Fibonacci

点击打开UESTC 1335

思路: 矩阵快速幂

分析:

1 最简单的矩阵快速幂

点击查看代码

第十五题 poj 3233 Matrix Power Series

点击打开poj 3233

思路: 二分求和+矩阵快速幂

分析:

1 题目给定一个n*n的矩阵A，要求(A+A^2+....A^K)%m后的矩阵

2 对于任意的A^x，我们都能够利用矩阵快速幂求出，但是我们现在要求的是和。

仔细观察整个式子，那么我们可以对原式进行变形

如果k为偶数，那么(A+A^2+....A^K) = (A+...+A^K/2)+A^K/2*(A+...+A^K/2)

如果k为奇数，那么(A+A^2+....A^K) = (A+...+A^K/2)+A^K/2*(A+...+A^K/2)+A^k

3 那么对于上面的式子的变形，就是二分的思想，那么我们可以利用二分来求和，然后对于单个的矩阵的x次方我们利用快速幂

点击查看代码

第十六题 hdu 4565 So Easy!

点击打开hdu 4565

思路: 递推+矩阵快速幂

分析:

1 这一题和hdu 2256

几乎就是一模一样的题目，只是这边要求的是向上取整

那么我们按照hdu2256的思路来做即可点击打开hdu 2256

点击查看代码

第十七题 uva 10870 Recurrences

点击打开uva 10870

思路:构造矩阵+矩阵快速幂

分析:

1 题目给定f(n)的表达式 f(n) = a₁ f(n - 1) + a₂ f(n - 2) + a₃ f(n -3) + ... + a_d f(n - d)对于n > d的时候

2 那么我们可以构造出矩阵

a1 a2 ... an f(n-1) f(n)

1 0 ......... 0 f(n-2) f(n-1)

0 1 ..........0 * ........ => ......

.................. ....... ......

0 0 ...... 1 0 ....... f(n-d)

0 0 0 0 ... 0 f(n-d) f(n-d+1)

3 题目有个地方错了，两个case之间根本不需要空行

点击查看代码

第十八题 light oj 1132 Summing up Powers

点击打开light oj 1132

思路: 构造矩阵+矩阵快速幂

分析:

1 题目给定n和k要求(1^K + 2^K + 3^K+ ... + N^K) % 2³²

2 具体的思路见下图

3 对于求组合数，我们可以利用公式C(n , k+1) = C(n , k)*(n-k)/(k+1) ，那么我们可以先打表求出50之内的所有的组合数

点击查看代码

第十九题 FZU 1692 Key problem

点击打开FZU 1692

思路: 构造矩阵+矩阵快速幂

分析:

1 题目的意思是有n个人构成一个圈，每个人初始的有ai个苹果，现在做m次的游戏，每一次游戏过后第i个人能够增加R*A_(i+n-1)%n+L*A_{(i+1)%n 个苹果（题目有错），问m轮游戏过后每个人的苹果数}

_{2 根据题目的意思我们能够列出一轮过后每个人的苹果数}

_{a0 = a0+R*an-1+L*a1}

_{a1 = a1+R*a0+L*a2}

_{.............................}

_{an-1 = an-1+R*an-2+L*a0}

_{3 根据第二条思路我们可以构造出如下的矩阵}

_{1 L 0 ...... R a0 a0'}

_{R 1 L ......... * a1 a1'}

_{................... .... = ......}

_{...........R 1 L an-2 an-2'}

_{L ...........R 1 an-1 an-1'}

_{4 那么根据3我们可以利用矩阵快速幂求出最后的答案，但是题目的n最大为100，m最大为10^9，那么每个case的时间复杂度为O(Logm*n^3)，当n最大为100的时候是会TLE的}

_{5 我们发现初始的矩阵里面，矩阵是一个循环同构的，就是说矩阵的每一行度能够从上一行推出，那么我们只要利用O(n^2)的时间求出第一行，然后我们在利用递推求出剩下的n-1行，那么总的时间复杂度为O(Logm*n^2)}

_{点击查看代码}

第二十题 hdu 4291 A Short problem

点击打开hdu 4291

思路: 循环节+矩阵快速幂

分析:

1 题目给定g(n) = 3*g(n-1)+g(n-2) , g(1) = 1 , g(0) = 0 , 要求g(g(g(n)))%10^9+7

2 最初的想法是从里面一层一层的求出g(n)，每一次都利用矩阵快速幂。但是发现嵌套的时候只有最外层是%(10^9+7)，但是里面两层如果%(10^9+7)的话答案是错的。

那么这里涉及到了循环节，最外层%(10^9+7)，肯定有个循环节L1。那么我们可以通过求出的L1找到第二层的循环节为L2，通过第二层的循环节L2找到第三层的循环节L3

3 找循环节我们利用暴力求出即可。然后我们回答最初的思路上，只要做三次的矩阵快速幂，然后把相应要mod上相应的值即可

点击查看代码

第二十一题 uva12470 Tribonacci

点击打开uva12470

思路: 矩阵快速幂

分析:

1 裸题

点击查看代码

第二十二题 hdu 2855 Fibonacci Check-up

点击打开hdu 2855

思路: 递推+矩阵快速幂

分析:

1 题目的意思是给定n和m，要求

2 这一题有两种思路，对于这种的题肯定是有递推式的，那么找不到递推式的时候我们尝试去打表

下面我打出了前几十项，发现了n >= 2的时候有f(n) = 3*f(n-1)-f(n-2)，那么我们可以利用矩阵快速幂求f(n)

3 另一种思路是考虑f(n) = f(n-1) + f(n-2)，那么我们可以利用矩阵求出任意的f(n)

1 1 * f(n-1) = f(n)

1 0 f(n-2) f(n-1)

那么对于n >= 2的时候，我们假设左边的矩阵为A，那么A^(n-1)即可求出答案

那么A^(n-1)为 f(n) f(n-1)

f(n-1) f(n-2)

那么根据我们知道二项式定理为(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)*b+C(n,2)a^(n-2)*b^2+...+C(n,n)b^n

那么我们发现所求的式子和上面很像，因为f(n)可以利用上面的A矩阵的n-1次方求出

那么原式所求变成(1+A)^n，这里的1为单位矩阵。因为做了n次方，那么最终的答案就是ans.mat[0][1] 或ans.mat[1][0]

点击查看代码

第二十三题 hdu 3658How many words

点击打开hdu 3658

思路: 递推+矩阵快速幂

分析:

1 题目的意思是在52个英文字母里面选择m个字母组成一个字符串，满足以下两个条件。第一是相邻的两个字符的ASCLL码的绝对值小于等于32，第二至少要有一对的字符的绝对值为32

2 那么不考虑第二个条件的时候，我们可以求出所有的符合的个数。假设f(n)(j)表示的是前n个字符最后一个字符为j，那么我们可以求出所有满足第一个条件的所有个数。因为至少需要有一对相邻的字符的绝对值为32，那么我们只要把第一次求出的所有的个数减去“相邻的两个字符的ASCLL码的绝对值小于等于31”的即可

3 那么我们考虑“相邻的两个字符的ASCLL码的绝对值小于等于32”这种情况，f(n)(j) =Σ(f(n-1)(k)) , abs(j-k) <= 32

那么我们可以构造出如下的矩阵

4 那么相邻的两个字符的ASCLL码的绝对值小于等于31就和上面的类似

点击查看代码

第二十四题 poj 3150Cellular Automaton

点击打开poj 3150

思路: 矩阵快速幂

分析:

1 题目给定n个数每个数在0～m-1之内，题目规定两个数之间的距离为min(|i-j| , n-|i-j|)。现在给定d和k，表示做k次的变换，每一次变换过后每个数变成了一个新的数。这个新的数等于和它距离小于等于d的所有数的和%m

2 这题和之前做的两道题很像hdu2276 和 FZU1692，都是属于循环同构的问题

那么我们先来看一下每个数在做一次变换过后变成什么。因为要距离小于等于d，第一种|i-j| = d , 则j = i+d , 第二种情况n-|i-j| = d , 因此 j = n-d+i 。

第一个数等于 = num[1]+num[2]+....+num[d+1]+num[n-d+1]+...+num[n]

第二个数等于 = num[2]+....+num[d+2]+num[n-d+2]+...+num[n]

..............................................................................................................

3 因为这里的矩阵是循环同构的，因此我们只要求出第一行，剩下的我们就可以根据前一行推出。这样就把矩阵的乘法的复杂度降到了O(n^2)

点击查看代码

第二十五题 poj 3735Training little cats

点击打开poj 3735

思路: 矩阵快速幂

分析:

1 题目给定n只猫，每只猫的初始的花生的数量为0。现在有三种操作，g i 第i只猫加一个花生，e i 把第i只猫的所有花生全部吃完 s i j 把第i 和 j只猫的花生数进行交换

2 根据上面的三种操作那么我们能够举例n = 3的时候的三种操作。

对于g 1，我们把第一行的最后一位加1，这里增加了一列目的是为了能够求出和，因为初始化a b c都为0

1 0 0 1 a a+1

0 1 0 0 * b = b

0 0 1 0 c c

0 0 0 1 1 1

对于e 1，我们把第一行全部置为0，那么这样就是相当于吃掉全部的花生

0 0 0 0 a 0

0 1 0 0 * b = b

0 0 1 0 c c

0 0 0 1 1 1

对于 s 1 2

0 1 0 0 a b

1 0 0 0 * b = a

0 0 1 0 c c

0 0 0 1 1 1

3 那么我们只要先把k次的操作整合到一个矩阵A里面，然后求A^m，矩阵的最后一列的前n个数即为所求

4 由于矩阵乘法涉及到乘的次数越多，就越耗时间，因此我们需要在矩阵相乘的时候进行优化

点击查看代码