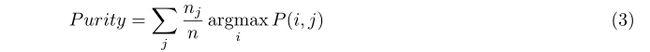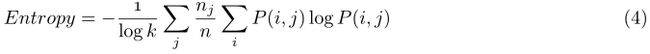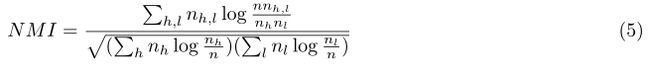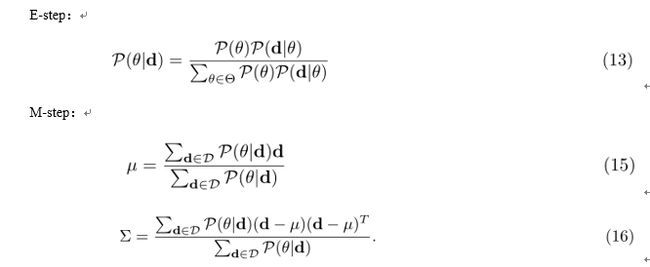文档聚类概述

前面我简单介绍了NMF在文档聚类上的应用。这次我会系统介绍一下文档聚类的一些内容，让大家有一个整体的印象。

1 绪论

 

文档聚类（或文本聚类）是更大领域的数据聚类的一个子集，从信息检索（IR）、自然语言处理（NLP）和机器学习(ML) 等领域借用概念。

一个好的文档聚类方法，计算机可以自动地将文档语料库组织成一个有意义的群集层次结构，从而使语料库高效浏览和导航。文档聚类可以产生不相交的或者重叠划分（软划分）。在重叠划分中，一个文档可能出现在多个类中，这种划分可以产生一个更好的聚类，因为一个文档通常会涉及多个主题。

要进行聚类首先必须考虑如何处理数据。大部分已存在的文档聚类方法选择将每一个文档表示为一个向量，这样就可以将文档聚类简化成为一个简单的数据聚类。向量模型的一个潜在缺点是没有考虑单词的出现次序。近来出现另外一种表示方法，在定义相似性时不仅考虑术语的出现还考虑术语一起或者序列出现的频率。第3部分会详细介绍文档模型。

Nicholas O.Andrews and Edward A. Fox（2007） [1] 将文档聚类算法分为区别（discriminative）和生成（generative）类型。广泛的说，区别算法在每一个文档之间的相似性上操作，然后基于这些相似性优化一个条件（目标）函数来产生一个最优聚类。而生成算法假定一个数据分布，最大化分布的匹配来产生聚类质心。第4和5部分会详细介绍两类算法。

从term-document矩阵得到的向量空间的另一个角度是相似度矩阵。在图论中，相似度矩阵定义了图中顶点之间的连通性。利用文档向量可以产生一个带权重的图。然后利用图的多路分割来产生一个聚类结果。这些方法会在第6部分中介绍。

选择向量来表示一个文档，那么 term-document 矩阵可能会变得很大。所以人们开始注意到降维聚类。第 7 部分会介绍几种代表性的降维方法。

2 评测

 

文档聚类已经利用多种方法评估了，但是并没有一致的意见说明哪个是最好的。评估的选择取决于研究领域。如AI领域通常选择mutual information，而IR领域选择F-measure。

两种直观的标准是准确率（precision）和召回率（recall）。在IR领域通常是将这两种标准结合在一起，即F-measure。R代表召回率，P代表准确率，一般化的F-measure可以表示为：

其中表示R和P的权重（重要性），可以取1,0.5,2等值。

为了将F-measure扩展到聚类中，我们假定存在一个由聚类算法输出的聚类结果（clusters）和引用类（classes，正确结果）集合。对于class i和cluster j，在聚类中定义F-measure：

其中n表示文档的数量。

另外两个测量是聚类purity和entropy。Purity测量在给定聚类中支配类成员的百分比（越大越好），entropy看的是在聚类（clusters）中每一个引用类（class）的文档分布（越小越好）。

其中P（i，j）表示聚类j（cluster）的成员属于一个类i（class）的概率。

上述给出的评估方法都是假设聚类的个数和引用类的个数相同，但是通常情况它们的数目不同，这种情况下mutual information比purity和entropy更好。在实际应用中MI正规化为单位长度（NMI）。表示class h中文档的数目，表示cluster 中样本的数目，表示在class h和cluster 中样本的数目，那么：

NMI的范围是[0,1]，1代表引用类和聚类之间完全匹配。NMI是对引用类个数和聚类个数之间不匹配容忍的一种准确度测量。

另一种对聚类算法质量的视角是划分的稳定性。一个直观的测量稳定性的方法是看平均性能。就mutual information来说，让表示r个聚类的集合，表示一个聚类，那么平均NMI（ANMI）可以定义为：

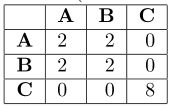
另外一种不常出现在文献的测量方法是冲突矩阵，它是一种可视化工具来提供误分类总结。如：

表1：类 A (4个元素), B (4个元素), 和 C (8个元素)的冲突矩阵

上面所描述的测量都是为不相交聚类的。评估模糊聚类的通常方法时从模糊输出中产生一个硬聚类。通常是利用一个阈值来确定一个文档属于哪个类，如果一个文档在两个类或者多个类中的可能性均大于阈值那么这个文档将出现在多个类中。

      

3 数据处理模型

3.1  向量空间模型

在向量空间模型下，n个文档，m个术语被表示成为一个mn的term-document矩阵，每一个文档是一个m维的向量。

3.2 基于短语的模型

考虑短语“the dog chased a cat”和“the cat chased adog”。如果转化为向量的话，都是{chase，cat，dog}但是它们的意义明显不一样。所以有的人就假设将单词的次序信息加入到聚类中能改善聚类的准确率。

下面我们介绍一种基于短语的模型。

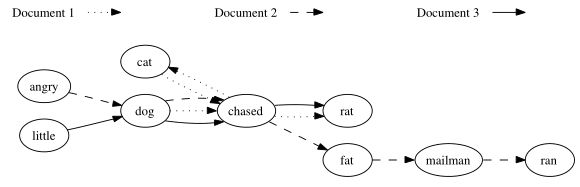
文档索引图（DIG）在2004年由K. M.Hammouda 和 M. S.Kamel[18]提出，是基于单词次序匹配来定义相似度的。

DIG是一个多路有向图，每一个顶点表示一个单词。图的边表示单词的序列，每一个顶点都维护出现该词的文档列表，以及通过记录边的连续性来维护句子信息。如果一个单词在一个文档中出现多次，那么它在图中对应顶点的频率次数也相应增加。如图1是一个DIG例子。

图1：文档1包含“catchased rat” 和 “dogchased cat”。文档2包含“angrydog chased fat mailman” 和“mailman ran”。文档3包含“littledogchased rat”。有向边表示一个句子。

   DIG将单词作为顶点存储，并在每个顶点维护频率信息,从而避免存储冗余信息。DIG不是一种聚类算法，只是一个利用有向边存储单词次序信息的文档模型。在这种模型下，基于重叠子图的相似度可以得到计算进而获得一个相似度矩阵。这种相似度矩阵可以利用任何一种谱算法或者区分算法进行聚类。

   结合单词次序信息与单词频率可以改进聚类的精确性，根据研究大概有20%的提高。然而，应该指出是关联这两种信息是有一定的花销的。如果可以预计算相似性矩阵，那么这种混合方法在效率上是相当于传统方法。另一方面，如果联机检索文档，DIG的建立是有一点昂贵的。

4 区分算法

区分算法是基于文档向量两两相似度的一类算法，其中层次聚类算法和划分算法是主要的聚类方法。

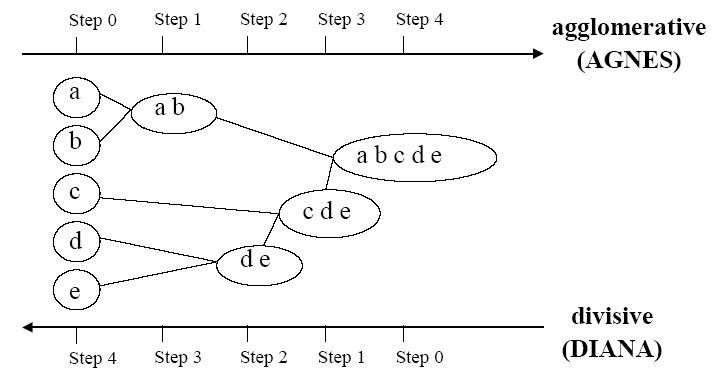
层次聚类算法又称为树聚类算法[3,4,19]，它使用数据的联接规则，透过一种层次架构方式，反复将数据进行分裂或聚合，以形成一个层次序列的聚类问题解。层次算法的计算复杂性为，适合于小型数据集的分类。层次聚类算法又可以分为凝聚的方法(agglomerative)，也称自底向上（bottom-up）和分裂的方法（divisive），也称自顶向下（top-down）。图2是对层次聚类的表示。

层次方法应用于需要层次结构的应用，能够产生较高质量的聚类。

但是层次算法的时间复杂度和空间复杂度很高，严重限制了数据集的大小；缺乏全局目标函数；所有合并都是最终的，无法撤销，对于噪声、高维数据可能造成问题。

图2：层次聚类

 

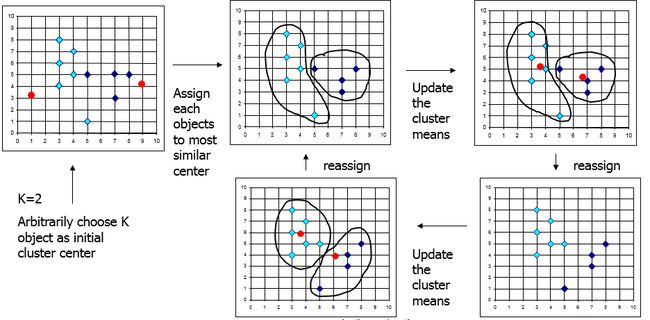
划分式聚类算法需要预先指定聚类数目或聚类中心，通过反复迭代运算，逐步降低目标函数的误差值，当目标函数值收敛时，得到最终聚类结果。如对包含n个文档的文本集合，划分将生成k个分组，k<=n，每一个分组代表一个聚类。划分算法比层次算法要有更好的性能。典型的划分方法包括k-means及其变形等。

图3：k-means聚类过程

 

K-means中相似度是根据欧氏距离，而对于文档聚类中cosine相似度要好于欧式距离，这种算法称作sphericalkmeans[5]。

k-means实现简单，可用于多种类型，空间需求适度，时间复杂度也适度，复杂度是，n是文档的数目，k是聚类数目，l是迭代次数。

kmeans算法有着一些问题：它依赖于随机的初始化；它可能收敛于局域最小值；易受到离群点和噪音的影响；对数据点的分布有一定的假设，不适合用于发现非凸形状（非球形）的聚类，或具有各种不同大小（不同尺寸、不同密度）的聚类。

5 生成算法

生成算法，基于模型方法为每个聚类假设一个模型，然后再去发现符合相应模型的数据对象。一个基于模型的算法可以通过构造一个描述数据点空间分布的密度函数来确定具体聚类。它利用迭代过程在模型估计与文档分配步骤之间交替变换。

每一种模型都提供了文档属于每一个类的概率计算（密度函数）方法。通常使用的模型有高斯模型和冯米塞斯费舍尔模型。

为了最大化总概率我们通常利用em算法[6]。EM算法是一种高效的解决模型中最大似然函数的迭代过程。它包含两个过程：E-step和M-step。E-step利用已知的数据和模型（聚类）的当前评估来计算丢失的数据（计算概率），M-step最大化似然函数，并调整参数。

在生成算法中，E-step只要是利用模型中给出的文档属于每一个类的概率（等式11和等式17）来计算似然概率P，M-step只要是调整参数来得到最大化概率的效果。

基于模型的算法根据标准统计方法并考虑到“噪声”或异常数据，可以自动确定聚类个数；模型多种多样，可供选择性高；可以发现不同大小和椭球形状簇；许多实际的数据是随机的，因此很大程度上满足模型的统计假设。

EM算法可能很慢，对于具有大量分量的模型不适合；当簇只包含少量数据点，或者数据点近似协线性时，也无法很好处理；如何选择正确模型存在问题。

6 谱聚类

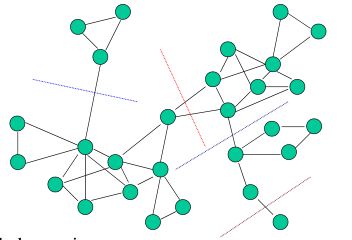
顶点之间的相似信息可以自然地表示为一个矩阵，向量模型可以解释成为一个图。谱聚类涉及在图中寻找一个切割来产生好的聚类。如图4和5。

图4：一个多路分割示意图

 

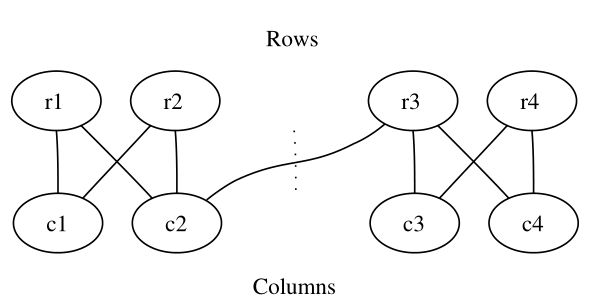
图5：二分图分割。虚线表示一个分割，产生一个同时对term-document的行和列联合聚类。

 

问题是如何在图中寻找到好的分割？这就出现了大量的准则函数，谱聚类算法需要最优化它们来得到好的分割。其中最常用的包括多路ratio cut，normalized cut（NCut）和max-min cut。这些不同目标函数的求解可能会用到特征值（特征向量）或者奇异值（奇异向量）。

对于ratio cut，normalized cut（NCut）和max-min cut，如果集群是很好的分离,所有三个不同的分割都会给出一个非常相似的和准确的结果；当集群是略微分开的，NCut和max-min cut会给出更好的结果；当集群明显地重叠，max-min cut往往给更紧凑平衡集群[7]。

7 降维

 

尽管预处理可以实现向量空间的大小显著减少,但后检索应用程序要求更高的效率。因此我们需要更好的降维算法。这部分我们介绍三种最常用的降维技术，它们不仅可以显著地减少文档向量的大小，还能提高聚类的准确率。实际上这些方法本身也可以看作是聚类方法。

7.1 主成分分析（PCA）

      PCA[8]是一个著名的维度降低算法，离散K-L装换是它的理论基础。

主成分分析有两个重要的属性,这些属性使它适合聚类:近似和可区别性。近似是说PCA在降维的同时，引进了一个可控制的误差使得近似最优化。另外实验表明PCA使得相似的文档更加相似，不相似的文档更加不相似，增加了可区分性这使得聚类更加容易。

当然PCA也有一系列的问题。（1）近似得到结果中包含负值,所以降维的空间不能直接解释为一个聚类，但是可以在降维的空间上执行传统的聚类方法(如k-means)产生最后的聚类结果,而且它实际上生产聚类比直接在原来的向量空间上进行更准确；（2）另一个问题是,主成分是正交的。这是对于文本数据是有问题的,如文档可能跨越多个主题,所以在这种情况潜在的语义变量将不会是正交的；（3）计算协方差矩阵的特征值和特征向量时间花销是很大的，而且不能迭代的进行求解，使得奇异值分解的求解不是一个优化过程也无法产生一个中间值。

7.2 奇异值分解（SVD）  

   可以看出SVD与PCA相似[9]，只是在计算特征空间上略有区别，所以它和PCA有着共同的优点和问题。

7.3 非负矩阵分解（NMF）

   非负矩阵分解(NMF)[10],原本为计算机视觉应用,已经被有效地用于文档聚类[2]。NMF产生的近似矩阵只包含非负的因素,这意味着可以从降维的空间直接得到一个可解释的聚类而不需要进一步的后处理。

和上述两种降维方法相比，NMF不需要派生的潜在语义空间是正交的，并且保证每个文档在所有潜在语义方向上都取非负值。并且NMF有以下优点：

（1）当聚类之间存在重叠，NMF 仍然可以为每个聚类找到潜在的语义方向，而由奇异值分解的正交要求或特征向量计算使得派生潜在语义的方向，不太可能对应于每个聚类。

（2）利用NMF，一个文档是基础潜在语义的加法的组合，使得在文本域中更有意义。

（3）每个文档的聚类成员可以直接从 NMF的结果中得到，而从谱聚类所得的潜在语义空间对每个数据点的分布不提供直接指示，因此，必须利用传统的数据聚类 K-均值等方法来找到最终的文档聚类结果。

8 总结

文档聚类算法有多种多样，每一种算法都有自己的优缺点，并不能说哪一种算法是最好的，哪一种算法是最坏的，根据不同的应用选择适合的算法才是正确的。比如小规模的聚类，由于它的简单易于实现等特点选择k-means会更好，又比如对于大规模的数据聚类，先对元数据进行降维处理会取得更好的效率和准确率。

参考文献：

[1] Andrews, Nicholas O. and Fox, Edward A. Recent Developments inDocument Clustering.Technical Report TR-07-35, Computer Science, VirginiaTech, 2007.

[2] Wei Xu, Xin Liu, YihongGong.Document Clustering Based On Non-negative Matrix factorization .In Proceedings of the 26th annualinternational ACM SIGIR conference on Research and development in informaionretrieval, 2003, pp. 267-273.

[3] Marques JP,Written; Wu YF, Trans. Pattern Recognition Concepts, Methods and Applications.2nd ed., Beijing: Tsinghua University Press, 2002. 51−74 (in Chinese).

[4] Fred ALN, LeitãoJMN. Partitional vs hierarchical clustering using a minimum grammar complexityapproach. In: Proc. of the SSPR&SPR 2000. LNCS 1876, 2000, pp. 193−202.

[5] Inderjit S.Dhillon and Dharmendra S. Modha. Concept decompositions for large sparse textdata using clustering. Mach. Learn., 2001, 42(1-2):143–175.

[6] R. Neal and G.Hinton. A view of the em algorithm that justifies incremental, sparse, andother variants.In M. I. Jordan, editor, Learning in Graphical Models. Kluwer,1998.

[7] Chris H. Q.Ding, Xiaofeng He, Hongyuan Zha, Ming Gu, and Horst D. Simon. A min-max cutalgorithm for graph partitioning and data clustering. In ICDM ’01: Proceedingsof the 2001 IEEE International Conference on Data Mining, pages 107–114,Washington, DC, USA, 2001. IEEE Computer Society.

[8] M. Turk and A.Pentland. Eigenfaces for recognition. Journal of Cognitive Neuroscience, vol.26, 2004, pp. 71-86.

[9]Wall, Michael E., Andreas Rechtsteiner, LuisM. Rocha.  Singular value decompositionand principal component analysis. In D.P. Berrar, W. Dubitzky, M. Granzow. APractical Approach to Microarray Data Analysis. Norwell, MA: Kluwer. 2003, pp.91–109.

[10] Daniel D. Leeand Sebastian H. Seung. Learning the parts of objects by non-negative matrixfactorization. Nature, 401(6755):788–791, October 1999.

[11] Dee, D.D. &Seung, H.S.. Algorithms for Non-negative Matrix Factorization. Advances inNeural Information Processing, 13, 2001.

[12] Kim, H. &Park, K.. Non-negative Matrix Factorization Based on Alternating Non-negativityConstrained Least Squares and Active Set Method. SIAM J. Matrix Anal. Appl.,30(2), 2008, pp.713–730.

[13] Cichocki, A.,Zdunek, R. & Amari, S.. Hierarchical ALS Algorithms for Nonnegative Matrixand 3D Tensor Factorization. Lecture Notes in Computer Science, Springer, 4666,2007, pp.169–176.

[14] Cichocki, A.,Zdunek, R. & Amari, S.. Non-negative Matrix Factorization with Quasi-NewtonOptimization. Lecture Notes in Artificial Intelligence, Springer, 4029, 2006,pp.870–879.

[15] Lin, C.-J..Projected Gradient Methods for Nonnegative Matrix Factorization. NeuralComputation,MIT press, 19, 2007, pp.2756–2779.

[16]Gillis, N.. Nonnegative Matrix Factorization:Complexity, Algorithms and Applications. Université catholique de Louvain, PhDThesis, 2011.

[17] NicolasGillis1an,Francois Glineur. Accelerated Multiplicative Updates and HierarchicalALS Algorithms for Nonnegative Matrix Factorization. Neural Computation,2011.

[18] K. M. Hammouda and M. S. Kamel. Efficient phrase-baseddocument indexing for web document clustering. IEEE Transactions on knowledgeand data engineering, 16(10):1279–1296, 2004.