Redis 的底层数据结构(跳跃表)
我们都知道单链表有一个致命的弱点,查找任一节点都至少 O(n) 的时间复杂度,它需要遍历一遍整个链表,那么有没有办法提升链表的搜索效率?
跳跃表(SkipList)这种数据结构使用空间换时间的策略,通过给链表建立多层索引来加快搜索效率,我们先介绍跳跃表的基本理论,再来看看 redis 中的实现情况。
一、跳跃表(SkipList)

这是一条带哨兵的双端链表,大部分场景下的链表都是这种结构,它的好处是,无论是头插法还是尾插法,插入操作都是常量级别的时间复杂度,删除也是一样。但缺点就是,如果想要查询某个节点,则需要 O(n)。
那如果我们给链表加一层索引呢?当然前提是最底层的链表是有序的,不然索引也没有意义了。
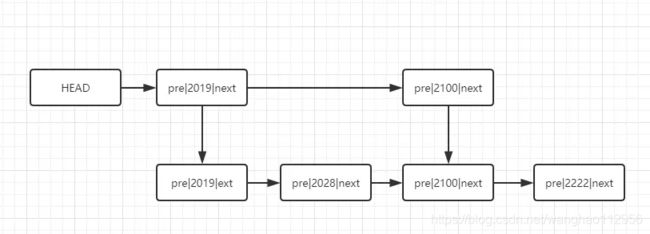
让 HEAD 头指针指向最高索引,我抽出来一层索引,这样即便你查找节点 2222 三次比较。
第一次:与 2019 节点比较,发现大于 2019,往后继续
第二次:与 2100 节点比较,发现依然大于,往后继续
第三次:本层索引到头了,指向低层索引的下一个节点,继续比较,找到节点
而无索引的链表需要四次,效率看起来不是很明显,但是随着链表节点数量增多,索引层级增多,效率差距会很明显。图就不自己画了,取自极客时间王争老师的一张图。
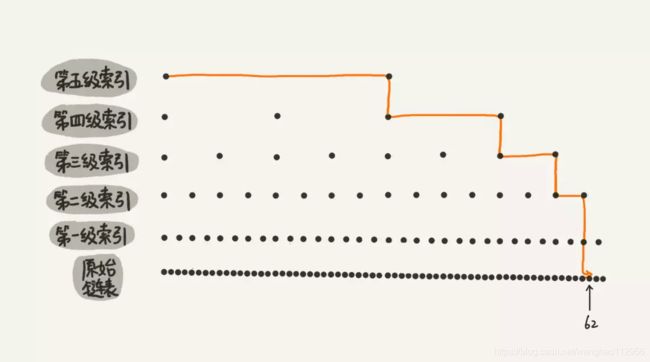
你看,原本需要 62 次比较操作,通过五层索引,只需要 4 次比较,跳跃表的效率可见一瞥。
想要知道具体跳跃表与链表差距多少,我们接下来进行它们各个操作的时间复杂度分析对比。
1、插入节点操作
双端链表(以下我们简称链表)的原本插入操作是 O(1) 的时间复杂度,但是这里我们讨论的是有序链表,所以插入一个节点至少还要找到它该插入的位置,然后才能执行插入操作,所以链表的插入效率是 O(n)。
跳跃表(以下我们简称跳表)也依然是需要两个步骤才能完成插入操作,先找到该插入的位置,再进行插入操作。我们设定一个具有 N 个节点的链表,它建有 K 层索引并假设每两个节点间隔就向上分裂一层索引。
k 层两个节点,k-1 层 4 个节点,k-2 层 8 个节点 … 第一层 n 个节点,
1:n
2:1/2 * n
3:1/2^2 * n
.....
.....
k:1/2^(k-1) * n
1/2^(k-1) * n 表示第 k 层节点数,1/2^(k-1) * n=2 可以得到,k 等于 logn,也就是说 ,N 个节点构建跳表将需要 logn 层索引,包括自身那层链表层。
而当我们要搜索某个节点时,需要从最高层索引开始,按照我们的构建方式,某个节点必然位于两个索引节点之间,所以每一层都最多访问三个节点。这一点你可能需要理解理解,因为每一层索引的搜索都是基于上一层索引的,从上一层索引下来,要么是大于(小于)当前的索引节点,但不会大于(小于)其往后两个位置的节点,也就是当前索引节点的上一层后一索引节点,所以它最多访问三个节点。
有了这一结论,我们向跳表中插入一个元素的时间复杂度就为:O(logn)。这个时间复杂度等于二分查找的时间复杂度,所有有时我们又称跳表是实现了二分查找的链表。
很明显,插入操作,跳表完胜链表。
2、修改删除查询
这三个节点操作其实没什么可比性,修改删除操作,链表等效于跳表。而查询,我们上面也说了,链表至少 O(n),跳表在 O(logn)。
除此之外,我们都知道红黑树在每次插入节点后会自旋来进行树的平衡,那么跳表其实也会有这么一个问题,就是不断的插入,会导致底层链表节点疯狂增长,而索引层依然那么多,极端情况所有节点都新增到最后一级索引节点的右边,进而使跳表退化成链表。
简单一句话来说,就是大量的节点插入之后,而不更新索引的话,跳表将无法一如既往的保证效率。解决办法也很简单,就是每一次节点的插入,触发索引节点的更新,我们具体来看一下更新策略。
一般跳表会使用一个随机函数,这个随机函数会在跳表新增了一个节点后,根据跳表的目前结构生成一个随机数,这个数值当然要小于最大的索引层值,假定这个值等于 m,那么跳表会生成从 1 到 m 层的索引。所以这个随机函数的选择或者说实现就显得很重要了,关于它我们这里不做讨论,大家可以看看各种跳表的实现中是如何实现这个随机函数的,典型的就是 Java 中 ConcurrentSkipListMap 内部实现的 SkipList 结构,当然还有我们马上要介绍的 redis 中的实现。
以上就是跳表这种数据结构的基本理论内容,接下来我们看 redis 中的实现情况。
二、Redis 中的跳跃表
说在前面的是,redis 自己实现了跳表,但目的是为它的有序集合等高层抽象数据结构提供服务,所以等下我们分析源代码的时候其中必然会涉及到一些看似无用的结构和代码逻辑,但那些也是非常重要的,我们也会提及有序集合相关的内容,但不会拆分细致,重点还是看跳表的实现。
跳表的数据结构定义如下:
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
跳表中的每个节点用数据结构 zskiplistNode 表示,head 和 tail 分别指向最底层链表的头尾节点。length 表示当前跳表最底层链表有多少个节点,level 记录当前跳表最高索引层数。
zskiplistNode 结构如下:
typedef struct zskiplistNode {
sds ele;
double score;
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned int span;
} level[];
} zskiplistNode;
我这里摘取的 redis 源码是 4.0 版本的,以前版本 ele 属性是一个 RedisObject 类型,现在是一个字符串类型,也即表示跳表现在只用于存储字符串数据。
score 记录当前节点的一个分值,最底层的链表就是按照分值大小有序的串联的,并且我们查询一个节点,一般也会传入该节点的 score 值,毕竟数值类型比较起来方便。
backward 指针指向前一个节点,为什么是倒着往前,我们待会会说。
level 是比较关键的一个点,这里面是一个 level 数组,而每个元素又都是一个 zskiplistLevel 类型的结构,zskiplistLevel 类型包括一个 forward 前向指针,一个 span 跨度值,具体是什么意思,我们一点点说。
跳表理论上在最底层是一条双端链表,然后基于此建立了多层索引节点以实现的,但在实际的代码实现上,这种结构是不好表述的,所以你要打破既有的惯性思维,然后才能好理解 redis 中的实现。实际上正如我们上述介绍的 zskiplistNode 结构一样,每个节点除了存储节点自身的数据外,还通过 level 数组保存了该节点在整个跳表各个索引层的节点引用,具体结构就是这样的:
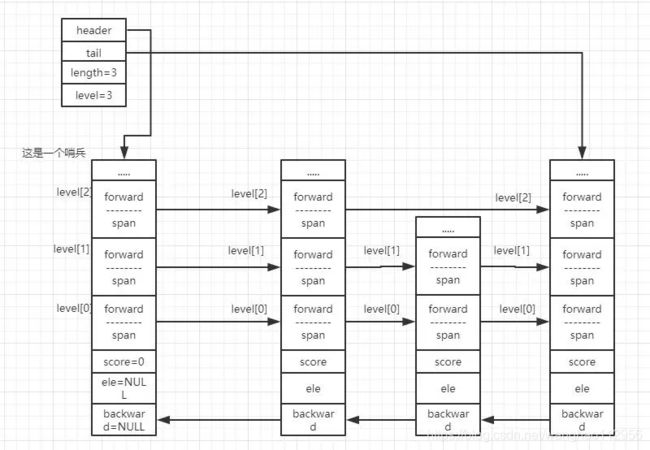
每一个节点的 backward 指针指向自己前面的一个节点,而每个节点中的 level 数组记录的就是当前节点在跳表的哪些索引层出现,并通过其 forward 指针顺序串联这一层索引的各个节点,0 表示第一层,1 表示第二层,等等以此类推。span 表示的是当前节点与后面一个节点的跨度,我们等下还会在代码里说到,暂时不理解也没关系。
基本上跳表就是这样一个结构,上面那张图还是很重要的,包括我们等下介绍源码实现,也对你理解有很大帮助的。(毕竟我画了半天。。)
这里多插一句,与跳表相关结构定义在一起的还有一个有序集合结构,很多人会说 redis 中的有序集合是跳表实现的,这句话不错,但有失偏驳。
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
准确来说,redis 中的有序集合是由我们之前介绍过的字典加上跳表实现的,字典中保存的数据和分数 score 的映射关系,每次插入数据会从字典中查询,如果已经存在了,就不再插入,有序集合中是不允许重复数据。
下面我们看看 redis 中跳表的相关代码的实现情况。
1、跳表初始化
redis 中初始化一个跳表的代码如下:
zskiplistNode *zslCreateNode(int level, double score, sds ele) {
zskiplistNode *zn =
zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
zn->score = score;
zn->ele = ele;
return zn;
}
/* Create a new skiplist. */
zskiplist *zslCreate(void) {
int j;
zskiplist *zsl;
//分配内存空间
zsl = zmalloc(sizeof(*zsl));
//默认只有一层索引
zsl->level = 1;
//0 个节点
zsl->length = 0;
//1、创建一个 node 节点,这是个哨兵节点
//2、为 level 数组分配 ZSKIPLIST_MAXLEVEL=32 内存大小
//3、也即 redis 中支持索引最大 32 层
zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
//为哨兵节点的 level 初始化
for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
zsl->header->level[j].forward = NULL;
zsl->header->level[j].span = 0;
}
zsl->header->backward = NULL;
zsl->tail = NULL;
return zsl;
}
zslCreate 用于初始化一个跳表,比较简单,我也给出了基本的注释,这里不再赘述了,强调一点的是,redis 中实现的跳表最高允许 32 层索引,这么做也是一种性能与内存之间的衡量,过多的索引层必然占用更多的内存空间,32 是一个比较合适值。
2、插入一个节点
插入一个节点的代码比较多,也稍微有点复杂,希望你也有耐心和我一起来分析。
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
//update数组将用于记录新节点在每一层索引的目标插入位置
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
//rank数组记录目标节点每一层的排名
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
//指向哨兵节点
x = zsl->header;
//这一段就是遍历每一层索引,找到最后一个小于当前给定score值的节点
//从高层索引向底层索引遍历
for (i = zsl->level-1; i >= 0; i--) {
//rank记录的是节点的排名,正常情况下给它初始值等于上一层目标节点的排名
//如果当前正在遍历最高层索引,那么这个初始值暂时给0
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
//我们说过level结构中,span表示的是与后面一个节点的跨度
//rank[i]最终会得到我们要找的目标节点的排名,也就是它前面有多少个节点
rank[i] += x->level[i].span;
//挪动指针
x = x->level[i].forward;
}
update[i] = x;
}
//至此,update数组中已经记录好,每一层最后一个小于给定score值的节点
//我们的新节点只需要插在他们后即可
//random算法获取一个平衡跳表的level值,标志着我们的新节点将要在哪些索引出现
//具体算法这里不做分析,你也可以私下找我讨论
level = zslRandomLevel();
//如果产生值大于当前跳表最高索引
if (level > zsl->level) {
//为高出来的索引层赋初始值,update[i]指向哨兵节点
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
//根据score和ele创建节点
x = zslCreateNode(level,score,ele);
//每一索引层得进行新节点插入,建议对照我之前给出的跳表示意图
for (i = 0; i < level; i++) {
//断开指针,插入新节点
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
//rank[0]等于新节点再最底层链表的排名,就是它前面有多少个节点
//update[i]->level[i].span记录的是目标节点与后一个索引节点之间的跨度,即跨越了多少个节点
//得到新插入节点与后一个索引节点之间的跨度
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
//修改目标节点的span值
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
//如果上面产生的平衡level大于跳表最高使用索引,我们上面说会为高出部分做初始化
//这里是自增他们的span值,因为新插入了一个节点,跨度自然要增加
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
//修改 backward 指针与 tail 指针
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
zsl->length++;
return x;
}
整个方法我都已经给出了注释,具体的不再细说,欢迎你与我交流讨论,整体的逻辑分为三个步骤。
- 从最高索引层开始遍历,根据 score 找到它的前驱节点,用 update 数组进行保存
- 每一层得进行节点的插入,并计算更新 span 值
- 修改 backward 指针与 tail 指针
删除节点也是类似的,首先需要根据 score 值找到目标节点,然后断开前后节点的连接,完成节点删除。
3、特殊的查询操作
因为 redis 的跳表实现中,增设了 span 这个跨度字段,它记录了与当前节点与后一个节点之间的跨度,所以就具有以下一些查询方法。
a、zslGetRank
返回包含给定成员和分值的节点在跳跃表中的排位。
unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {
zskiplistNode *x;
unsigned long rank = 0;
int i;
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) <= 0))) {
rank += x->level[i].span;
x = x->level[i].forward;
}
/* x might be equal to zsl->header, so test if obj is non-NULL */
if (x->ele && sdscmp(x->ele,ele) == 0) {
return rank;
}
}
return 0;
}
你会发现,这个方法的核心代码其实就是我们插入节点方法的一个部分,通过累计 span 得到目标节点的一个排名值。
b、zslGetElementByRank
通过给定排名查询元素。这个方法就更简单了。
c、zslIsInRange
给定一个分值范围(range), 比如 0 到 10, 如果给定的分值范围包含在跳跃表的分值范围之内, 那么返回 1 ,否则返回 0 。
d、zslFirstInRange
给定一个分值范围, 返回跳跃表中第一个符合这个范围的节点。
e、zslDeleteRangeByScore
给定一个分值范围, 删除跳跃表中所有在这个范围之内的节点。
f、zslDeleteRangeByRank
给定一个排名范围, 删除跳跃表中所有在这个范围之内的节点。
其实,后面列出来的那些根据排名,甚至一个范围查询删除节点的方法,都仰仗的是 span 这个字段,这也是为什么 insert 方法中需要通过那么复杂的计算逻辑对 span 字段进行计算的一个原因。
总结一下,跳表是为有序集合服务的,通过多层索引把链表的搜索效率提升到 O(logn)级别,但修改删除依然是 O(1),是一个较为优秀的数据结构,而 redis 中的实现把每个节点实现成类似楼房一样的结构,也即我们的索引层,非常的巧妙。
(想自学习编程的小伙伴请搜索圈T社区,更多行业相关资讯更有行业相关免费视频教程。完全免费哦!)
