Merkle Tree 实现细节及（不）存在性证明

Merkle Tree in BitCoin & BitCoin Cash

Merkel Tree是Bitcoin的核心组件，其相关资料已经非常丰富，所以本文档偏重于介绍Merkle Tree的存在性证明与不存在性证明，并且铺垫一下Merkle Tree在Bitcoin中起的作用和开发中容易被忽视的一些细节。

Merkle Trees in Bitcoin

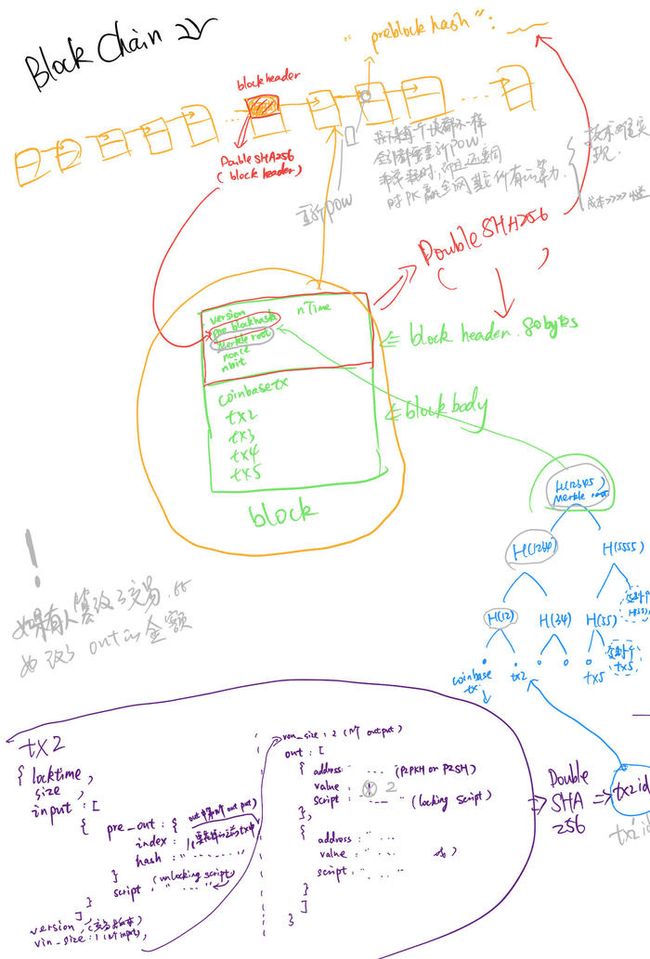
Merkle trees是以它的创造者 Ralph Merkle命名的。在Bitcoin的白皮书中得知，Merkle Trees的引入是将一个区块中所有的交易进行整合生成然后整个交易集合的数字指纹，从而确保的BTC不可篡改性。说一下自己理解的不可篡改性：

Bitcoin 借用Merkle Trees的结构从而实现了仅仅 256-bit 的Merkle Root即可“看管”住近1M的交易信息（BCH 为 32M）。一旦被篡改，立刻反映到块头，从而当前块以及当前块之后的每一块都要受到影响，并且这个”改变”貌似对你没有任何好处，因为比特币的非对称加密机制可以阻止你盗窃别人的比特币, 你只能开一条不被其他矿场认可的新链。这样的话即使你拥有巨大的算力，如果你稍微有理性的,你就不会去篡改比特币区块链, 所以说比特币从技术和动机两个方面打消了别人篡改比特币数据的念头。

比特币系统中的 Merkle Tree的计算其实包含有一些很隐晦的细节，这些细节很重要，它们会影响到整个计算结果的正确性, 在Bitcoin Wiki 中 ‘Protocol_documentation’提到过：

Note: Hashes in Merkle Tree displayed in the Block Explorer are of little-endian notation. For some implementations and calculations, the bytes need to be reversed before they are hashed, and again after the hashing operation.

Hashes以小端的形式（byte数组）进行hash运算，以大端形式（Hash值）展示给人看。

gcash中源码中hash.go存在相应佐证：

hash, err := chainhash.NewHashFromStr(str)

// NewHashFromStr creates a Hash from a hash string.  The string should be
// the hexadecimal string of a byte-reversed hash, but any missing characters
// result in zero padding at the end of the Hash.
func NewHashFromStr(hash string) (*Hash, error) {
    ret := new(Hash)
    err := Decode(ret, hash)
    if err != nil {
        return nil, err
    }
    return ret, nil
}

// Decode decodes the byte-reversed hexadecimal string encoding of a Hash to a
// destination.
func Decode(dst *Hash, src string) error {
    // Return error if hash string is too long.
    if len(src) > MaxHashStringSize {
        return ErrHashStrSize
    }

    // Hex decoder expects the hash to be a multiple of two.  When not, pad
    // with a leading zero.
    var srcBytes []byte
    if len(src)%2 == 0 {
        srcBytes = []byte(src)
    } else {
        srcBytes = make([]byte, 1+len(src))
        srcBytes[0] = '0'
        copy(srcBytes[1:], src)
    }

    // Hex decode the source bytes to a temporary destination.
    var reversedHash Hash
    _, err := hex.Decode(reversedHash[HashSize-hex.DecodedLen(len(srcBytes)):], srcBytes)
    if err != nil {
        return err
    }

    // Reverse copy from the temporary hash to destination.  Because the
    // temporary was zeroed, the written result will be correctly padded.
    for i, b := range reversedHash[:HashSize/2] {
        dst[i], dst[HashSize-1-i] = reversedHash[HashSize-1-i], b
    }

    return nil
}

newHash := HashMerkleBranches(hash1, hash2)

func HashMerkleBranches(left *chainhash.Hash, right *chainhash.Hash) *chainhash.Hash {
    // Concatenate the left and right nodes.
    var hash [chainhash.HashSize * 2]byte
    copy(hash[:chainhash.HashSize], left[:])
    copy(hash[chainhash.HashSize:], right[:])

    newHash := chainhash.DoubleHashH(hash[:])
    return &newHash
}

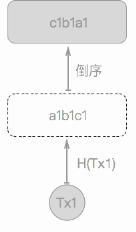
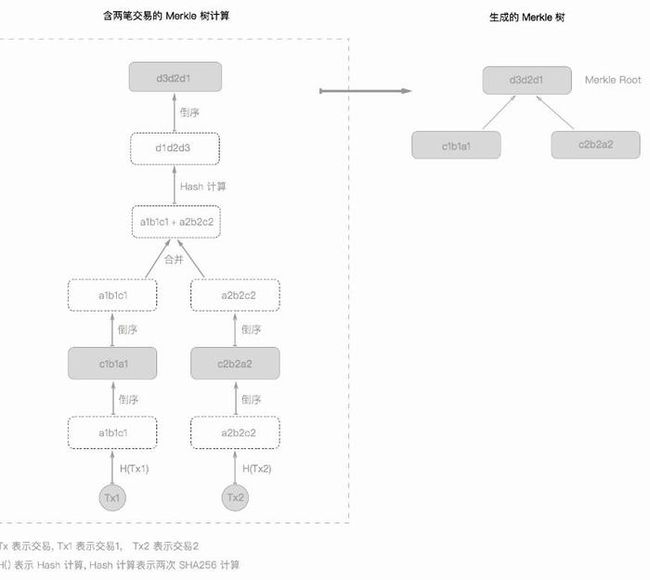
用图可以更直观理解来这些Merkle Tree的计算过程隐晦的细节：

含一笔交易的Merkle树计算

 

Merkle Trees Inclusive Verification

Merkle Trees除了不可篡改性起重要作用，也提供了SPV（Simplified Payment Verification）节点即使不用全部下载交易信息也能验证交易的方案。
在bitcoin wiki 中这样解释SPV的：

As noted in Nakamoto's whitepaper, it is possible to verify bitcoin payments without running a full network node. And this is called simplified payment verification or SPV. A user or user’s bitcoin spv wallet only needs a copy of the block headers of the longest chain, which are available by querying network nodes until it is apparent that the longest chain has been obtained. Then, wallet using spv client get the Merkle branch linking the transaction to its block. Linking the transaction to a place in the active chain demonstrates that a network node has accepted it, and blocks added after it further establish the confirmation.hain headers connect together correctly and that the difficulty is high enough

简单地来说 SPV 节点并不会下载全部的区块链数据，而只是下载块头，这条链并不包括交易数据. 当前的某个时刻比特币区块链的高度是 550387, 一个区块头的大小是 80 个字节, 那么由区块头组成的链的大小大概是 42 M, 这和整个区块链动辄上几百 G 的数据相比少了很多很多。

交易验证而言，SPV节点不会所有交易都去验证，它只对没有验证的与它相关的交易进行验证，于是SPV节点会设置一个filter只去接受匹配它设置的fliter的交易。比如：
SPV接收到一笔钱，并不能确认这个交易是否合法，因此要对这个交易的输入进行验证。SPV要拿着这个交易的信息向网络发起查询请求getdata（用MSG_MERKLEBLOCK标示），这个请求的响应被称为merkle block message。
当有全节点收到这个MSG_MERKLEBLOCK请求之后，利用传过来的交易信息在自己的区块链数据库中进行查询，并把验证路径返回给请求源，SPV节点拿到验证路径之后，再做一次merkle校验，

验证过程分两阶段：

1. 验证transaction是否在相应的block里（验证tx～block，即本文Merkle Trees Inclusive Verification）
2. 验证该block后是否在主链上，并且等待到其后是链上了6个或6个以上block才认为其不会被回滚掉（验证block～主链最长链block chain）。

确认无误之后，就认为这个交易是可信的。

这里我们假设这个全节点是诚实节点（实际上在p2p网络中，不可以相信任何节点），这里假设是为了解释后面存在性证明。

存在性证明的第一步就是解析merkle block message。所以我们先看一下SPV节点接收到的merkle block message：
摘自Bitcoin Developer Reference 的 Merkle Block Message部分

The merkleblock message is a reply to a getdata message which requested a block using the inventory type MSG_MERKLEBLOCK. It is only part of the reply: if any matching transactions are found, they will be sent separately as tx messages.
If a filter has been previously set with the filterload message, the merkleblock message will contain the TXIDs of any transactions in the requested block that matched the filter, as well as any parts of the block’s merkle tree necessary to connect those transactions to the block header’s merkle root. The message also contains a complete copy of the block header to allow the client to hash it and confirm its proof of work.

解析之后 结果如下：

01000000 ........................... Block version: 1
82bb869cf3a793432a66e826e05a6fc3
7469f8efb7421dc88067010000000000 ... Hash of previous block's header
7f16c5962e8bd963659c793ce370d95f
093bc7e367117b3c30c1f8fdd0d97287 ... Merkle root
76381b4d ........................... Time: 1293629558
4c86041b ........................... nBits: 0x04864c * 256**(0x1b-3)
554b8529 ........................... Nonce

07000000 ........................... Transaction count: 7
04 ................................. Hash count: 4

3612262624047ee87660be1a707519a4
43b1c1ce3d248cbfc6c15870f6c5daa2 ... Hash #1
019f5b01d4195ecbc9398fbf3c3b1fa9
bb3183301d7a1fb3bd174fcfa40a2b65 ... Hash #2
41ed70551dd7e841883ab8f0b16bf041
76b7d1480e4f0af9f3d4c3595768d068 ... Hash #3
20d2a7bc994987302e5b1ac80fc425fe
25f8b63169ea78e68fbaaefa59379bbf ... Hash #4

01 ................................. Flag bytes: 1
1d ................................. Flags: 1 0 1 1 1 0 0 0

Mercle Block Message包含，块头全部信息，交易个数，以及用于生成Merkle Proof的Hash值列表和Flag值列表。

接下来SPV可以根据交易个数得出 Merkle Tree的大小（不用真正意义上的建立一个MerkleTree，而是通过Merkle Tree 的SIZE 从而推导出 Merkle Path里节点间联系），根据Hash列表以及 Flags列表确定目标交易及它到Merkle Root的路径。
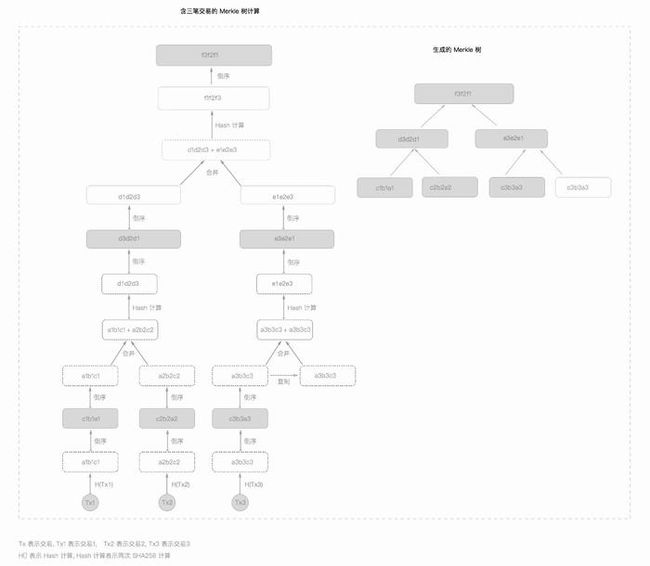
具体流程可以参考下图：

图中Flag多出的一个0是为了凑够字节于是在最后加了一个0

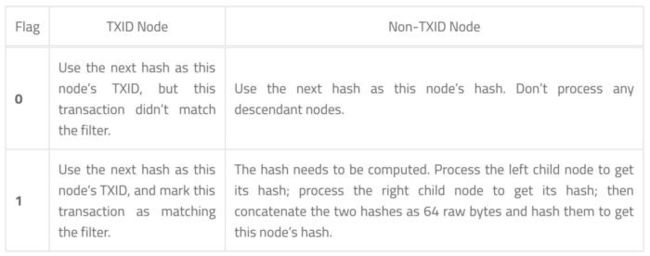
Flag操作含义：

最后如何衡量我们指定的Block都是否包含目标交易？有以下条件：

if you find a node whose left and right children both have the same hash, fail. This is related to CVE-2012-2459.

If you run out of flags or hashes before that condition is reached, fail. Then perform the following checks (order doesn’t matter):

• Fail if there are unused hashes in the hashes list.
• Fail if there are unused flag bits—except for the minimum number of bits necessary to pad up to the next full byte.
• Fail if the hash of the merkle root node is not identical to the merkle root in the block header.
• Fail if the block header is invalid. Remember to ensure that the hash of the header is less than or equal to the target threshold encoded by the nBits header field. Your program should also, of course, attempt to ensure the header belongs to the best block chain and that the user knows how many confirmations this block has.

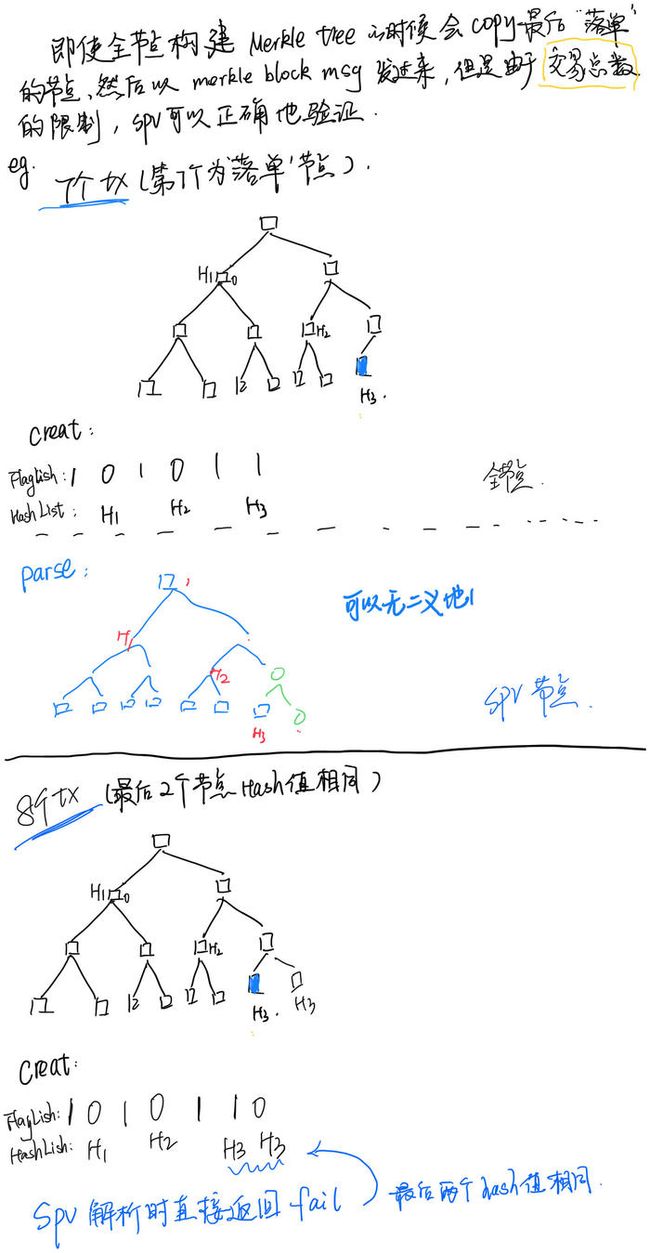
可以分成两个阶段，在构建过程中：

• 如果某个Node的左右节点的hash相同，则返回 fail；

  简单来说：为了防止重复交易设置的，spv会去检查最后两个节点的hash值是否相同，如果相同则返回错误。具体解释可以参考博士论文：on the application of hash function in bitcoin
  之前有过一个存疑点：全节点在构建merkle tree的时候，对待“落单”的节点会copy然后以MerkleBlockMessage发过来，这种情况会不会与上述的判断条件矛盾？
  回答：不会，主要原因：交易总数限制着。具体在不存在性证明部分进行解释（涉及全节点生成MerkleBlockMessage逻辑）。

• 如果在还没能得出Merkle Root的情况下，Flag或者Hash已使用完，则返回 fail。

构建完毕之后：

• 如果hash列表中还有没有使用到的hash值，返回 fail；
• 如果flag列表中还有没有使用到的flag值，返回 fail，除非为了满足最低flag个数标准从而填充的0（如上图）；
• 本地生成的Merkle root用于和块头中的Merkle root不相同，返回 fail；
• 如果块头不合法（PoW的值大于Target），返回 fail；

根据Merkle path进行存在性证明的PoC代码如下：

const HashSize = 32


func main() {
    var nodeshash []*chainhash.Hash
//[h1 h2 h3 h4 h12 h34 root]
    var hashstrings = []string{
        "8c14f0db3df150123e6f3dbbf30f8b955a8249b62ac1d1ff16284aefa3d06d87",
        "fff2525b8931402dd09222c50775608f75787bd2b87e56995a7bdd30f79702c4",
        "6359f0868171b1d194cbee1af2f16ea598ae8fad666d9b012c8ed2b79a236ec4",
        "e9a66845e05d5abc0ad04ec80f774a7e585c6e8db975962d069a522137b80c1d",
        "ccdafb73d8dcd0173d5d5c3c9a0770d0b3953db889dab99ef05b1907518cb815",
        "8e30899078ca1813be036a073bbf80b86cdddde1c96e9e9c99e9e3782df4ae49",
        "f3e94742aca4b5ef85488dc37c06c3282295ffec960994b2c0d5ac2a25a95766",
    }

     root,err := chainhash.NewHashFromStr("f3e94742aca4b5ef85488dc37c06c3282295ffec960994b2c0d5ac2a25a95766")
    if err != nil {
        fmt.Printf("wrong" )
        return
    }

    for _ , item := range hashstrings{
        hash, err := chainhash.NewHashFromStr(item)
        if err != nil {
            fmt.Printf("wrong2+%s",item )
            return
        }
        nodeshash = append(nodeshash, hash)
    }
    result := merklerootinclusive(nodeshash,2,root)

    fmt.Printf("result: %t" ,result)

}

func merklerootinclusive(nodeshash []*chainhash.Hash,index int,root *chainhash.Hash) bool{
    length := len(nodeshash)
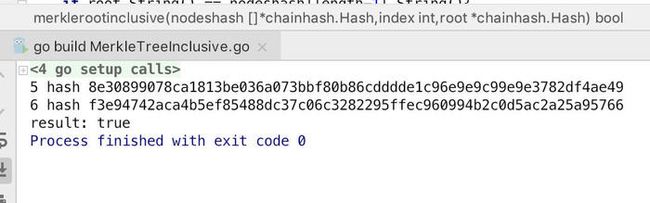
    if length

程序用例，比如查找的tx是6359f0868171b1d194cbee1af2f16ea598ae8fad666d9b012c8ed2b79a236ec4，
计算出来的ancients的hash：index为5和6的节点。其中index为6的节点即为我们算出来的merkle root节点，值与块头中的root相等，存在性证明通过。

image

Merkle Trees Exclusive Verification（Non-membership Proofs）(TODO 用图展示 IDEA)

Merkle Tree不存在性证明是最近一个热门话题，其实相关资料并没有很多。而最近提的很多是因为11月15日BCH再一次的硬分叉，这一次分叉中有一个重要内容 规范交易排序：除了coinbase交易之外，区块内的交易必须按交易 id的数字（大端表示）升序排序，在Merkle Tree中它们会被解释为256位的小端整数（little endian integers）。coinbase交易必须是一个区块当中的第一笔交易。

有了这个规范交易排序，之前一直被社区讨论的的不存在证明的方案之一：基于排序交易的不存在性证明，有望更进一步发展。

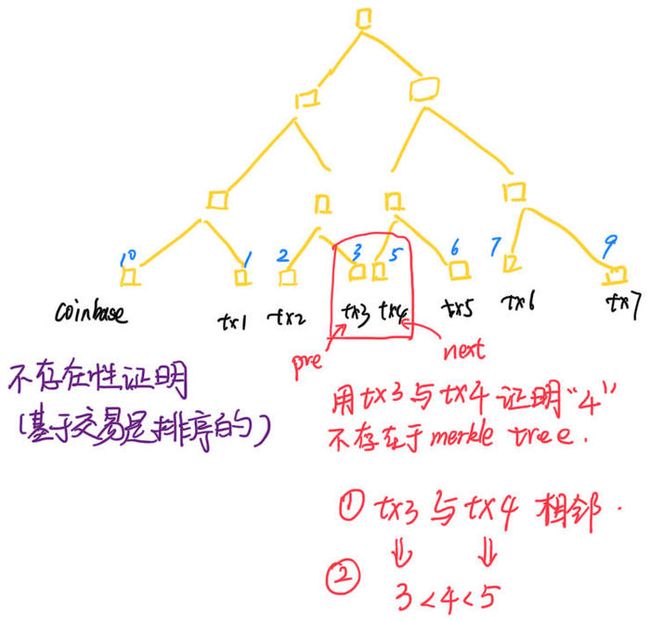
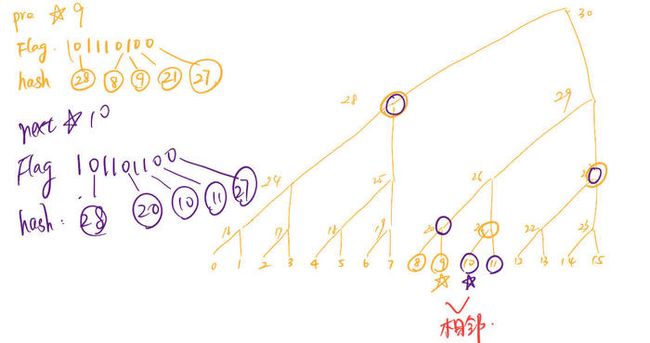
不存在性证明的意义是什么？倘若SPV请求的目标交易并不在相应的块中，全节点应该怎么证明该目标交易并不在块的交易列表中呢？如果全部交易发过去让SPV节点一个个遍历比对，对于大区块结构区块而言，这种方案效率非常低。所以基于排序交易的不存在性证明的idea是：，先让目标交易与Coinbase交易比对，如果不相等，再去与排序后的交易中比对，找到最大的小于目标交易的交易，记为pre，最小的大于目标交易的交易，记为next。通过证明pre与next在排序后交易列表里位置相邻（中间不存在其他节点），并且都可以验证其在相应的block中（即有Merkle Tree Inclusive Verifacation），从而可证明目标交易并不在block的交易列表中。

不存在性证明具体方案是本人参考github上别人的idea：Sorted merkle tree as solution to issue #693设计的：通过生成pre 与 next 节点用于存在性证明的MerkleBlock Message来实现不存在性证明。
本方案设计原因有两个：

1. 比对pre与next的MerkleBlock Message里的Merkle Root从而确定他们都在同一个块的交易列表中。
2. 在Merkle Tree Inclusive Verifacation过程中，我们不仅可以确认两者的存在性，而且可以锁定pre（或next）交易在Merkle Tree TXID Nodes中的位置，由于Merkle Tree TXID Nodes与block中交易列表的位置一一对应，根据对比pre 与 next 在同一棵Merkle Tree 中 TXID Nodes的Index可以确定pre 与 next是相邻的。

全节点生成 MerkleBlock Message的过程可以参考下图：

展示这个图也是为了证明我们确实可以通过给出MerkleBlock Message来锁定pre（或next）交易在Merkle Tree TXID Nodes中的位置。

基于排序交易的不存在性证明的PoC代码如下

const HashSize = 32

func main() {
    var nodeshash []*chainhash.Hash
    //sortedtxhash ：[coinbase tx,small ....  big]
    var hashstrings = []string{
        "a40d79679a8f2d532ece4a3fa4b382470810037ddf36814989732d65e30a926d",
        "0ba507f50b62ecfacf9c64681231bdb3ae154f9cab0bbd61abba0c6b5341a16c",
        "2cdcefb08d10d59f81401f3a492c2c8e9929088245111cc4ce6a56b5617bdad9",
        "37a99f006f115afad21a03b7d6f3568d9f3c5d487c9ccc17476baf472e17ec1d",
        "3aa5297e0318275910d82c17d6b25313e0dc73875bff3f0f2597fc2eb61ed5dd",
        "548dbb1ef032c8e1a72e7f8a56ce89c8da37aff930a6430738badef2303b5c60",
        "584bd7e5e5efcff0db5beffbdde252f60d3c4c12550a9dd15e0d03f047feea67",
        "6307ac1a59a635fcdf82953f8a55df6062eed7ebb32e189586281d352766cb17",
        "668d8d9dc1b168bf401b83a150c97d358c9fd6f43a32dd8148afc4979dbd81a4",
        "68f68945ad4bbbc1572963119ead4436ccbc33312f26fb05f61ae1673b21b103",
        "89b0b1a4d5f907d378543cee4106df480f713a54c5545232e44cc346562cbf30",
        "c76d38a803601c93bc7f07023fef7c7a151b5b7991451dbcc76201a74a240c5f",
        "cd71afaa322db432aa80031d571364548e6c4d56efb34dbde24fcc2e9b6f97bc",
        "d51ffcb68bb8b673286a9693c03f29bf8c62d23cd3ce0c0752a9b61668ca4275",
        "df24734cafbe5cf8f07749a1007ea703f0deaedf850a93ed7f7b85f5a8b3ceb3",
        "e7e011c98726aec33b9929020f279d3c716185ebd9160cee5a721a06b8225605",

    }

    targettx,err := chainhash.NewHashFromStr("6f7c8a6a2ed308074bf5078fd141e66e7d3440ec348ddd38c9ec7882f7960e64")
    if err != nil {
        fmt.Printf("wrong" )
        return
    }

    for _ , item := range hashstrings{
        hash, err := chainhash.NewHashFromStr(item)
        if err != nil {
            fmt.Printf("wrong2+%s",item )
            return
        }

        nodeshash = append(nodeshash, hash)
    }
    merklerootexclusive(nodeshash,targettx)
}


func merklerootexclusive(sortedtxhash []*chainhash.Hash,targettxhash *chainhash.Hash)  {//已确认target不在txs里，merkle树已构造出，给出不存在性证明
    length := len(sortedtxhash)
    targettxhash = reverseHash(targettxhash)

    index := 1
    slice := 0
    for  ; index < length  ; {
        cur := reverseHash(sortedtxhash[index])
        if targettxhash[slice] > cur[slice] {
            index++
            slice = 0
            continue
        }else if targettxhash[slice] == cur[slice] {
            slice ++
            continue
        }else {
            if index == 1 {
                //next = sortedtxhash[0]
                fmt.Printf("mintx : %s vs \ntarget : %s \n",reverseHash(cur).String(),reverseHash(targettxhash).String())//最小tx>目标交易
                minproof(length,1)//给出cur的proof路径及hash，并锁定cur指向最小tx
                return
            }else {
            fmt.Printf("pretx : %s <\ntargettx : %s <\nnexttx : %s \n",sortedtxhash[index-1].String(),targettxhash.String(),sortedtxhash[index])//最大tx<目标交易
            normalproof(length,index-1,index)//给出pre，next的proof路径及hash，spv根据生成的merkle路径定位可知pre与next相邻
            return
            }
        }
    }
    fmt.Printf("maxtx : %s vs \ntarget : %s \n",sortedtxhash[length-1],reverseHash(targettxhash).String())//最大tx<目标交易
    maxproof(length,length-1);//给出cur的proof路径及hash，锁定cur指向最大tx
    return


}
func minproof(txsum int , targetindex int)  {
    var flag string
    flag = buildflags(txsum,targetindex)

    fmt.Printf("minflag : %s" ,flag)
}

func maxproof(txsum int , targetindex int)  {
    var flag string
    flag = buildflags(txsum,targetindex)

    fmt.Printf("maxflag : %s" ,flag)
}

func normalproof(txsum int , preindex int, nextindex int)  {
    preflag := buildflags(txsum,preindex)
    nextflag := buildflags(txsum,nextindex)

    fmt.Printf("preflag : %s\n" ,preflag)
    fmt.Printf("nextflag : %s" ,nextflag)

}

func buildflags(txsum int , targetindex int) string {

    hash := list.New()
    nodeslength := txsum * 2-1
    var substr string
    for cur:=targetindex;cur < nodeslength-1; {
        if cur%2 == 0 {
            substr = "1"+substr+"0"
            if cur == targetindex{
                hash.PushFront(cur)
                hash.PushBack(cur + 1)
            }else {
                hash.PushBack(cur+1)
            }
        }else {
            substr = "01"+substr
            if cur == targetindex{
                hash.PushFront(cur)
                hash.PushFront(cur - 1)
            }else {
                hash.PushFront(cur-1)
            }
        }
        cur=nodeslength - (nodeslength - cur - (cur+1)%2)/2
    }
    fmt.Print("hash list of ", targetindex," :")
    for e := hash.Front(); e != nil; e = e.Next() {
        fmt.Print(" ",e.Value, ";")
    }
    fmt.Print("\n")
    //fmt.Printf("flag : %s",substr)
    return "1"+substr//root 节点

}

func reverseHash(hash *chainhash.Hash) *chainhash.Hash {

    for i := 0; i < HashSize/2; i++ {
        hash[i], hash[HashSize-1-i] = hash[HashSize-1-i], hash[i]
    }

    return hash
}

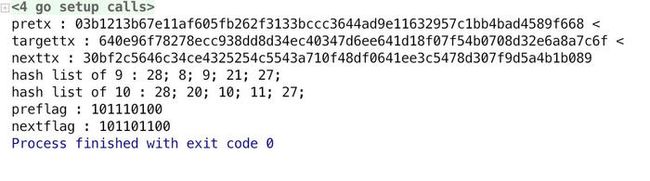
程序用例，比如查找的tx是
"6f7c8a6a2ed308074bf5078fd141e66e7d3440ec348ddd38c9ec7882f7960e64"，交易列表“hashstrings”中不存在，返回两笔相邻交易的存在性证明：
pre：“68f68945ad4bbbc1572963119ead4436ccbc33312f26fb05f61ae1673b21b103”
和
next：“89b0b1a4d5f907d378543cee4106df480f713a54c5545232e44cc346562cbf30”

图中的pre 与 next是用小端法表示的，以及Hash列表和Flag列表。Hash 列表简化成了相应Node在Merkle Tree中对应的index值。

回答之前问题：

To be Continued

其实Merkle Tree被广泛运用于区块链中，虽然在Bitcoin中是二叉树的结构，其实merkle tree也不一定是二叉树，可以是任意树结构，也可以有很多变种，比如Plasma Cash用来存储关于存储资产的信息的Sparse Merkle Tree，而在以太坊中用于存储信息的是“Merkle Patricia Tree”，等等。