梯度下降和反向传播算法讲解

一、梯度下降

1. 原理讲解

        在讲梯度下降之前，先向大家推荐一门课程《数值分析》，有的书也将它称为《计算方法》。

数值分析(numerical analysis)，为数学的一个分支，是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。它以数字计算机求解数学问题的理论和方法为研究对象，为计算数学的主体部分。

        这门课程详细得介绍了如何用计算机求解积分、微分、导数、方程根、微分方程、一元线性方程组、函数极值。那么我们今天要讲解的梯度下降方法就是《数值分析》里面的一个模块。梯度下降算法是用来求一个函数的极小值点。举个例子：

求    的函数极小值。函数图像如图：

y的图像

在数学上，求y的极小值点可以通过对y求一次导数，根据导数的零点和函数的单调性能够精确地算出极小值点地值。我们在这里手算以一下：

 ,   解出x1 = 3.270083,    x2 = -1.936750。结合函数图像可以知道极小值点是x1。

但是，计算机解决的问题是普遍性的，通用性的。这道题的y毕竟是一个普通的多项式函数，如果现在一个函数带上积分、带上三角函数，带上e，带上指数对数函数，此时人工手算的方法就远远不够了。

梯度下降方法就是通过迭代的方式，每次进一小步寻找最小值。

注意到x1的左侧A点导数值小于0，x1的右侧B点导数值大于0，x1处导数值等于0. 随机初始化一个点p，当p在点A时，p = p + δ，当p在B点时，p = p - δ，其中δ = 前进步长，也就是可以写成 p = p - 学习率 * p点导数值。当p点充分接近于x1时，可以停止迭代，那么经过迭代，极小值点就可以找出来。

公式化为：  (r是很小的一个数，表示学习率）。当然最后迭代的结果取决于选择的点的位置，当初始点p在A, B之间，则能够迭代出x1，当初始点在c附近，则无法迭代出结果，也就是说算法不会收敛，只会向左一泻千里。当然，数值分析里还有很多算法都取决于初始值的位置。

2.代码实现

说这么多，我们用代码实现一下这个算法，选用cpp语言。

#include
#include

using namespace std;

long long N;        //迭代次数
double p;           //初始位置
double r;           //学习率


double ff(double x){        // y的导数
    return 3.0 * pow(x, 2) - 4.0 * x - 19;
}


int main(){
    scanf("%lld%lf%lf",&N, &p, &r);
    for(int i = 0;i

运行一下程序，显示执行结果：

程序运行结果

N	p	r	极小值点
100	0	0.01	3.270083
100	1	0.05	3.270083
10	0	0.2	-4989812654385.430664
10	-5	0.01	-1447.283969

 

从上面的表格可以看到，当我们的参数选择的合适的时候，是可以计算出极小值点x1的，但是如果学习率过大，会出现点p在极值点处左右摇摆的情况，而不能收敛到x1。而当p被“甩”到左侧时，就会出现最后一种情况，函数永远无法收敛。当然，现在有很多方法能够有效避免这种情况，比如学习率随着迭代逐渐改变，而不使用一个固定的学习率，或者随机初始化几个点，然后找到能够收敛的点等等措施。

3. 用梯度下降求解线性回归

        线性是一个好的特性，线性回归同样也是一个最简单的回归，我们可以用手算或者某种公式就能够算出需要评估的斜率和截距。回顾用手算线性回归方法：已知, ...... , ，拟合出直线 y = ax + b。

<1,6> , <2, 8> , <3, 9.5>, <4, 11.5>, <5, 14>

首先确定距离函数L(也称为损失函数）， ，我们要寻找使L取极小值的a和b。把xi和yi看成常数，那么L可以看成关于a和b的函数，也即求L的极小值点。

我们有两种方法，一种是手算求导找到函数零点后判断极小值点，另一种方法就是使用我们的梯度下降方法。两种方法都算一遍。计算结果如图：

    

令，解出a和b即可。结果为：

  （抄百度百科的）

计算出a = 1.95, b = 3.95

用梯度下降方法计算：

回顾梯度下降公式：

那么每次迭代都小部分更新a和b，当迭代次数充分后，可以计算出a和b的数值解。

下面上代码：

#include
#include

using namespace std;

/**
    用梯度下降方法求线性回归(不是最小二乘)

    输入：N L, 表示数据结点数和训练轮次
    输出：a, b， 表示y = ax + b

**/

double a, b;          // y = ax + b
double r1, r2;      //a, b 学习率
long long N;        //顶点个数
long long L;        //迭代次数
unordered_map data;

void init(){        //初始化
    a = 0.5;        
    b = 0.5;
    r1 = r2 = 0.005;    
}

void train(){
    double na = 0, nb = 0;
    for(pair p : data){
        double xi = p.first, y_bar = p.second;
        na += (xi * (a * xi + b - y_bar));
        nb += (a * xi + b - y_bar);
    }
    a = a - (r1 * na);
    b = b - (r2 * nb);
    return;
}

int main(){
    init();
    cin>>N>>L;     

    double x, y;
    for(long long i = 0;i>x>>y;
        data[x] = y;
    }

    for(long long i = 0;i
 
  
可以看到a = 1.95， b = 3.95，计算结果和解析解一致。 
 
  
所以我们也可以用梯度下降的方法来求解线性回归（不过都能通过手算出解析解了，为啥还有梯度下降多此一举呢，手动斜眼）。
 
  
练习1：用梯度下降求解的极值点
 
  
练习2：用梯度下降求解点集{<0.5,1.455>, <1, 9.777>, <1.5, 29.224>, <2,  403.429>, <2.2, 1422.257>} 拟合中a的结果。
 
  
二、反向传播
 
  
反向传播是在神经网络中，求解参数的一个方法，其中用到了梯度下降求解极小值和函数求导的链式法则两个工具。
 
  
我们先考虑一个极简单的情况，其中神经元内不含激活函数,（也就是激活函数是y = x)：
 
  
 
 
  
 
  
已知输出结果有下面公式：
 
  
 
  
损失函数为：   
 
  
其中 
 
  
   (1)
 
  
    (2)
 
  
我们需要做的是，寻找当L最小的时候, wi,j的值。换句话说，对于函数L，其自变量为wi,j。当然采用梯度下降法。
 
  
回忆梯度下降法公式（用w1,1举例子）：
 
  
 
  
每轮迭代时，都需要计算        ，如何计算呢？这明显是一个多元函数的嵌套，求导符合链式法则。
 
  
则    ,  等式右边第一项求导后是  ， 等式第二项求导可根据(1)式进行，求导结果是xi,1。
 
  
那么二者相乘即可算出 
 
  
从上面的公式中可以看出，每轮迭代时，w1,1的更新公式是
 
  
同理， 也可以按这种方法，一步一步迭代出来。
 
  
 
 
  
考虑激活函数
 
  
令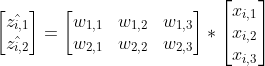 
 
  
激活函数采用sigmoid函数：
 
  
 
  
 
  
还是观察w1,1的更新公式：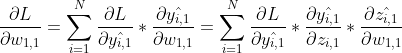 
 
  
对比原来的更新公式，其实就多了一个中间变量zi,1。
 
  
上式第一项不变，第二项是对sigmoid求导，第三项不变，最后可以整理成一个求解参数式子，即为反向传播。
 
  
为什么叫反向传播呢？
 
  
这里只是包含一层的神经网络，没法体现出反向传播的直观，但是如果是深层结构，我们更新完最内层的w后，其求导结果还可以继续使用，然后再通过内层对外层的结果，算出L对外层w的导数，实现了误差函数的结果反向传播。
 
  
 
 
  
用C++实现简单的神经网络
 
  
为了方便，采用随机梯度下降方法，同时隐藏层的激活函数采用sigmoid函数，学习率固定为0.2.
 
  
下图是首先需要的公式推导，相应的偏导数已经计算出来。
 
  
 
  
 
 
  
代码如下：
 
  
#include
#include

/**
    神经网络(2,3,2),2输入，2输出，最后一维是偏置，恒为1，激活函数采用sigmoid，输出不包含softmax

    输入：
    N    L  , N点的个数，L迭代轮次
    然后输入N个(x1,x2,y1,y2)

    然后输入测试样例

    输入如：

20 10000
0 1 1 0
1 2 1 0
1 3 1 0
-1 2 1 0
-1 3 1 0
2 10 1 0
-3 6 1 0
3 7 1 0
0 5 1 0
-1 8 1 0
0 -1 0 1
1 -2 0 1
1 -3 0 1
-1 -2 0 1
-1 -3 0 1
2 -10 0 1
3 -6 0 1
-3 -2 0 1
0 -5 0 1
2 -3 0 1

//测试样例
2 10
2 -5
0 -9
0 4


**/
using namespace std;


int N;          //顶点数
int L;          //学习轮次

double W[3][3];
double U[2][3];
double rate = 0.02;


struct elem{
    double x[3];            //
    double y[2];
};

elem data[10005];

void init(){
    for(int i = 0;i<3;i++){
        for(int j = 0;j<3;j++){
            W[i][j] = 0.5;
        }
    }

    for(int i = 0;i<3;i++){
        U[1][i] = 0.5;
        U[2][i] = 0.5;
    }
}

double h[3];        //记录前向传播的值
double z[3];
double o[3];

void train(int n){          //
    //前向传播
    for(int i = 0;i<3;i++){
        double d = 0;
        for(int j = 0;j<3;j++){
            d += W[i][j] * data[n].x[j];
        }
        h[i] = d;
    }
    for(int i = 0;i<3;i++){
        z[i] = 1.0/(1.0 +pow(exp(1.0),-h[i]));
    }

    for(int i = 0;i<2;i++){
        double d = 0;
        for(int j = 0;j<3;j++){
            d += U[i][j] * z[j];
        }
        o[i] = d;
    }

    //梯度下降更新
    double uu[3][2];        //  dL/du
    fill(uu[0], uu[0]+3 * 2, 0);

    //更新uij
    for(int i = 0;i<3;i++){
        for(int j = 0;j<2;j++){
            uu[i][j] = (o[i]-data[n].y[i]) * z[j];
            U[i][j] = U[i][j] - rate * uu[i][j];
        }
    }

    //更新wij
    double ww[3][3];    //    dL/wij
    fill(ww[0], ww[0]+3*3, 0);


    for(int i = 0;i<3;i++){
        for(int j = 0;j<3;j++){
            for(int k = 0;k<2;k++){
                double tmp = (1.0/(1.0 +pow(exp(1.0),-h[i]))) * (1-((1.0/(1.0 +pow(exp(1.0),-h[i])))));
                ww[i][j] += (o[k]-data[n].y[k])*U[k][i]*tmp*data[n].x[j];
            }
            W[i][j] = W[i][j] - rate * ww[i][j];
        }
    }
    return;
}

void printParam(){
    cout<<"W:"<>N>>L;
    for(int i = 0;i>data[i].x[0]>>data[i].x[1]>>data[i].y[0]>>data[i].y[1];
        data[i].x[2] = 1;
    }

    init();

    for(int i = 0;i>e.x[0]>>e.x[1];
        e.x[2] = 1;
        res(e);
        cout<