matlab实现主成分回归

主成分回归就是先对数据进行主成分分析，再进行多元线性回归。
主成分分析参考上篇博客，蹦篇博客介绍多元线性回归及其MATLAB实现。
多元线性回归是一种常用的线性建模方法。如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
以下是MATLAB的实现方式

a = load('C:\Users\yxz\Desktop\pca_duoyuan\data.txt');%经过PCA分析之后的主成分
U = load('C:\Users\yxz\Desktop\pca_duoyuan\U.txt');%这格式pca之前原数数据的特征向量
a2=xlsread('C:\Users\yxz\Desktop\pca_duoyuan\testjieguo.csv');%读文件，测试数据
a2=a2(:,2:513); %从第二列到最后
PCA_a2=a2*U;
x1=a(:, 1);
x2=a(:, 2);
x3=a(:, 3);
x4=a(:, 4);
x5=a(:, 5);
x6=a(:, 6);
x7=a(:, 7);
x8=a(:, 8);
y=a(:,9);
X=[ones(length(y),1), x1,x2,x3,x4,x5,x6,x7,x8];
[b,bint,r,rint,stats]=regress(y,X);
b;bint;stats;
b2=[b(2),b(3),b(4),b(5),b(6),b(7),b(8),b(9)];
rcoplot(r,rint)%残差及其置信区间作图
%b是方程的系数矩阵
%bint是回归系数的区间
%r残差
%rint置信区间
%stats用于检验回归模型是否正确,分别是R的平方，F值，概率P
% 预测
ty1=b(1)+b2*PCA_a2(1,:)';
ty2=b(1)+b2*PCA_a2(2,:)';
ty3=b(1)+b2*PCA_a2(3,:)';
ty4=b(1)+b2*PCA_a2(4,:)';
ty5=b(1)+b2*PCA_a2(5,:)';
ty6=b(1)+b2*PCA_a2(6,:)';
ty7=b(1)+b2*PCA_a2(7,:)';
ty8=b(1)+b2*PCA_a2(8,:)';
t=1:60;
figure(1);
y_fitting=X(t,:)*b;
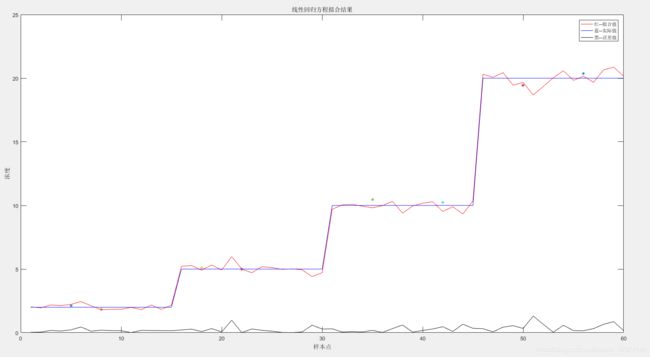
plot(t,y_fitting,'r-',t,y(t,:),'b-',t,abs(y_fitting-y(t,:)),'k-',5,ty1,'*',8,ty2,'*',18,ty3,'*',22,ty4,'*',35,ty5,'*',42,ty6,'*',50,ty7,'*',56,ty8,'*');% 绘制出Y实际值曲线t,y_fitting，和拟合值曲线Y(t,:)，以及残差曲线abs(y_fitting-Y(t,:))
legend('红--拟合值','蓝--实际值','黑--误差值');
title('线性回归方程拟合结果');
xlabel('样本点');ylabel('浓度');