飞翔的河马F

深度学习20问--知识点2（5/20）

这里写目录标题

1、权重初始化
2、归一化、标准化

归一化（MinMaxScaler）（normalization）
标准化（StandardScaler）
对比

3、PCA（principal component analysis）
4、既然cnn对图像具有平移不变性，那么利用图像平移（shift）进行数据增强来训练cnn会有效果吗？
AdaBoost
5、深度学习训练中数据规范化(Normalization)的重要性
6、霍夫曼编码
7、生成模型和判别模型的区别
8、ROC AUC

ROC曲线
AUC(Area under the ROC curve)
总结

9、模型集成的方法

一级目录

二级目录

三级目录

1、权重初始化

参考此链接，侵删

pytorch官方的init详解

1. 均匀分布

torch.nn.init.uniform_(tensor, a=0, b=1)  # 服从~U(a,b)

2. 正态分布

torch.nn.init.normal_(tensor, mean=0, std=1)   # 服从~N(mean,std)N(mean, std)N(mean,std)

3. 初始化为常数

torch.nn.init.constant_(tensor, val)  # 初始化整个矩阵为常数val

4. Xavier
基本思想是通过网络层时，输入和输出的方差相同，包括前向传播和后向传播。

初始化会出现的问题：

如果初始化值很小，那么随着层数的传递，方差就会趋于0，此时输入值也变得越来越小，在sigmoid上就是在0附近，接近于线性，失去了非线性
如果初始值很大，那么随着层数的传递，方差会迅速增加，此时输入值变得很大，而sigmoid在大输入值写倒数趋近于0，反向传播时会遇到梯度消失的问题

对于Xavier初始化方式，pytorch提供了uniform和normal两种：

torch.nn.init.xavier_uniform_(tensor, gain=1) 均匀分布 ~ U(−a,a)
torch.nn.init.xavier_normal_(tensor, gain=1) 正态分布~N(0,std)

5. kaiming (He initialization)

Xavier在tanh中表现的很好，但在Relu激活函数中表现的很差，所何凯明提出了针对于Relu的初始化方法。
在ReLU网络中，假定每一层有一半的神经元被激活，另一半为0，所以，要保持方差不变，只需要在 Xavier 的基础上再除以2，也就是说在方差推到过程中，式子左侧除以2.
针对于Relu的激活函数，基本使用He initialization，pytorch也是使用kaiming 初始化卷积层参数的

pytorch也提供了两个版本：

torch.nn.init.kaiming_uniform_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)， 均匀分布 ~ U(−bound,bound)
torch.nn.init.kaiming_normal_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’), 正态分布~ N(0,std)

两函数的参数：

a：该层后面一层的激活函数中负的斜率(默认为ReLU，此时a=0)
mode：‘fan_in’ (default) 或者 ‘fan_out’. 使用fan_in保持weights的方差在前向传播中不变；使用fan_out保持weights的方差在反向传播中不变

6. 正交初始化（Orthogonal Initialization）
主要用以解决深度网络下的梯度消失、梯度爆炸问题，在RNN中经常使用的参数初始化方法。

torch.nn.init.orthogonal_(tensor, gain=1)  # 使得tensor是正交的

7. 单位矩阵初始化

torch.nn.init.eye_(tensor) # 将二维tensor初始化为单位矩阵（the identity matrix）

8. 稀疏初始化

torch.nn.init.sparse_(tensor, sparsity, std=0.01)
- 从正态分布N～（0. std）中进行稀疏化，使每一个column有一部分为0
- sparsity- 每一个column稀疏的比例，即为0的比例

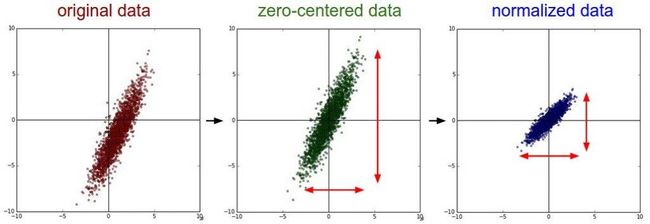
2、归一化、标准化

归一化（MinMaxScaler）（normalization）

将训练集中某一列数值特征（假设是第i列）的值缩放到0和1之间。

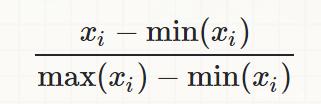
标准化（StandardScaler）

将训练集中某一列数值特征（假设是第i列）的值缩放成均值为0，方差为1的状态。如下所示：

标准化之后，数据的范围并不一定是0-1之间，数据不一定是标准正态分布，因为标准化之后数据的分布并不会改变，如果数据本身是正态分布，那进行标准化之后就是标准正态分布。

对比

进一步明确二者含义归一化和标准化的相同点都是对某个特征（column）进行缩放（scaling）而不是对某个样本的特征向量（row）进行缩放。对特征向量进行缩放是毫无意义的（暗坑1）比如三列特征：身高、体重、血压。每一条样本（row）就是三个这样的值，对这个row无论是进行标准化还是归一化都是好笑的，因为你不能将身高、体重和血压混到一起去！
在线性代数中，将一个向量除以向量的长度，也被称为标准化，不过这里的标准化是将向量变为长度为1的单位向量，它和我们这里的标准化不是一回事儿，不要搞混哦（暗坑2）。
好处
- 提升模型精度。归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。
- 提升收敛速度。对于线性model来说，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解。
在机器学习中，标准化是更常用的手段，归一化的应用场景是有限的。
- 标准化更好保持了样本间距。当样本中有异常点时，归一化有可能将正常的样本“挤”到一起去。
- 标准化更符合统计学假设对一个数值特征来说，很大可能它是服从正态分布的。
如果你不用正则，那么，标准化并不是必须的，如果你用正则，那么标准化是必须的。

3、PCA（principal component analysis）

PCA链接，侵删

只是一种总结某些数据的方法。描述一个物体有很多特征，但是其中很多属性都是相关的，因此会出现一些冗余。因此我们可以通过更少的特性总结每个物体。
PCA并没有选择一些特性然后丢弃其余。相反，它创建一些新特性，结果这些新特性能够很好地总结我们的物体。当然，这些新特性是由旧特性构建的
PCA寻找最佳的可能特性，那些可能总结红酒列表的特性中最好的那些（在所有可能的线性组合中）
PCA寻找能尽可能体现红酒差异的属性。
所以PCA寻找能够尽可能好地重建原本特性的属性。
PCA可以将数据投影到分布分散的平面内，而忽略掉分布集中的平面。

4、既然cnn对图像具有平移不变性，那么利用图像平移（shift）进行数据增强来训练cnn会有效果吗？

知乎大佬讲解，侵删

平移不变性（translation invariant）指的是CNN对于同一张图及其平移后的版本，都能输出同样的结果。
平移等价性（translation equivalence）当输入发生平移时，输出也应该相应地进行平移。
就是CNN的平移不变性主要是通过数据学习来的
结构只能带来非常弱的平移不变性
而学习又依赖于数据增强中的裁切，裁切相当于一种更好的图像平移。
全连接层更能学到平移不变性。
从单层来看，只有全局池化有一定的平移不变性，其它都比较弱甚至没有。
如果把这些层串起来，那么在使用全连接层的时候整个CNN的结构一般不具有平移不变性。
能用于分类的平移不变性主要来源于参数。因为卷积层的平移等价性，这种平移不变性主要是由最后的全连接层来学习，而对于没有全连接层的网络更难有这种性质。

AdaBoost

侵删

将多个弱分类器进行合理的结合，使其成为一个强分类器。

弱分类器：强分类器是能够正确的识别过程，弱分类器就是那个易错的。
AdaBoost算法一般是用单层决策树作为弱分类器，也就是决策树的最简化版本，只有一个决策点。也就是说对于多维特征的训练数据，这个弱分类器也只能选择其中的一个一维特征来做决策。
AdaBoost的两种权重：一种为数据权重、一种为分类器权重
- 数据权重：用于确定分类器权重（弱分类器寻找其分类最小的决策点，找到之后用这个最小的误差计算出弱分类器的权重）
- 分类器权重：说明了弱分类器在最终决策中拥有发言权的大小

5、深度学习训练中数据规范化(Normalization)的重要性

大佬链接，侵删

在pytorch附带的模型中我们可以选择预训练模型。预训练模型即模型中的权重参数都被训练好了，在构造模型后读取模型权重即可。
但是有些东西需要注意：
- 模型的权重参数是训练好的，但是要确定你输入的数据和预训练时使用的数据格式一致。
- 要注意什么时候需要格式化什么时候不需要。
平常输入的图像大部分都是三通道RGB彩色图像，数据范围大部分都是[0-255]，也就是通常意义上的24-bit图(RGB三通道各8位)。
在pytorch的官方介绍中也提到了，pytorch使用的预训练模型搭配的数据必须是：
- 3通道RGB图像(3 x H x W)
- 而且高和宽最好不低于224
- 并且图像数据大小的范围为[0-1]
- 使用mean和std去Normalize。
格式化(Normalization)
在一组图中，每个图像的像素点首先减去所有图像均值的像素点，然后再除以标准差。这样可以保证所有的图像分布都相似，也就是在训练的时候更容易收敛，也就是训练的更快更好了。
- 显然，格式化就是使数据中心对齐，如cs231n中的示例图，左边是原始数据，中间是减去mean的数据分布，右边是除以std标准差的数据分布，当然cs231n中说除以std其实可以不去执行，因为只要数据都遵循一定范围的时候（比如图像都是[0-255]）就没有必要这样做了。
这个函数强调的是把数据的方差和均值调整为1和0，具体数据落在哪个区间不重要，因为to tesor已经把数据落在0、1区间了，我试验了一下，在0、1区间内，任意调整数据，标准差是1和均值是0，最终数据都在-2~2之间。

6、霍夫曼编码

有一个例子可以看一下，侵删

霍夫曼（Huffman）编码是1952年为文本文件而建立，是一种统计zhi编码。属于无损压缩编码。
霍夫曼编码的码长是变化的，对于出现频率高的信息，编码的长度较短；而对于出现频率低的信息，编码长度较长。这样，处理全部信息的总码长一定小于实际信息的符号长度。
步骤进行：
将信号符号按概率大小进行排列.
给概率最小的两个信源符号分配一个码位0和1，然后将这两个符号合并为一个，计算其概率和作为一个新的符号进行重新排列.
重复第二步操作，直至信源只剩两个符号为止，此时两个符号的概率之后必为1. 然后依照最后一级开始，依编码路径向前返回，得到各个信源符号对应的码字.

这种编码方式实现了两个重要目标：
1.任何一个字符编码，都不是其他字符编码的前缀。
2.信息编码的总长度最小。

总结：

构建的时候创建二叉树，小概率在左，大概率在右，然后加和之后重新判断
左边分配0，右边分配1，最后从顶端读取每个字符的霍夫编码
得到的结果不是唯一的

7、生成模型和判别模型的区别

按照求解的方法，可以将分类算法分为判别模型和生成模型。给定特定的向量x与标签值y，生成模型对联合概率p(x,y)建模，判别模型对条件概率p(y|x)进行建模。
上述含义可以这么理解：生成模型对条件概率p(x|y)建模，判别模型对条件概率p(y|x)建模。前者可以用来根据标签值y生成的随机的样本数据x，而后者则根据样本特征向量x的值判断它的标签值y。
常见的生成模型有：贝叶斯分类器、高斯混合模型、隐马尔可夫模型、受限玻尔兹曼机、生成对抗网络等。
典型的判别模式有：感知机、决策树、kNN算法、人工神经网络、支持向量机、logistic回归和AdaBoost算法、最大熵模型、boosting方法、条件随机场 (conditional random field, CRF)等。

8、ROC AUC

参考链接
ROC (Receiver Operating Characteristic) 曲线和 AUC (Area Under the Curve)(Area Under theCurve) 值常被用来评价一个二值分类器 (binary classifier) 的优劣。

几乎我所知道的所有评价指标，都是建立在混淆矩阵基础上的，包括准确率、精准率、召回率、F1-score，当然也包括AUC。

ROC曲线

对于某个二分类分类器来说，输出结果标签（0还是1）往往取决于输出的概率以及预定的概率阈值。
实际上，这种阈值的选取也一定程度上反映了分类器的分类能力。我们当然希望无论选取多大的阈值，分类都能尽可能地正确，也就是希望该分类器的分类能力越强越好，一定程度上可以理解成一种鲁棒能力吧。
为了形象地衡量这种分类能力，ROC曲线横空出世
横轴：False Positive Rate（假阳率，FPR）
假阳率，简单通俗来理解就是预测为正样本但是预测错了的可能性，显然，我们不希望该指标太高。
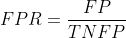
纵轴：True Positive Rate（真阳率，TPR）
真阳率，则是代表预测为正样本但是预测对了的可能性，当然，我们希望真阳率越高越好。
ROC曲线的横纵坐标都在[0,1]之间
特性
- (0,0)：假阳率和真阳率都为0，即分类器全部预测成负样本
- (0,1)：假阳率为0，真阳率为1，全部完美预测正确，happy
- (1,0)：假阳率为1，真阳率为0，全部完美预测错误，悲剧
- (1,1)：假阳率和真阳率都为1，即分类器全部预测成正样本
- TPR＝FPR，斜对角线，预测为正样本的结果一半是对的，一半是错的，代表随机分类器的预测效果
于是，我们可以得到基本的结论：ROC曲线在斜对角线以下，则表示该分类器效果差于随机分类器，反之，效果好于随机分类器，当然，我们希望ROC曲线尽量除于斜对角线以上，也就是向左上角（0,1）凸。

AUC(Area under the ROC curve)

ROC曲线一定程度上可以反映分类器的分类效果，但是不够直观，我们希望有这么一个指标，如果这个指标越大越好，越小越差，于是，就有了AUC。AUC实际上就是ROC曲线下的面积。AUC直观地反映了ROC曲线表达的分类能力。

AUC ＝ 1，代表完美分类器
0.5 < AUC < 1，优于随机分类器
0 < AUC < 0.5，差于随机分类器

总结

ROC曲线反映了分类器的分类能力，结合考虑了分类器输出概率的准确性
AUC量化了ROC曲线的分类能力，越大分类效果越好，输出概率越合理
AUC常用作CTR的离线评价，AUC越大，CTR的排序能力越强

9、模型集成的方法

转自该网站，侵删
这个比较简单，侵删
集成学习：
集成学习是一种机器学习范式。在集成学习中，我们会训练多个模型（通常称为「弱学习器」）解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确和/或更鲁棒的模型。

集成方法的思想是通过将这些弱学习器的偏置和/或方差结合起来，从而创建一个「强学习器」（或「集成模型」），从而获得更好的性能。

在集成学习理论中，我们将弱学习器（或基础模型）称为「模型」，这些模型可用作设计更复杂模型的构件。在大多数情况下**，这些基本模型本身的性能并不是非常好，这要么是因为它们具有较高的偏置（例如，低自由度模型），要么是因为他们的方差太大导致鲁棒性不强（例如，高自由度模型）。**