近年NOIP普及组复赛题目的简单讲解

NOIP2015普及组复赛

整套题都出得不错，难度适中，层次分明

建议同学们在做题的时候还是先在草稿纸上分析，把关键算法的伪代码写出来，然后设计数据进行静态查错，没有问题后再到电脑上敲出代码。实际效率会高一些，也不容易出错，除非是你对这道题太熟悉了，不需要分析就可以过的可以例外（当然每个人还是根据自己的具体情况而定，只是建议尝试一下）。

第一题 金币

感觉这道题出得不错，普及组第一题就应该是这样的

简单模拟，有一个小判断就可以了

设计数据时要考虑边界，比如本题的1，10000，其他还应考虑能够手工验算的，比如7，5组数据验证一下应该就没问题了

#include
using namespace std;
int main(){
	int k,n,d,s;
	n=d=s=0;
	cin>>k;
	do{
		n++;
		d+=n;
		if(d<=k) s+=n*n;//根据题目描述进行累加
		else s+=(k-(d-n))*n;//d>k说明最后一次不足n天，计算一下天数来乘n即可
	}while(d

第二题 扫雷游戏

穷举整个雷区每一个元素周边的地雷情况就可以了

用dx，dy这样的增量数组写起来比较简洁，这个看每个人自己的习惯了

设计数据可以考虑全*，全？，边界值n，m为1的情况，100的情况需要设计随机数据代码来生成，有时间的话也可以考虑

#include
#define N 105
using namespace std;
char a[N][N];
int b[N][N],dx[]={-1,1,0,0,-1,-1,1,1},dy[]={0,0,-1,1,-1,1,-1,1};
int main(){
	int i,j,k,n,m,x,y;
	cin>>n>>m;
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			cin>>a[i][j];
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			if(a[i][j]!='*')
				for(k=0;k<8;k++){
					x=i+dx[k];
					y=j+dy[k];
					if(x>0&&x<=n&&y>0&&y<=m&&a[x][y]=='*')
						b[i][j]++;
				}
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++)
			if(a[i][j]=='*')cout<<'*';
			else cout<

第三题 求和

这道题就有一定难度了，需要通过仔细的分析来找出规律，比较费时间

给出的数据也比较明确，也在引导你一步一步去进行深入思考

20分的数据，n<=100，和百钱百鸡相似，可以三重循环穷举

40分的数据，n<=3000，三重循环超时，可以只穷举x和z，用双重循环拿到40分，题目中也可以看到x和z的奇偶性必须是一致的，所以还可以优化一点儿

本题涉及到的数据比较大，所以在读数的时候考虑用scanf或者比scanf更优化的读入数据的方法，没准儿会多过一个点

#include
#include
#include
#define N 100005
#define M 10007
using namespace std;
int number[N],color[N];
int main(){
	int i,n,m,x,z;
	long long s=0;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
		scanf("%d",number+i);
	for(i=1;i<=n;i++)
		scanf("%d",color+i);
	for(x=1;x

60分及100分的数据，n<=100000，双重循环超时，只有考虑O(n)或nlogn算法，

可以对某种颜色的奇数或偶数部分进行分析，找出其中规律

如果不能完全判定自己找出的规律完全正确，建议将40分的程序做个函数包，处理n<=3000的情况，同时可以作为验算找规律的代码正确性的依据。

用某种颜色在奇数或偶数情况下有4个数的情况下做分析，k个数也同理可证

x   x1    x2   x3  

 color=1 有4个编号  x1 x2 x3 x4 ax1 ax2 ax3 ax4
(x1+x2)(ax1+ax2) (x1+x3)(ax1+ax3) (x1+x4)(ax1+ax4)
(x2+x3)(ax2+ax3) (x2+x4)(ax2+ax4) 
(x3+x4)(ax3+ax4)
x1*ax1+x1*ax2+x1*ax1+x1*ax3+x1*ax1+x1*ax4
x1*ax1*(k-2) + x1*(ax1+ax2+ax3+ax4+axk)=x1*(ax1*(k-2)+(ax1+ax2+...+axk))
x2*(ax2*(k-2)+(ax1+ax2+...+axk)) ... xk*(axk*(k-2)+(ax1+ax2+...+axk))

k个数的时候就是 x1*(ax1*(k-2)+(k个格子上数的和)）+...+ xk(axk*(k-2)+(k个格子上数的和）)

#include
#include
#include
#define N 100005
#define M 10007
using namespace std;
int a[N],c[N];
long long s[N][2],k[N][2],ans;
int main(){
	int i,n,m;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
		scanf("%d",a+i);
	for(i=1;i<=n;i++){
		scanf("%d",c+i);
		s[c[i]][i%2]++;//某种颜色下奇数、偶数的可以组成三元组的格子数量
		k[c[i]][i%2]=(k[c[i]][i%2]+a[i])%M;//累加该种情况下的格子上的数字和
	}	
	for(i=1;i<=n;i++)
		if(s[c[i]][i%2]>1)
			ans=(ans+i*(a[i]*(s[c[i]][i%2]-2)%M+k[c[i]][i%2]))%M;//列举计算结果
	printf("%lld",ans);
	return 0;
}

求模运算容易出错

需要设计结果超出10007的

https://blog.csdn.net/deaidai/article/details/76474018?utm_source=blogxgwz2

第四题 推销员

算法众多，数学强的可以写出好简洁的贪心算法，佩服牛人

 

NOIP2014 普及组复赛

1. 珠心算测验(count.cpp/c/pas)

【问题描述】

珠心算是一种通过在脑中模拟算盘变化来完成快速运算的一种计算技术。珠心算训练，既能够开发智力，又能够为日常生活带来很多便利，因而在很多学校得到普及。

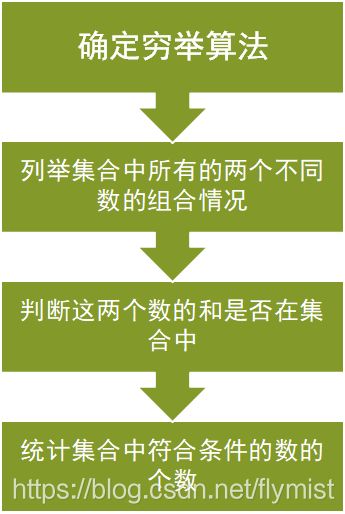
某学校的珠心算老师采用一种快速考察珠心算加法能力的测验方法。他随机生成一个正整数集合，集合中的数各不相同，然后要求学生回答：

其中有多少个数，恰好等于集合中另外两个（不同的）数之和？

最近老师出了一些测验题，请你帮忙求出答案。

【输入】

输入文件名为 count.in。

输入共两行，第一行包含一个整数 n，表示测试题中给出的正整数个数。

第二行有 n 个正整数，每两个正整数之间用一个空格隔开，表示测试题中给出的正整数。

【输出】

输出文件名为 count.out。

输出共一行，包含一个整数，表示测验题答案。

【输入输出样例】  

count.in	count.out
4 1 2 3 4	2

【样例说明】

由 1+2=3，1+3=4，故满足测试要求的答案为 2。注意，加数和被加数必须是集合中的两个不同的数。

【数据说明】

对于 100%的数据，3 ≤ n ≤ 100，测验题给出的正整数大小不超过 10,000。

简单解析：

这道题出错的同学不少，关键就是没有仔细看题目描述中的红色部分，理解出错

枚举：C(n,2)，n个数的两两不同数的组合情况

int n,i,j,k,a[105],b[105],s=0;
      memset(b,0,sizeof(b));
      cin>>n;
      for(i=1;i<=n;i++)cin>>a[i];
      for(i=1;i

如果变成双重循环的话

 int n,i,j,k,a[105],b[20005],s=0;//此处有同学设为b[105]，造成下标越界
      memset(b,0,sizeof(b));
      cin>>n;
      for(i=1;i<=n;i++)cin>>a[i];
      for(i=1;i

2.比例简化（ratio.cpp/c/pas）

【问题描述】在社交媒体上，经常会看到针对某一个观点同意与否的民意调查以及结果。例如，对某一观点表示支持的有 1498 人，反对的有 902 人，那么赞同与反对的比例可以简单的记为

1498:902。

不过，如果把调查结果就以这种方式呈现出来，大多数人肯定不会满意。因为这个比例的数值太大，难以一眼看出它们的关系。对于上面这个例子，如果把比例记为 5:3，虽然与真实结果有一定的误差，但依然能够较为准确地反映调查结果，同时也显得比较直观。

现给出支持人数 A，反对人数 B，以及一个上限 L，请你将 A 比 B 化简为 A’ 比 B’，要求在 A’和 B’ 均不大于 L 且 A’ 和 B’ 互质（两个整数的最大公约数是 1）的前提下，

A’ / B’ ≥ A / B且 A’ / B’ – A / B 的值尽可能小。

 【输入】输入文件名为 ratio.in。

输入共一行，包含三个整数 A，B，L，每两个整数之间用一个空格隔开，分别表示支持人数、反对人数以及上限。

【输出】输出文件名为 ratio.out。

输出共一行，包含两个整数 A’，B’，中间用一个空格隔开，表示化简后的比例。

【输入输出样例】  

ratio.in	ratio.out
1498 902 10	5 3

【数据说明】

对于 100%的数据，1 ≤ A ≤ 1,000,000，1 ≤ B ≤ 1,000,000，1 ≤ L ≤ 100，A/B ≤ L。

int Gcd(int a,int b){
  if(b==0) return a;
  return Gcd(b,a%b);
}
int main(){
    int A,B,L,A1,B1,t,i,j;
	double f,f1,m;
	cin>>A>>B>>L;
	m=L;
	f=double(A)/B;
	for(i=1;i<=L;i++)
    	  for(j=1;j<=L;j++){
            f1=double(i)/j;
    	    if( f1>=f && f1-f

3. 螺旋矩阵(matrix.cpp/c/pas)

【问题描述】一个 n 行 n 列的螺旋矩阵可由如下方法生成：

从矩阵的左上角（第 1 行第 1 列）出发，初始时向右移动；如果前方是未曾经过的格子，则继续前进，否则右转；重复上述操作直至经过矩阵中所有格子。根据经过顺序，在格子中依次填入 1, 2, 3, ... , n*n，便构成了一个螺旋矩阵。下图是一个 n = 4 时的螺旋矩阵。

1	2	3	4
12	13	14	5
11	16	15	6
10	9	8	7

现给出矩阵大小 n 以及 i 和 j，求该矩阵中第 i 行第 j 列的数是多少。

 【输入】输入文件名为 matrix.in。

输入共一行，包含三个整数 n，i，j，每两个整数之间用一个空格隔开，分别表示矩阵大小、待求的数所在的行号和列号。

【输出】输出文件名为 matrix.out。

输出共一行，包含一个整数，表示相应矩阵中第 i 行第 j 列的数。

【输入输出样例】  

matrix.in	matrix.out
4 2 3	14

【数据说明】

对于 50%的数据，1 ≤ n ≤ 100;

对于 100%的数据，1 ≤ n ≤ 30,000，1 ≤ i ≤ n，1 ≤ j ≤ n。

1	2	3	4	5
16	17	18	19	6
15	24	25	20	7
14	23	22	21	8
13	12	11	10	9

int a[5500][5500];
int main(){
	memset(a,0,sizeof(a));
	int n,t,i,j,x,y,x1,y1;
	cin>>n>>x1>>y1;
	x=0;y=0;
	t=a[x][y]=1;
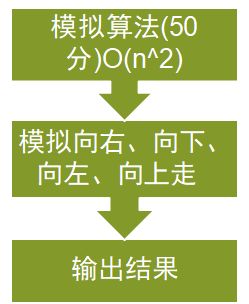
	while(t=0&&!a[x][y-1])a[x][--y]=++t;//向左
        while(x-1>=0&&!a[x-1][y])a[--x][y]=++t;//向上
	}
	cout<

不管是空间还是时间，都只能支持到5000多，n>10000的时候都会出问题

数学方法处理如下：

 

1	2	3	4	5	6
20	21	22	23	24	7
19	32	33	34	25	8
18	31	36	35	26	9
17	30	29	28	27	10
16	15	14	13	12	11

int n,i,j,k,x,y,f,c,s=0;
int main(){
  cin>>n>>i>>j;
  x=i;
  y=j;
  c=n;
  if(x>n/2) x=n-x+1;
  if(y>n/2) y=n-y+1;
  if(x>y) x=y;
  for(k=1;k

4. 子矩阵(submatrix.cpp/c/pas)

【问题描述】给出如下定义：

1. 子矩阵：从一个矩阵当中选取某些行和某些列交叉位置所组成的新矩阵（保持行与列的相对顺序）被称为原矩阵的一个子矩阵。

例如，下面左图中选取第 2、4 行和第 2、4、5 列交叉位置的元素得到一个 2*3 的子矩阵如右图所示。

9	3	3	3	9
9	4	8	7	4
1	7	4	6	6
6	8	5	6	9
7	4	5	6	1

的其中一个 2*3 的子矩阵是

4	7	4
8	6	9

2. 相邻的元素：矩阵中的某个元素与其上下左右四个元素（如果存在的话）是相邻的。

3. 矩阵的分值：矩阵中每一对相邻元素之差的绝对值之和。

 本题任务：给定一个 n 行 m 列的正整数矩阵，请你从这个矩阵中选出一个 r 行 c 列的子矩阵，使得这个子矩阵的分值最小，并输出这个分值。

【输入】输入文件名为 submatrix.in。

第一行包含用空格隔开的四个整数 n，m，r，c，意义如问题描述中所述，每两个整数之间用一个空格隔开。

接下来的 n 行，每行包含 m 个用空格隔开的整数，用来表示问题描述中那个 n 行 m 列的矩阵。

【输出】输出文件名为 submatrix.out。

输出共 1 行，包含 1 个整数，表示满足题目描述的子矩阵的最小分值。

【输入输出样例 1】

submatrix.in	submatrix.out
5 5 2 3 9 3 3 3 9 9 4 8 7 4 1 7 4 6 6 6 8 5 6 9 7 4 5 6 1	6

【输入输出样例 1 说明】

该矩阵中分值最小的 2 行 3 列的子矩阵由原矩阵第4、5行与第1、3、4列交叉位置的元素组成,为

6  5  6

7  5  6, 其分值为| 6−5| + |5−6| +| 7−5| +| 5−6 |+|6 − 7| +| 5 − 5| +| 6 − 6| = 6。

【输入输出样例 2】

submatrix.in	submatrix.out
7  7 3 3 7  7 7 6 2 10 5 5  8 8 2 1  6 2 2  9 5 5 6  1 7 7  9 3 6 1  7 8 1  9 1 4 7  8 8 10 5 9 1 1  8 10 1  3 1 5 4  8 6	16

【输入输出样例 2 说明】

该矩阵中分值最小的 3 行 3 列的子矩阵由原矩阵的第 4 行、第 5 行、第 6 行与第 2 列、第 6 列、第 7 列交叉位置的元素组成，选取的分值最小的子矩阵为

9  7   8

9  8   8

5  8  10

其分值为| 9−7| + |7−8| +| 9−8| +| 8−8 |+|5 − 8| +| 8 − 10| +| 9 − 9|+ | 9 − 9|+ | 8 − 7|+ | 8− 8|+ | 9 − 5|+ | 8− 8|+ | 10 − 8|= 16。

【数据说明】

对于 50%的数据，1 ≤ n ≤ 12, 1 ≤ m ≤ 12, 矩阵中的每个元素 1 ≤ a i j ≤20；

对于 100%的数据，1 ≤ n ≤ 16, 1 ≤ m ≤ 16, 矩阵中的每个元素 1 ≤ a i j ≤1000, 1 ≤ r ≤ n, 1 ≤ c ≤ m。

乘法原理，先行、后列，形成一个子矩阵。

n行中取r行的组合，n为12，最大值为?（12，6）=924，列同样如此，穷举次数为924*924=853776，不会超时；n为16时，子矩阵数量最大为=12870*12870，穷举超时

可以分情况处理：

cin>>n;

if ( n<13 )  p1();

else  p2();

穷举行

int row[55],n,r,c,m;
void dfs(int k){
  if(k>r){
    for(int i=1;i<=r;i++) cout<>n>>m>>r>>c;
  dfs(1);
  return 0;
}

穷举列的方法与之相同

穷举法(50分)

Dfs（深度优先搜索）是穷举组合中的每一种方案数的最简便的方法了。

大家可以回忆一下提高组初赛试题中看程序写结果中的第2题，Dfs穷举组合是与之类似的递归调用。

int n,m,r,c,s,Min=0x7fffffff,a[21][21],b[21][21],row[21],col[21];
void s_m ( ){
  int i,j;
  s=0;
  for(i=1;i<=r;i++)
    for(j=1;j<=c;j++){
        if(i+1<=r) s+=abs(b[i][j]-b[i+1][j]);
        if(j+1<=c) s+=abs(b[i][j]-b[i][j+1]);
    }
}
void dfs(int y){
  int i,j,k;
  if(  y > r ){
     for(j=1;j<=r;j++)
        for(k=1;k<=c;k++)  b[j][k]=a[row[j]][col[k]];
     s_m( );  
     if ( s c)
   { row[0]= 0;  dfs(1); return ; }
 for( i=col [x-1]+1; i<=m; i++)
    { col[x]=i;  DFS(x+1); }
}
int main(){
    int i,j;
    cin>>n>>m>>r>>c;
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)  
            cin>>a[i][j];
    col[0]=0;  
    DFS(1);
    cout<

要应对n>12的情况，可以进行一些预处理，用dp的方法来处理。

#define For ( i, x, y )  for ( int  i=x; i<=y; i++)
int n,m,r,c,Min=0x7fffffff,a[20][20],f[20][20],s_col[20][20],col[20],s_row[20];
int main(){
    cin>>n>>m>>r>>c;
    For ( i,1,n )
        For ( j,1,m )  cin>>a[i][j];
    col[0] = 0;
    dfs ( 1 ) ;
    cout << Min;
    return 0;
}

void dfs ( int x ) { //穷举m列上取c列的全部组合 
     if ( x > c )  dp( );
     else
        For ( i, col[x-1]+1, m ) {
           col[x] = i;
           dfs (x+1);
       }
}

inline void dp(){
    memset(f,127,sizeof(f));  memset(s_col,0,sizeof(s_col));          
    memset(s_row,0,sizeof(s_row));
    For( i,1,n )
        For( j,2,c ) // s_row[i]存储每行上c列数据相邻元素的差值和 
           s_row [ i ] + = abs( a[ i ] [ col[ j ] ] - a[ i ] [ col[ j-1 ] ]);
   For( i,1,n-1 ) // s_col[i][j]存储c列上i,j 两行数据相邻元素的差值和 
      For( j,i+1,n )
         For( k,1,c )
            s_col[i][j] + = abs( a[i][col[k]] - a[j][col[k]]);
    For( i,1,n )  // f数组的初值赋为s_row[i] 
        f [ i ] [ 1 ] = s_row [ i ] ;
    For( i,2,n ) // f[i][j]表示含第i行的j行c列子矩阵的最小分值
       For( j,2,r ){
          For( k,j-1,i-1 )
             f[ i ][ j ] = min( f[ i ][ j ] , f [ k ][ j-1 ] + s_col [ k ][ i ]);
          f[ i ][ j ] + = s_row[ i ];
       }
    For( i,r,n )
       Min = min ( Min, f[ i ][ r ] ); 
}

 

NOIP2012普及复赛

1.质因数分解

(prime.cpp/c/pas)

【问题描述】

已知正整数 n 是两个不同的质数的乘积，试求出较大的那个质数。

【输入】

输入文件名为 prime.in。

输入只有一行，包含一个正整数 n。

【输出】

输出文件名为 prime.out。

输出只有一行，包含一个正整数 p，即较大的那个质数。

【输入输出样例】

prime.in                            prime.out

21                              7

【数据范围】

对于 60%的数据，6 ≤ n ≤ 1000。

对于 100%的数据，6 ≤ n ≤ 2*10^9。

第一题较为简单，也没有陷阱，挺温柔的

int main(){
	int i,n;
	cin>>n;
	for(i=2;i<=sqrt(n);i++)
		if(n%i==0){
			cout<

2．寻宝

(treasure.cpp/c/pas)

【问题描述】

传说很遥远的藏宝楼顶层藏着诱人的宝藏。小明历尽千辛万苦终于找到传说中的这个藏宝楼，藏宝楼的门口竖着一个木板，上面写有几个大字：寻宝说明书。

说明书的内容如下：

藏宝楼共有 N+1 层，最上面一层是顶层，顶层有一个房间里面藏着宝藏。除了顶层外，藏宝楼另有 N 层，每层 M 个房间，这 M 个房间围成一圈并按逆时针方向依次编号为 0，…，M-1。其中一些房间有通往上一层的楼梯，每层楼的楼梯设计可能不同。每个房间里有一个指示牌，指示牌上有一个数字 x，表示从这个房间开始按逆时针方向选择第 x 个有楼梯的房间（假定该房间的编号为 k），从该房间上楼，上楼后到达上一层的 k 号房间。比如当前房间的指示牌上写着 2，则按逆时针方向开始尝试，找到第 2 个有楼梯的房间，从该房间上楼。

如果当前房间本身就有楼梯通向上层，该房间作为第一个有楼梯的房间。

寻宝说明书的最后用红色大号字体写着：“寻宝须知：帮助你找到每层上楼房间的指示牌上的数字（即每层第一个进入的房间内指示牌上的数字）总和为打开宝箱的密钥”。

请帮助小明算出这个打开宝箱的密钥。

【输入】

输入文件为 treasure.in。

第一行 2 个整数 N 和 M，之间用一个空格隔开。N 表示除了顶层外藏宝楼共 N 层楼，M 表示除顶层外每层楼有 M 个房间。

接下来 N*M  行，每行两个整数，之间用一个空格隔开，每行描述一个房间内的情况，其中第(i-1)*M+j 行表示第 i 层 j-1 号房间的情况（i=1, 2, …, N；j=1, 2, … ,M）。第一个整数表示该房间是否有楼梯通往上一层（0 表示没有，1 表示有），第二个整数表示指示牌上的数字。注意，从 j 号房间的楼梯爬到上一层到达的房间一定也是 j 号房间。

最后一行，一个整数，表示小明从藏宝楼底层的几号房间进入开始寻宝（注：房间编号从 0 开始）。

【输出】

输出文件名为 treasure.out。

输出只有一行，一个整数，表示打开宝箱的密钥，这个数可能会很大，请输出对 20123取模的结果即可。

【输入输出样例】

treasure.in

2 3

1 2

0 3

1 4

0 1

1 5

1 2

1

treasure.out

5

【输入输出样例说明】

第一层：

0 号房间，有楼梯通往上层，指示牌上的数字是 2；

1 号房间，无楼梯通往上层，指示牌上的数字是 3；

2 号房间，有楼梯通往上层，指示牌上的数字是 4；

第二层：

0 号房间，无楼梯通往上层，指示牌上的数字是 1；

1 号房间，有楼梯通往上层，指示牌上的数字是 5；

2 号房间，有楼梯通往上层，指示牌上的数字是 2；

小明首先进入第一层（底层）的 1 号房间，记下指示牌上的数字为 3，然后从这个房间开始，沿逆时针方向选择第 3 个有楼梯的房间 2 号房间进入，上楼后到达第二层的 2 号房间，记下指示牌上的数字为 2，由于当前房间本身有楼梯通向上层，该房间作为第一个有楼梯的房间。因此，此时沿逆时针方向选择第 2 个有楼梯的房间即为 1 号房间，进入后上楼梯到达顶层。这时把上述记下的指示牌上的数字加起来，即 3+2=5，所以打开宝箱的密钥就是 5。

【数据范围】

对于 50%数据，有 0，0；

对于 100%数据，有 0，0，0。

 

3．摆花 (flower.cpp/c/pas)

【问题描述】

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 m 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 n 种花，从 1 到 n 标号。为了在门口展出更多种花，规定第 i 种花不能超过 ai盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

【输入】

输入文件 flower.in，共 2 行。

第一行包含两个正整数 n 和 m，中间用一个空格隔开。

第二行有 n 个整数，每两个整数之间用一个空格隔开，依次表示 a1、a2、……an。

【输出】

输出文件名为 flower.out。

输出只有一行，一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 1000007 取模的结果。

【输入输出样例 1】

flower.in

2 4

3 2

flower.out

2

【输入输出样例说明】

有 2 种摆花的方案，分别是(1，1，1，2)，  (1，1，2，2)。括号里的 1 和 2 表示两种花，比如第一个方案是前三个位置摆第一种花，第四个位置摆第二种花。

【数据范围】

对于 20%数据，有  0，0，0≤ai≤8；

对于 50%数据，有 0，0，0≤ai≤20；

对于 100%数据，有 0，0，0≤ ai≤100。

 

4．文化之旅 (culture.cpp/c/pas)

【问题描述】

有一位使者要游历各国，他每到一个国家，都能学到一种文化，但他不愿意学习任何一种文化超过一次（即如果他学习了某种文化，则他就不能到达其他有这种文化的国家）。不同的国家可能有相同的文化。不同文化的国家对其他文化的看法不同，有些文化会排斥外来文化（即如果他学习了某种文化，则他不能到达排斥这种文化的其他国家）。

现给定各个国家间的地理关系，各个国家的文化，每种文化对其他文化的看法，以及这位使者游历的起点和终点（在起点和终点也会学习当地的文化），国家间的道路距离，试求从起点到终点最少需走多少路。

【输入】

输入文件 culture.in。

第一行为五个整数 N，K，M，S，T，每两个整数之间用一个空格隔开，依次代表国家个数（国家编号为 1 到 N），文化种数（文化编号为 1 到 K），道路的条数，以及起点和终点的编号（保证 S 不等于 T）；

第二行为 N个整数，每两个整数之间用一个空格隔开，其中第 i 个数 Ci，表示国家 i 的文化为 Ci。

接下来的 K 行，每行 K 个整数，每两个整数之间用一个空格隔开，记第 i 行的第 j 个数为 aij，aij= 1 表示文化 i 排斥外来文化 j（i 等于 j 时表示排斥相同文化的外来人），aij= 0 表示不排斥（注意 i 排斥 j 并不保证 j 一定也排斥 i）。

接下来的 M 行，每行三个整数 u，v，d，每两个整数之间用一个空格隔开，表示国家 u与国家 v 有一条距离为 d 的可双向通行的道路（保证 u 不等于 v，两个国家之间可能有多条道路）。

【输出】

输出文件名为 culture.out。

输出只有一行，一个整数，表示使者从起点国家到达终点国家最少需要走的距离数（如果无解则输出-1）。

【输入输出样例 1】

culture.in

2 2 1 1 2

1 2

0 1

1 0

1 2 10

culture.out

-1

【输入输出样例说明】

由于到国家 2 必须要经过国家 1，而国家 2 的文明却排斥国家 1 的文明，所以不可能到达国家 2。

【输入输出样例 2】

culture.in

2 2 1 1 2

1 2

0 1

0 0

1 2 10

culture.out

10

【输入输出样例说明】

路线为 1 -> 2。

【数据范围】

对于 20%的数据，有 2≤N≤8，K≤5；

对于 30%的数据，有 2≤N≤10，K≤5；

对于 50%的数据，有 2≤N≤20，K≤8；

对于 70%的数据，有 2≤N≤100，K≤10；

对于 100%的数据，有 2≤N≤100，1≤K≤100，1≤M≤N2，1≤ki≤K，1≤u, v≤N，1≤d≤1000，S≠T，1 ≤S, T≤N。