滑动窗口 单调队列算法解释及应用/c++/

滑动窗口

                    ---出自南昌理工学院ACM集训队

滑动窗口 可以用于处理一个数组或字符串的子区间问题
滑动窗口一般还会配合单调队列或单调栈使用。单调队列写在了后面，都是简单高效的算法。

算法详解

给你一个长度为n的数组，要你求出连续的k个值的和的最大值。
例如：

[1,3,−1,−3,5,3,6,7]       k=3

而滑动窗口的算法思想很好理解，正如其名，想象有一个长度为k的窗口，在数组从左向右滑动，每滑动一个单位，都要加上右边的一个数同时再减去左边超出窗口的数。这就是滑动窗口的基本思想了。
别看它思想简单，它的速度也很快，是线性的O(n) 。可以将嵌套循环的问题简化为单次循环！！

[1,3,-1]                   sum=3
  [3,-1,-3]                sum=-1
    [-1,-3,5]              sum=1
       [-3,5,3]            sum=5
          [5,3,6]          sum=14
            [3,6,7]        sum=16

正如这样 加上一个新的元素 再减去一个超出窗口的元素 一加一减 就是这么简单！
理解了原理 代码应该也很好写出来了吧。

#include      //万能头
using namespace std;
const int N=100005;  
int a[N];

int hdwindow(int n,int k)
{
    int ans=0,sum=0;
    for(int i=1;i<=n;i++)
    {
        if(i-k>=1) 
            sum-=a[i-k];  //减去超出窗口的元素
        sum+=a[i];  //加上新添加的元素
        ans=max(ans,sum);  //更新答案
    }
    return ans;
}
int main()
{
    int n,k,ans;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    ans=hdwindow(n,k);
    printf("%d\n",ans);
    return 0;
}

动画演示

该部分动画盗图 参考自链接: 五分钟学算法.
再比如：
给你一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

输入: "abcabcbb"
输出: 3 

与上个例子不同的是，这个窗口的大小并不是规定好的。可以想象是一个可以拉伸的窗口。

• 如果下一个要加进来的字符还没有出现在该窗口中，就把这个窗口右端增大一格，把这个元素加进来。
• 如果下一个字符已经在这个窗口出现了，那就把窗口的左端挪到上一次出现该字符的下一个位置，再将窗口右端增大一格，把这个新的元素加进来。

在一次次更新中更新窗口的最大长度，也就是最大不重复子串的长度了。
动画演示如下：

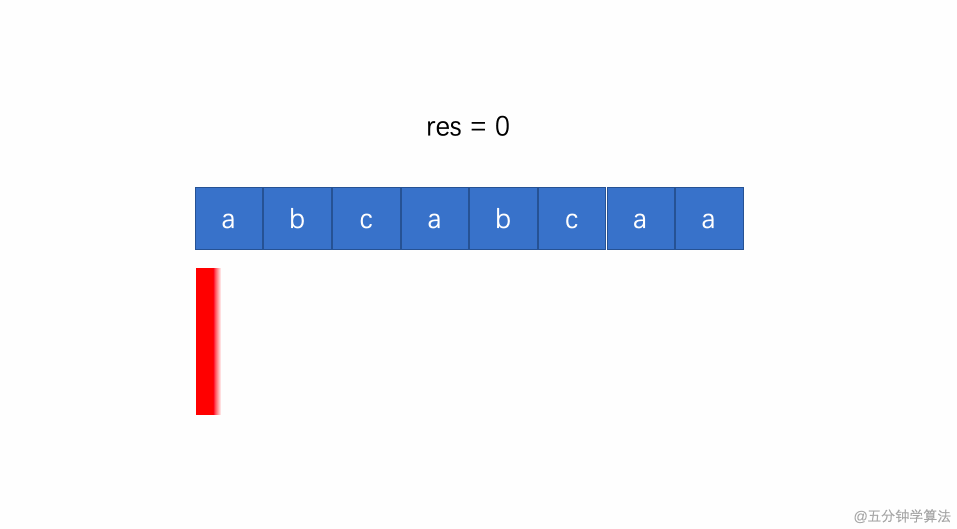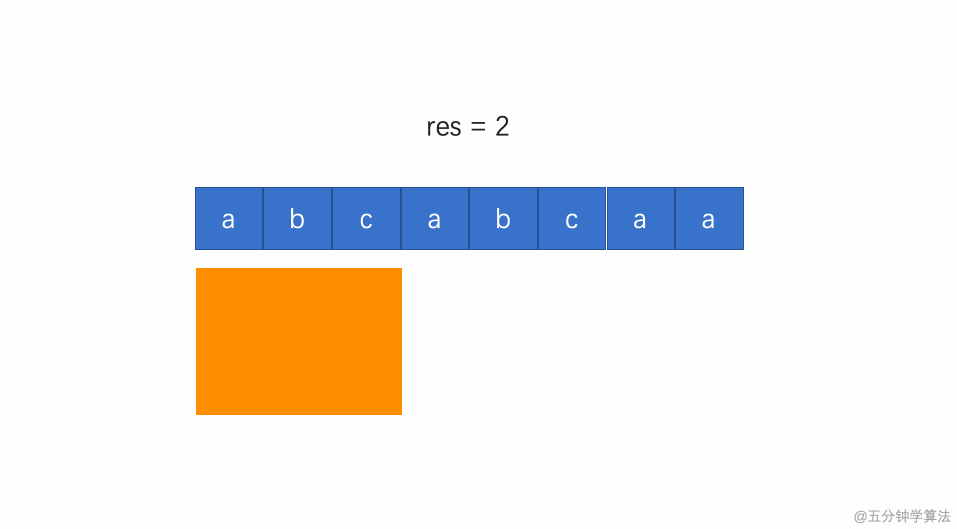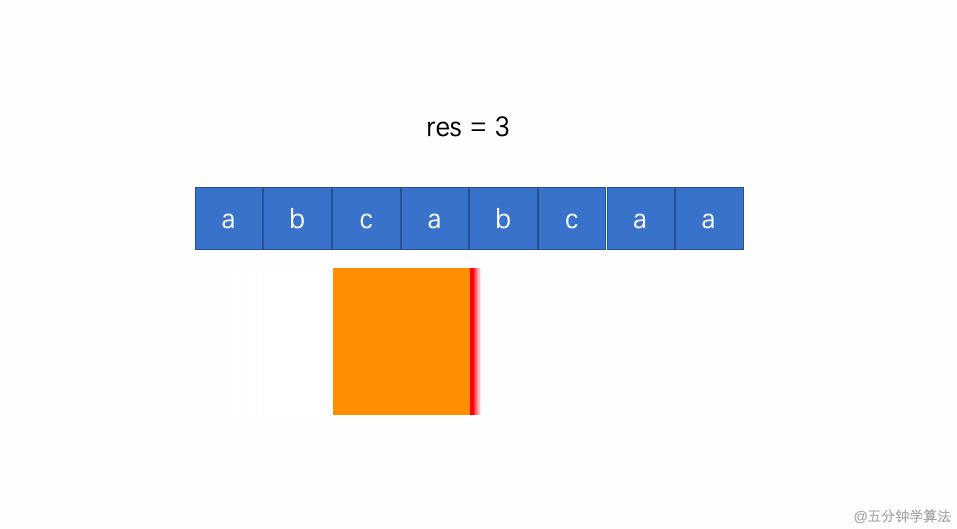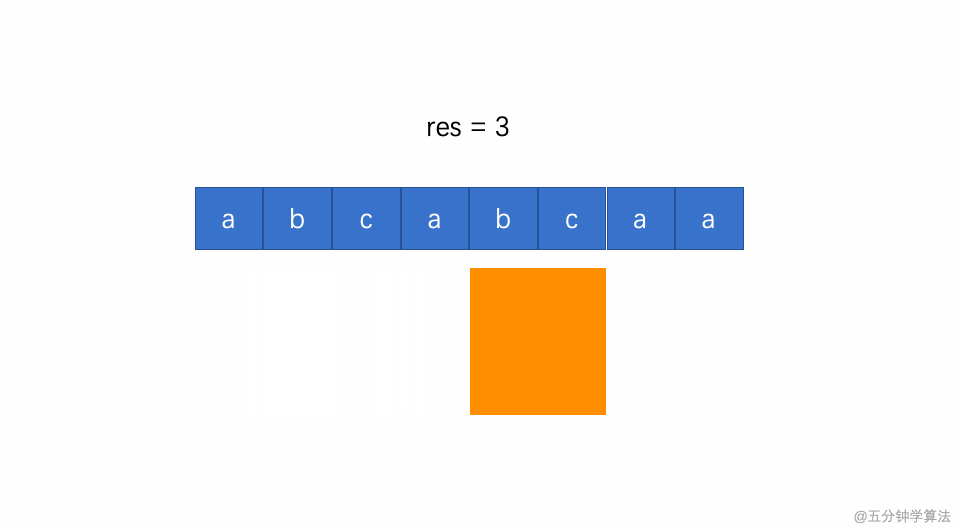
为了解决这个问题，我们需要增加一个整形数组来存放窗口中每个字符出现的下标，用于判断下一个字符是否在这个窗口中出现过。
代码如下：

#include 
using namespace std;
int c[26];        //c数组存窗口中每个字符出现的下标
int hdwindow(string s)
{
    memset(c,-1,sizeof(c)); 
    int ans=0,l=0,r=-1;     //l表示窗口的左端点，r表示窗口右端点
    for(int i=0;i<s.length();i++)
    {
        if(c[s[i]-'a']>=0&&c[s[i]-'a']>=l) //不为负值并且在窗口范围内表明出现过
            l=c[s[i]-'a']+1;     //窗口左边界改变
        r++;   //右边界加1
        c[s[i]-'a']=i;  //更新该字符出现的位置
        ans=max(ans,r-l);  //更新最大不重复子串长度
    }
    return ans;
}
int main()
{
    string s;
    cin >> s;
    int ans=hdwindow(s);
    printf("%d\n",ans);
    return 0;
}

代码模板

const int n=10e5;
int c[26];        //c数组存窗口中每个字符出现的下标
int a[N];
int hdwindow(string s)
{
    memset(c,-1,sizeof(c)); 
    int ans=0,l=0,r=-1;     //l表示窗口的左端点，r表示窗口右端点
    for(int i=0;i<s.length();i++)
    {
        if(c[s[i]-'a']>=0&&c[s[i]-'a']>=l) //不为负值并且在窗口范围内表明出现过
            l=c[s[i]-'a']+1;     //窗口左边界改变
        r++;   //右边界加1
        c[s[i]-'a']=i;  //更新该字符出现的位置
        ans=max(ans,r-l);  //更新最大不重复子串长度
    }
    return ans;
}

int hdwindow(int n,int k)
{
    int ans=0,sum=0;
    for(int i=1;i<=n;i++)
    {
        if(i-k>=1) 
            sum-=a[i-k];  //减去超出窗口的元素
        sum+=a[i];  //加上新添加的元素
        ans=max(ans,sum);  //更新答案
    }
    return ans;
}

单调队列

单调队列是单调的
害 就是维护一个单调递增或递减的序列，所有元素只入队一次，因此它的复杂度也是O(n)的。
正是因为它严格的单调性，所以一般用于解决RMQ(区间最值问题)，这么优秀的复杂度，其实也不是很难，思想类似于滑动窗口。

算法详解

这个单调队列，并不是数据结构里说的只允许先进先出的那种队列。
它可以从队头出去也可以从队尾出去，但只能在队尾加入元素。
emmmm 那什么元素需要出队呢？？？

假如维护一个单调递减的序列

• 对于队头来说，当然是超出这个区间的元素 从队头出队了。
• 对于队尾来说，对于加入新元素，如果队尾元素比该元素小，则从队尾出队，直到队尾元素大于新元素，将新元素加入到队列中。

举个栗子：
给你一个长度为 n 的序列 a，要你求每个连续的 k 个值中的最大值。
也就是连续区间的最值问题。

[1,3,−1,−3,5,3,6,7]       k=3

还是这组数据
维护一个单调队列 q[n] ,存放的是元素。p[n]存放队列中元素在原数组中的下标 。 l 模拟队列的队头指针 ，r 模拟队列的队尾指针。

• 如果队头元素超出k的范围 ， 队头指针向后移动
• 如果队尾元素比下一个元素小，那就出队，前一个元素更小所以必然不是该区间的最大值。直到队尾元素大于新元素，将新元素加入队列中。
• 如果当前的下标大于或等于k，输出队头元素，即为该区间的最大值。

对于这道题
1.当前队列为空，加入 [1]
2.队尾元素1小于3，所以在该区间中必然不会是最大值，1出队，加入[3]
3.队尾元素3大于-1，如果后面添加元素全部小于-1的话，-1可能为区间最大值，所以[-1]进队， 队列中元素[3,-1]，i >= k 输出队头元素 3 ；
4.队尾元素-1大于-3，理由同上，入队后，队列中元素[3,-1,-3]， i >= k ， 输出队头元素 3;
5.队头元素下标超出窗口范围出队，队尾元素-3小于5，-3出队，队尾元素-1小于5， -1出队，[5]入队， i >= k ， 输出队头元素 5 ;
6.队尾元素5大于3，3进队，队列中元素[5,3], i >= k ， 输出队头元素 5 ;
7.队尾元素3小于6，3出队， 队尾元素5小于6， 5出队，6入队 ，队列中元素[6] , i >= k ， 输出队头元素 6 ;
8.队尾元素6小于7，6出队， 7入队，队列中元素[7]， i >= k ， 输出队头元素 7 ;

void maxi()
{
    int l = 1, r = 0; 
    memset(q, 0, sizeof(q));
    memset(p, 0, sizeof(p));
    for (int i = 1; i <= n; ++i)
    {
        while(l<=r&&q[r]<=a[i])  //队尾元素小于新元素
            r--;  //队尾元素出队
        q[++r] = a[i];  //新元素入队
        p[r] = i;       //下标入队
        while(p[l]<=i-k)  //队头元素超出窗口范围
            l++; //队头元素出队
        if(i>=k)     //输出区间最值
            printf("%d ", q[l]);
    }
    printf("\n");
}

例题分析

洛谷p1886 单调队列模板题 ------------直达车.

题目描述
有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：
The array is [1,3,-1,-3,5,3,6,7], and k = 3。

输入格式
输入一共有两行，第一行有两个正整数 n, k。 第二行 n 个整数，表示序列 a

输出格式
输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

样例输入

8 3
1 3 -1 -3 5 3 6 7

样例输出

-1 -3 -3 -3 3 3
3 3 5 5 6 7

是不是感觉有点眼熟
第一个滑动窗口的例子和上边的讲解用的都是这个题的数据。 根据滑动窗口的思想和以上的描述，这题也很好写出来吧。
求每段连续区间的最值

再附上几道单调队列的题目：
p2032 扫描/求区间最大值/
P1440 求m区间内的最小值
p1714 切蛋糕/可变区间最大和/

模板代码

上题代码如下：

#include 
using namespace std;
int m,n,k;
int a[1000010],q[1000010],p[1000010];
void mini()
{
    int l = 1, r = 0;
    for (int i = 1; i <= n; ++i)
    {
        while(l<=r&&q[r]>=a[i])
            r--;
        q[++r] = a[i];
        p[r] = i;
        while(p[l]<=i-k)
            l++;
        if(i>=k)
            printf("%d ", q[l]);
    }
    printf("\n");
}

void maxi()
{
    int l = 1, r = 0;
    memset(q, 0, sizeof(q));
    memset(p, 0, sizeof(p));
    for (int i = 1; i <= n; ++i)
    {
        while(l<=r&&q[r]<=a[i])
            r--;
        q[++r] = a[i];
        p[r] = i;
        while(p[l]<=i-k)
            l++;
        if(i>=k)
            printf("%d ", q[l]);
    }
    printf("\n");
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    mini();
    maxi();
    return 0;
}