基于MATLAB和python输出曼德勃罗集
上帝的指纹——曼德勃罗集
曼德勃罗集可称是人类有史以来做出的最奇异、最瑰丽的几何图形,被人称为“上帝的指纹”、“魔鬼的聚合物”。 这个点集均出自公式:Zn+1=(Zn)^2+C
,对于非线性迭代公式Zn+1=(Zn)^2+C,所有使得无限迭代后的结果能保持有限数值的复数C的集合,构成曼德勃罗集。
上帝的指纹——曼德勃罗集
简介
这是一个迭代公式,式中的变量都是复数.这是一个大千世界,从他出发可以产生无穷无尽美丽图案,他是曼德勃罗特教授在二十世纪七十年代发现的.
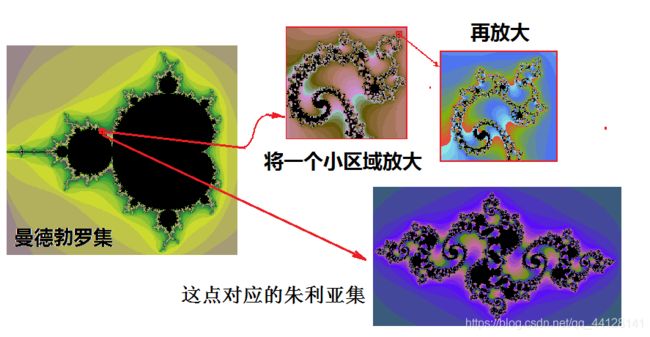

你看上图中,有的地方像日冕,有的地方像燃烧的火焰,只要你计算的点足够多,不管你把图案放大多少倍,都能显示出更加复杂的局部.这些局部既与整体不同,又有某种相似的地方,好像着梦幻般的图案具有无穷无尽的细节和自相似性.曼德勃罗特教授称此为"魔鬼的聚合物".为此,曼德勃罗特在1988年获得了"科学为艺术大奖".
图形是由美国数学家曼德勃罗特教授于1975年夏天一个寂静的夜晚,在冥思苦想之余翻看儿子的拉丁文字典是想到的,起拉丁文的原意是"产生无规则的碎片"。主要用运了分形理论和时间逃逸算法(能力有限,看不懂0.0)
MATLAB实现
代码
xc = 0; %图片中心点
yc = 0;
xoom = 1; %放大倍数
res = 3000; %分辨率
iter = 300; %序列项数
x0 = xc - 2 / xoom;
x1 = xc + 2 / xoom;
y0 = yc - 2 / xoom;
y1 = yc + 2 / xoom;
x = linspace(x0, x1, res);
y = linspace(y0, y1, res);
[xx, yy] = meshgrid(x, y);
C = xx + yy * 1i;
z = zeros(size(C));
N = uint8(zeros(res, res, 3));
color = uint8(round(rand(iter, 3) * 255));
for k = 1: iter
z = z.^2 + C;
[row, col] = find(abs(z) > 2);
k1 = zeros(size(row)) + 1;
k2 = zeros(size(row)) + 2;
k3 = zeros(size(row)) + 3;
p1 = sub2ind(size(N), row, col, k1);
N(p1) = color(k, 1);
p2 = sub2ind(size(N), row, col, k2);
N(p2) = color(k, 2);
p3 = sub2ind(size(N), row, col, k3);
N(p3) = color(k, 3);
z(abs(z) > 2) = 0;
C(abs(z) > 2) = 0;
end
imshow(N);
imwrite(N, 'test.png');
Python实现
代码
import numpy as np
import matplotlib.pyplot as plt
def iterator(c,r,max_iter):#定义逃逸时间函数,c为初始值,r为收敛半径,max_iter为最大迭代次数,返回逃逸时间
z=c #初始值
for iter in range(0,max_iter,1):
if abs(z)>r:break
z=z**2+c
return iter
def plot_mandelbrot(): #定义绘制mandelbrot图像
X=np.linspace(-1.75,1.05,5000) #实部范围,5000这个数要量力而行
Y=np.linspace(-1.25,1.25,5000) #虚部范围,5000这个数要量力而行
real,image=np.meshgrid(X, Y) #生成网格点坐标矩阵。
c=real+image*1j #构造复数
mandelbrot_set = np.frompyfunc(iterator, 3, 1)(c, 1.5, 100).astype(np.float) #frompyfunc(func, nin, nout),其中func是需要转换的函数,nin是函数的输入参数的个数,nout是此函数的返回值的个数,frompyfunc把Python里的函数(可以是自写的)转化成ufunc
plt.figure(dpi=500) #dpi设置分辨率尽可能高,细节显示更炫
plt.imshow(mandelbrot_set,extent=[-1.35, 1.35, -1.25, 1.25]) #extent用来调节显示框大小比例
#plt.axis('off') #是否显示坐标轴
plt.show()
if __name__=="__main__":
plot_mandelbrot()
总结
由于曼德勃罗集是由不断迭代所产生,所以如果生成无限放大的图片,需要增大分辨率,这是比较烧CPU的,建议电脑配置高的,尝试提高分辨率,不然电脑会卡死(本人深有体会 555,在Pycharm上提高分辨率,电脑会卡死;而在matlab中还没有发现卡死的情况),而且如果生成高分辨率的图像,所需要的的时间会让你崩溃。
生成高分辨率图像后,可以使用Ps或Pr、XaoS等其他软件进行处理放大,做出连续放大的视频。