WaWa的奇妙冒险(第五周集训自闭现场)
第五周周记(dp是真的难)
- (一)wlacm例题记录
- A-昆虫繁殖 (水题,递推)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B-邮票问题 (水题,有点像dp)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C-位数问题 (水题,递推)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- D-蜜蜂路线 (递推,高精度)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- E-极值问题 (递推)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- F-火车站 (递推)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- G-最短路径 (逆推,路径记录)
- Sample Input
- Sample Output
- 理解
- AC代码
- H-挖地雷 (逆推,路径记录)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- I-合唱队形 (双向lis)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- J-最大子阵和 (前缀和,最大连续子串和)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- K-搬寝室 (有依赖关系的背包?)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- L-暗黑破坏神 (分组背包,路径记录)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- M-科技庄园 (多重背包)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- N-天宝的预算 (依赖关系背包)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (二)vj例题记录
- A-Find The Multiple(同余定理) POJ - 1426
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B-Stacks of Flapjacks (分治) UVA - 120
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C-Building for UN (分治?) UVA - 1605
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- D-4 Values whose Sum is 0 (二分) UVA - 1152
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- E-Frog (基础dp和树状?) HDU - 2182
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- F-The King’s Ups and Downs (基础dp) HDU - 4489
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- G-Max Sum Plus Plus (多个最大连续子串和) HDU - 1024
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- H-Happy Matt Friends (树状dp?) HDU - 5119
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- I-Advanced Fruits (lcs,路径记录) HDU - 1503
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- J-Increasing Sequences(双向魔改lis)POJ - 1239
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- K-XHXJ's LIS(状压+数位+nlogn lis)HDU - 4352
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- L-最大报销额 (预处理01背包) HDU - 1864
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- M-Robberies (概率背包) HDU - 2955
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- N-Least common multiple (数论,分组背包,数据压缩) HDU - 3092
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- O-Shopping Offers (状态压缩,完全背包) POJ - 1170
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (三)其他地方的例题记录
- (四)一些收获
- 关于递推
- 关于dp
- 关于分治
- (五)感想
(一)wlacm例题记录
A-昆虫繁殖 (水题,递推)
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?0≤X≤20,1≤Y≤20,X≤Z≤50
Input
x,y,z的数值
Output
过Z个月以后,共有成虫对数
Sample Input
1 2 8
Sample Output
37
理解
简单的递推题吧,个人感觉是没啥难度(毕竟之前推过兔子繁殖),题意其实差距不大
不过有一个坑点,他这里的过x个月产卵y,指的是过x个月后,每个月产卵y个,刚开始没弄懂,纸上打了贼久的表
递推公式也比较简单 f[i] = f[i - 1] + f[i - x - 2]*y
AC代码
#include B-邮票问题 (水题,有点像dp)
设有已知面额的邮票m种,每种有n张,用总数不超过n张的邮票,能从面额1开始,最多连续组成多少面额。(1≤m≤100,1≤n≤100,1≤邮票面额≤255)
Input
第一行:m,n的值,中间用一空格隔开。
第二行:A[1…m](面额),每个数中间用一空格隔开。
Output
连续面额数的最大值
Sample Input
3 4
1 2 4
Sample Output
14
理解
emm 还是水题,不过看错题目,以为总和是255,卡了贼久(ce到自闭)
想法比较暴力,对每个面额做dp,发现某个面额所需要组成的钞票大于n就break,输出结果
(现在想想,直接多重背包改一改应该好了,然后从头往后找,当时不太会)
AC代码
#include C-位数问题 (水题,递推)
在所有的N位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
Input
读入一个数n(1≤n≤1000)
Output
输出有多少个数中有偶数个数字3。
Sample Input
2
Sample Output
73
理解
其实不算特别水,感觉有一点点像数位dp终极简化版
思路也很简单,从一位开始推,偶数个3有8个数,奇数个3有1个数
到两位数,就是一位数偶数个的情况下非3的数,再加上一位数为3情况下后面补一个3的数
两位数的奇数个3也同理
易得递推公式 even[i] = (even[i-1]*9 + odd[i-1])
odd[i] = (even[i] + odd[i-1]*9)
此处应该注意,因为最高位不能为0,所以推得过程应该是往后面添加数字
AC代码
#include D-蜜蜂路线 (递推,高精度)
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房M开始爬到蜂房N,M
Input
输入M,N的值,已知M 爬行有多少种路线。 1 14 377 已知m、n为整数,且满足下列两个条件: ① m、n∈{1,2,…,k},即1≤m,n≤k ②(n2-m*n-m2)2=1 你的任务是:编程输入正整数k(1≤k≤109),求一组满足上述两个条件的m、n,并且使m2+n2的值最大。例如,从键盘输入k=1995,则输出:m=987 n=1597。 输入正整数k(1≤k≤109) 输出满足条件的m、n,并且使m2+n2的值最大。 1995 m=987 火车从始发站(称为第1站)开出,在始发站上车的人数为a,然后到达第2站,在第2站有人上、下车,但上、下车的人数相同,因此在第2站开出时(即在到达第3站之前)车上的人数保持为a人。从第3站起(包括第3站)上、下车的人数有一定规律:上车的人数都是前两站上车人数之和,而下车人数等于上一站上车人数,一直到终点站的前一站(第n-1站),都满足此规律。现给出的条件是:共有N个车站,始发站上车的人数为a,最后一站下车的人数是m(全部下车)。试问x站开出时车上的人数是多少? 输入包含一行, 有四个正整数:a(a≤100),n(n≤20),m(m≤10000)和x(x≤19) 输出为一个整数,为x站开出时车上的人数。 1 6 7 4 4 下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。 10 minlong=19 在一个地图上有N个地窖(N<=1000),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。 输入有若干行。 第1行只有一个数字,表示地窖的个数N。 第2行有N个数,分别表示每个地窖中的地雷个数。 第3行至第N+1行表示地窖之间的连接情况。每行2个整数x,y(空格隔开),表示从地窖x可以到达地窖y。 输出有两行数据。 第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个减号"-"分隔,不得有多余的空格。 第二行只有一个数,表示能挖到的最多地雷数。 6 3-4-5-6 N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。 合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1, 2, …, K,他们的身高分别为T1, T2, …, TK,则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1≤i≤K)。 你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。 输入有多行,第一行是一个整数N(2 ≤ N ≤ 100),表示同学的总数。第二行有n个整数,用空格分隔,第i个整数Ti(130 ≤ Ti ≤ 230)是第i位同学的身高(厘米)。 输出只有一行,这一行只包含一个整数,就是最少需要几位同学出列。 8 4 有一个包含正数和负数的二维数组。一个子矩阵是指在该二维数组里,任意相邻的下标是1*1或更大的子数组。一个子矩阵的和是指该子矩阵中所有元素的和。本题中,把具有最大和的子矩阵称为最大子矩阵。 输入包含多组测试数据。每组输入的第一行是一个正整数N(1<=N<=100),表示二维方阵的大小。接下来N行每行输入N个整数,表示数组元素,范围为[-127,127]。 输出最大子阵和。 4 15 搬寝室是很累的,xhd深有体会.时间追述2006年7月9号,那天xhd迫于无奈要从27号楼搬到3号楼,因为10号要封楼了.看着寝室里的n件物品,xhd开始发呆,因为n是一个小于2000的整数,实在是太多了,于是xhd决定随便搬2k件过去就行了.但还是会很累,因为2k也不小是一个不大于n的整数.幸运的是xhd根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如xhd左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的xhd希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度),请告诉他吧。 每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数). 对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行. 5 1 492804 无聊中的小x玩起了Diablo III… 第1行 用空格隔开的两个整数n和m个金币 c[i] p[i] w[i][1] w[i][2] … w[i][p[i]] 第1行输出一个整数,即最大效果值。 第2-n+1行输出购买魔法书的最优选择。 3 10 11 Life是codevs的用户,他是一个道德极高的用户,他积极贯彻党的十八大精神,积极走可持续发展道路,在他的不屑努力下STN终于决定让他在一片闲杂地里种桃,以亲身实践种田的乐趣,厉行节约,告诉人们节约的重要性! 春华秋实,在这个金秋的季节,Life带者他的宠物——PFT到了他的试验田,当他看见自己的辛勤成果时,心里是那个高兴啊! 这时Life对他的宠物PFT说:“你想不想吃桃啊?” PFT兴奋的说:“好啊!” Life说:“好吧,但是我只给你一定的时间,你必须在规定的时间之内回到我面前,否则你摘的桃都要归我吃!” PFT思考了一会,最终答应了! 由于PFT的数学不好!它并不知道怎样才能在规定的时间获得最大的价值,但你是一个好心人,如果你帮助它,你的RP一定会暴涨的! 对于这个可以RP暴涨机会,你一定不会错过的是不是? 由于PFT不是机器人,所以他的体力并不是无限的,他不想摘很多的桃以至体力为0,而白白把桃给Life。同时PFT每次只能摘一棵桃树,每棵桃树都可以摘K次(对于同一棵桃每次摘的桃数相同)。每次摘完后都要返回出发点(PFT一次拿不了很多)即Life的所在地(0,0){试验田左上角的桃坐标是(1,1)}。 PFT每秒只能移动一个单位,每移动一个单位耗费体力1(摘取不花费时间和体力,但只限上下左右移动)。 第1行:四个数为N,M,TI,A 分别表示试验田的长和宽,Life给PFT的时间,和PFT的体力。 一个数:PFT可以获得的最大的桃个数。 4 4 13 20 10 天宝很高兴,新房马上可以拿钥匙了,天宝可以有自己的小房间了。另外妈妈跟她说:“你自己的房间布置,你说了算。要买的物品只要不超过n元就行”。一大早,天宝就开始预算了,她把想买的物品分为两类:大件与配件,配件是从属于某个大件的,下表就是一些大件与配件的例子。如果要买归类为配件的物品,必须先买该配件所属的大件。 输入的第1行为两个正整数n和m(分别表示总钱数和希望购买商品的数量) 接下来是m行,第i行给出了编号为i-1的商品的信息。 每行3个非负整数 v、p和 q (其中v表示该商品的价格,p表示该商品的重要性,q表示该商品是主件还是附件。如果q=0,表示该商品为主件,如果q> 0,表示该商品为附件,q是所属主件的编号) 输出只有一个正整数,即不超过预算N元的每件商品的重要性与价格的乘积总和的最大值。 1500 7 6200 Given a positive integer n, write a program to find out a nonzero multiple m of n whose decimal representation contains only the digits 0 and 1. You may assume that n is not greater than 200 and there is a corresponding m containing no more than 100 decimal digits. The input file may contain multiple test cases. Each line contains a value of n (1 <= n <= 200). A line containing a zero terminates the input. For each value of n in the input print a line containing the corresponding value of m. The decimal representation of m must not contain more than 100 digits. If there are multiple solutions for a given value of n, any one of them is acceptable. 2 10 Stacks and Queues are often considered the bread and butter of data structures and find use in architecture,parsing, operating systems, and discrete event simulation. Stacks are also important in the theory of formal languages. The input consists of a sequence of stacks of pancakes. Each stack will consist of between 1 and 30 pancakes and each pancake will have an integer diameter between 1 and 100. The input is terminated by end-of-file. Each stack is given as a single line of input with the top pancake on a stack appearing first on a line, the bottom pancake appearing last, and all pancakes separated by a space. For each stack of pancakes, the output should echo the original stack on one line, followed by some sequence of flips that results in the stack of pancakes being sorted so that the largest diameter pancake is on the bottom and the smallest on top. For each stack the sequence of flips should be terminated by a ‘0’ (indicating no more flips necessary). Once a stack is sorted, no more flips should be made. 1 2 3 4 5 1 2 3 4 5 The United Nations has decided to build a new headquarters in Saint Petersburg, Russia. It will have a form of a rectangular parallelepiped and will consist of several rectangular floors, one on top of another. Input consists of several datasets. Each of them has a single integer number n (1 ≤ n ≤ 50) — the number of countries that are hosted in the building. On the first line of the output for each dataset write three integer numbers h, w, and l — height, width and length of the building respectively. 4 2 2 2 中途想遇法的写法 https://blog.csdn.net/wjmwsgj/article/details/78280420 The SUM problem can be formulated as follows: given four lists A, B, C, D of integer values, compute how many quadruplet (a, b, c, d) ∈ A × B × C × D are such that a + b + c + d = 0. In the following, we assume that all lists have the same size n. The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs. For each test case, your program has to write the number quadruplets whose sum is zero. 1 5 A little frog named Fog is on his way home. The path’s length is N (1 <= N <= 100), and there are many insects along the way. Suppose the original coordinate of Fog is 0. Fog can stay still or jump forward T units, A <= T <= B. Fog will eat up all the insects wherever he stays, but he will get tired after K jumps and can not jump any more. The number of insects (always less than 10000) in each position of the path is given. The input consists of several test cases. each test case: 1 8 第二个写法 The king has guards of all different heights. Rather than line them up in increasing or decreasing height order, he wants to line them up so each guard is either shorter than the guards next to him or taller than the guards next to him (so the heights go up and down along the line). For example, seven guards of heights 160, 162, 164, 166, 168, 170 and 172 cm. could be arranged as: For example, if there are four guards: 1, 2, 3,4 can be arrange as: 1324, 2143, 3142, 2314, 3412, 4231, 4132, 2413, 3241, 1423 For this problem, you will write a program that takes as input a positive integer n, the number of guards and returns the number of up and down orders for n guards of differing heights. The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set consists of single line of input containing two integers. The first integer, D is the data set number. The second integer, n (1 <= n <= 20), is the number of guards of differing heights. For each data set there is one line of output. It contains the data set number (D) followed by a single space, followed by the number of up and down orders for the n guards. 4 1 1 Now I think you have got an AC in Ignatius.L’s “Max Sum” problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem. Given a consecutive number sequence S 1, S 2, S 3, S 4 … S x, … S n (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ S x ≤ 32767). We define a function sum(i, j) = S i + … + S j (1 ≤ i ≤ j ≤ n). Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i 1, j 1) + sum(i 2, j 2) + sum(i 3, j 3) + … + sum(i m, j m) maximal (i x ≤ i y ≤ j x or i x ≤ j y ≤ j x is not allowed). But I`m lazy, I don’t want to write a special-judge module, so you don’t have to output m pairs of i and j, just output the maximal summation of sum(i x, j x)(1 ≤ x ≤ m) instead. _ Each test case will begin with two integers m and n, followed by n integers S 1, S 2, S 3 … S n. Output the maximal summation described above in one line. 1 3 1 2 3 6 附上大佬blog https://blog.csdn.net/codeswarrior/article/details/80310401 Matt has N friends. They are playing a game together. Each of Matt’s friends has a magic number. In the game, Matt selects some (could be zero) of his friends. If the xor (exclusive-or) sum of the selected friends’magic numbers is no less than M , Matt wins. Matt wants to know the number of ways to win. The first line contains only one integer T , which indicates the number of test cases. For each test case, the first line contains two integers N, M (1 ≤ N ≤ 40, 0 ≤ M ≤ 10 6). In the second line, there are N integers ki (0 ≤ k i ≤ 10 6), indicating the i-th friend’s magic number. For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y indicates the number of ways where Matt can win. 2 Case #1: 4 The company “21st Century Fruits” has specialized in creating new sorts of fruits by transferring genes from one fruit into the genome of another one. Most times this method doesn’t work, but sometimes, in very rare cases, a new fruit emerges that tastes like a mixture between both of them. A combination of a cranberry and a boysenberry would therefore be called a “boysecranberry” or a “craboysenberry”, for example. Your job is to write a program that computes such a shortest name for a combination of two given fruits. Your algorithm should be efficient, otherwise it is unlikely that it will execute in the alloted time for long fruit names. Each line of the input contains two strings that represent the names of the fruits that should be combined. All names have a maximum length of 100 and only consist of alphabetic characters. Input is terminated by end of file. For each test case, output the shortest name of the resulting fruit on one line. If more than one shortest name is possible, any one is acceptable. apple peach appleach Given a string of digits, insert commas to create a sequence of strictly increasing numbers so as to minimize the magnitude of the last number. For this problem, leading zeros are allowed in front of a number. Input will consist of multiple test cases. Each case will consist of one line, containing a string of digits of maximum length 80. A line consisting of a single 0 terminates input. For each instance, output the comma separated strictly increasing sequence, with no spaces between commas or numbers. If there are several such sequences, pick the one which has the largest first value;if there’s a tie, the largest second number, etc. 3456 3,4,5,6 #define xhxj (Xin Hang senior sister(学姐)) First a integer T(T<=10000),then T lines follow, every line has three positive integer L,R,K.( For each query, print “Case #t: ans” in a line, in which t is the number of the test case starting from 1 and ans is the answer. 1 Case #1: 139 现有一笔经费可以报销一定额度的发票。允许报销的发票类型包括买图书(A类)、文具(B类)、差旅(C类),要求每张发票的总额不得超过1000元,每张发票上,单项物品的价值不得超过600元。现请你编写程序,在给出的一堆发票中找出可以报销的、不超过给定额度的最大报销额。 测试输入包含若干测试用例。每个测试用例的第1行包含两个正数 Q 和 N,其中 Q 是给定的报销额度,N(<=30)是发票张数。随后是 N 行输入,每行的格式为: 对每个测试用例输出1行,即可以报销的最大数额,精确到小数点后2位。 200.00 3 123.50 The aspiring Roy the Robber has seen a lot of American movies, and knows that the bad guys usually gets caught in the end, often because they become too greedy. He has decided to work in the lucrative business of bank robbery only for a short while, before retiring to a comfortable job at a university. His mother, Ola, has decided upon a tolerable probability of getting caught. She feels that he is safe enough if the banks he robs together give a probability less than this. The first line of input gives T, the number of cases. For each scenario, the first line of input gives a floating point number P, the probability Roy needs to be below, and an integer N, the number of banks he has plans for. Then follow N lines, where line j gives an integer Mj and a floating point number Pj . For each test case, output a line with the maximum number of millions he can expect to get while the probability of getting caught is less than the limit set. Notes and Constraints 3 2 Partychen like to do mathematical problems. One day, when he was doing on a least common multiple(LCM) problem, he suddenly thought of a very interesting question: if given a number of S, and we divided S into some numbers , then what is the largest LCM of these numbers? partychen thought this problems for a long time but with no result, so he turned to you for help! There are many groups of test case.On each test case only two integers S( 0 < S <= 3000) and M( 2<=M<=10000) as mentioned above. Output the largest LCM modulo M of given S. 6 23 6 Hint: you can divied 6 as 1+2+3 and the LCM(1,2,3)=6 is the largest so we output 6%23=6. Your program is to read from standard input. The first line contains the number b of different kinds of products in the basket (0 <= b <= 5). Each of the next b lines contains three values c, k, and p. The value c is the (unique) product code (1 <= c <= 999). The value k indicates how many items of this product are in the basket (1 <= k <= 5). The value p is the regular price per item (1 <= p <= 999). Notice that all together at most 5*5=25 items can be in the basket. The b+2nd line contains the number s of special offers (0 <= s <= 99). Each of the next s lines describes one offer by giving its structure and its reduced price. The first number n on such a line is the number of different kinds of products that are part of the offer (1 <= n <= 5). The next n pairs of numbers (c,k) indicate that k items (1 <= k <= 5) with product code c (1 <= c <= 999) are involved in the offer. The last number p on the line stands for the reduced price (1 <= p <= 9999). The reduced price of an offer is less than the sum of the regular prices. Your program is to write to standard output. Output one line with the lowest possible price to be paid. 2 14 最早接触的递推题就是斐波那契数列了,当时找到规律后是模拟了求数的过程,并未对其有所思考,当后面遇到兔子繁殖问题的时候,做的一脸懵逼,完全不会写,看完题解知道就是斐波那契数列的时候,确实被震惊了一下,在后面的学习中,逐渐认识到递推的魅力所在,但掌握起来也很难。即便是这种滚了一遍入了个门,也感觉是找起来不容易,但或多或少有点感受吧。 1.对于任何递推问题,本质上而言是可以通过推小规模的情况得出递推公式的,因为这实际上是一个通式,可能对于不同的问题难度区别较大,但找递推公式的时候,模拟小规模的情况不失为一种好方法。 2.多条件情况下分治,并非所有的递推都是单一条件,在多条件情况下,我们找起来难度会大的多,这时候分开考虑可能会有奇效,最好的例子个人感觉是学堂在线程序设计课递推板块的青蛙过河问题。 3.当你确实无法从一些数学公式(或者其他的东西,不过目前遇到的一般都是数学公式)中找出一种递推的规律时,打表不失为一种好办法(极值问题和上周的百度之星都打表找到的规律)。 按照现在学习的感受而言,递推,其实和贪心之类的类似,一种看悟性和经验的东西,不过递推可能会稍有迹可循一点,小规模的推理确实对于找递推公式有极大地帮助,现在的水平也还是入门级的萌新,之后多做点题,多思考来强化递推的能力吧 这周也是dp入门的一周,准备来说,这周也就学会了一点普通dp和背包dp的模板,也算有一点点心得体会 1.dp公式(状态转移公式),本质上而言,个人感觉dp就像二维的贪心?贪心就是一种线性的前进方式,而dp不同,他是对每个起始状态的中间量都开一条线出来(类似背包dp里面将背包的体积分为0~n),对每次的选择多条线选出最优,以实现最后全局的最优,而状态转移恰如其名,每次都选择各条线的最优状态进行继承。 2.条件转移的考虑方式,在状态转移方面,一定要注意,当前状态能从什么状态得到,以及之前的状态之后会有几个变化,背包问题很简单(取或不取、取几个),而其他dp则要相对问题而言确认状态应该往几个方法转变,以及该状态之前的状态该从哪里取 3.dp公式的构架,准确来说,dp公式很像递推公式,但又有不同,递推公式很多情况下是线性的通式,只要你推出来了,无脑往里面代就好了。而dp公式呢,则要根据状态转移的方向(单方向、多方向)进行考虑,所以可能写的判断会多很多。但本质上而言,小规模的公式推理同样适用于dp,且一般情况下非常好用(入门级)。 4.dp的魔改,一般都是在原dp的框架上,加上后改变要转移的状态,遇上也不用慌,先把原dp的框架构架起来,再慢慢修改细节,很多时候写起来会很难,可以考虑分块解决,按问题的优先级一个个来,最后可能会tle或者wa,但离ac会近很多很多 关于基础dp 差不多能讲的都讲了,剩下看悟性了,比起其他dp类型的套模板,很多基础dp没有固定模板,构架起来会难很多,老老实实从小规模往后推即可。(也有时候是其他dp模板的魔改,你看不出来,记得写前先把你熟悉的dp模板考虑一遍) 关于背包dp 实际上,基础的背包问题很死板,单纯的裸题稍稍魔改很容易做,背包套背包的行为稍加考虑,分开处理也是能解决的,真正难的是后面类似数位、状压等dp和背包问题结合之后的题目,可能是现在练得还不够,再加上后面的dp类型还没学,写起来很有压力 关于数位、状压、区间、双塔等dp 还没学,玩不来,等死ing,数位只能敲敲模板,状压只能暴力hash,蒟蒻说的就是我 好吧emm 我以为这周会有更多分治的内容,但貌似就新开了一个题集给我们写了一下就没了,emm 但我做分治题的时候思路还是很差,很多时候想都都是暴力解法。。。 这方面真的不太擅长,现在的集训也是大方向如个门,后面慢慢学习吧。。。 大概就以下几点 2.关于dp,怎么说呢,感觉线性dp算是入了个门吧,从以前只会写一些裸背包题,到现在可以写一些简单的基础dp,背包套背包,双dp结合的dp,应该也算一种小小的进步吧。就是后面dp太难了(区间、数位之类的),之后再慢慢来吧,感觉入门题是可以写了,后面就是花时间深入学习了 3.关于分治,emm 这个真的好菜,脑子里暴力解法居多,二分啥的好难啊。。。 之后再慢慢练了,感觉还是脑子转不过弯来,容易在这上面卡死(比起贪心感觉操作起来难好多) 4.关于数据结构,emm 我得说CCPC打自闭了,花了一小时研究的kmp成功tle,之后才知道是sa+st+主席树(三个听都没听过的东西,我写个锤子啊),听说还有一题是线段树(这个也没听过),死在数据结构上是真的绝望,这东西不是靠你的思维能够简单解决的,系统的学习后面进阶的数据结构才能完成ac这些魔鬼题目。 (革命尚未成功,同志尚需努力[狗头])Output
Sample Input
Sample Output
理解
递推公式很好找,f[n] = f[n-1] + f[n-2] 明显的斐波那契数列
关键是他的M和N的差值可能非常大,所以要手写高精度加法来存
AC代码
#include E-极值问题 (递推)
Input
Output
Sample Input
Sample Output
n=1597理解
emm 这道题过的很侥幸,枚举了小规模的m,n
发现貌似就是一个小于m + n小于k的斐波那契数列,f[n-1] = f[m]
后来看了大佬的题解,才明白,那个数学公式可以递推

附上大佬题解和blog https://www.cnblogs.com/huashanqingzhu/p/4739977.htmlAC代码
#include F-火车站 (递推)
Input
Output
Sample Input
Sample Output
理解
思路比较简单,就是一个一元一次函数求解来着,只要算出第二站上车的人数是多少就好了
设第二站上车人数为k,第一站为a,手写一个小规模的表就能看出规律了,上车人数减去下车人数的差其a和k的系数是一个斐波那契数列
算处最后一站之前那站时的人数,就可以算出k了,代入递推公式求解即可
AC代码
#include G-最短路径 (逆推,路径记录)


Sample Input
0 2 5 1 0 0 0 0 0 0
0 0 0 0 12 14 0 0 0 0
0 0 0 0 6 10 4 0 0 0
0 0 0 0 13 12 11 0 0 0
0 0 0 0 0 0 0 3 9 0
0 0 0 0 0 0 0 6 5 0
0 0 0 0 0 0 0 0 10 0
0 0 0 0 0 0 0 0 0 5
0 0 0 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0 0 0Sample Output
1 3 5 8 10理解
有点意思的逆推题,最早看见的逆推题是洛谷上的排地雷,这个稍微简单一点,从后往前找最优状态就好了
路径记录的话,因为path里面存的时候后面的位置,所以循环输出即可
AC代码
#include H-挖地雷 (逆推,路径记录)
Input
Output
Sample Input
5 10 20 5 4 5
1 2
1 4
2 4
3 4
4 5
4 6
5 6
0 0Sample Output
34理解
这题和上路其实差不多,也就是我在洛谷上看见过的逆推题(在acm遇上了。。。),这题和上题唯一的区别
是对于到不了的点,应该赋自身的雷数,因为他没有固定开始的起点和终点
AC代码
#include I-合唱队形 (双向lis)
Input
Output
Sample Input
186 186 150 200 160 130 197 220Sample Output
理解
emm 思路比较简单,确保能留的人最多,就可以确定去掉的人最少了,题目就转换成了双向lis
刚开始wa了几发,因为想错了,以为是一个lis和一个lds,后面仔细思考了一下,正向的lds其实是记录左
边比该数大的数,而我们要求的右边比该数小的数,改成反向lis成功ac
AC代码
#include J-最大子阵和 (前缀和,最大连续子串和)
例如:
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
这个数组的最大子矩阵为:
9 2
-4 1
-1 8
其和为15。Input
Output
Sample Input
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2Sample Output
理解
因为之前做牛客的最大子阵和的时候已经看过题解。。。
写这题的时候难度emm 真的不大
大概思路,先对每一列求前缀和,然后选择行数进行列前缀和差的求最大连续子串和,难度不大
AC代码
#include K-搬寝室 (有依赖关系的背包?)
Input
Output
Sample Input
18467 6334 26500 19169 15724
7 1
29358 26962 24464 5705 28145 23281 16827
0 0Sample Output
1399489理解
这题刚开始写的没想到背包那去,因为要隔两层进行状态转移,后面越看越想依赖背包的魔改
想要使(a-b)^2最小,差值最小即可,一个很简单的思路,排序即可
重点是选完某件物品之后,他前面那个也就被选掉了,要杜绝这种重复选的可能性
emm 做法比较简单,用当前是第几个物品,来限制当前能取第几对
AC代码
#include L-暗黑破坏神 (分组背包,路径记录)
游戏的主人公有n个魔法
每个魔法分为若干个等级,第i个魔法有p[i]个等级(不包括0)
每个魔法的每个等级都有一个效果值,一个j级的i种魔法的效果值为w[i][j]
魔法升一级需要一本相应的魔法书
购买魔法书需要金币,第i个魔法的魔法书价格为c[i]
而小x只有m个金币(好孩子不用修改器)
你的任务就是帮助小x决定如何购买魔法书才能使所有魔法的效果值之和最大
开始时所有魔法为0级 效果值为0Input
以下n行 描述n个魔法
第i+1行描述 第i个魔法 格式如下Output
Sample Input
1 3 1 2 2
2 3 2 4 6
3 3 2 1 10Sample Output
1
0
3理解
比较简单的分组背包问题,就路径记录难一点,和之前的 “机器分配” 其实做法完全一致,因为喜欢大菠萝
就记了这题。
分组背包的思路也很简单,对于每个组合内的所有物品做一次01背包dp即可
分组背包写一维即可,在开一个二维的数组方便递归输出路径就好
AC代码
#include M-科技庄园 (多重背包)
Input
下面一个N行M列的矩阵桃田。表示每次每棵桃树上能摘的桃数。
接下来N行M列的矩阵,表示每棵桃最多可以采摘的次数K。Output
Sample Input
10 0 0 0
0 0 10 0
0 0 10 0
0 0 0 0
1 0 0 0
0 0 2 0
0 0 4 0
0 0 0 0Sample Output
理解
emm 前面也是有一些多重背包题,但大多是裸题,索性记一下这题
这题表面上来看,是一个二维费用的多重背包,但消耗时间和体力是相同的,emm 所以取两者最小值记为时
间即可,又因为要规定时间内回到出发点,且往返时间至少为2,所以可以认为给PFT留一点体力即可(背包
上限减一)
(不过不会单调队列优化,只能用二进制优化。。。之后一定好好学)
AC代码
#include N-天宝的预算 (依赖关系背包)
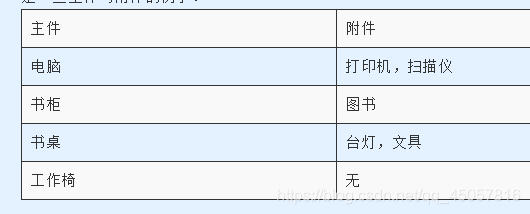
大件可以有2个配件、1个配件或0个配件。天宝好高兴但是又很苦恼,只有n元怎么选呢。好朋友给她提了个建议,让她把物品设定一个重要性,分为5等:用1~5表示,数字越大越重要。天宝又在网上查到了各件物品的价格(都是10元的整数倍)。天宝希望在不超过n元前提下,使每件物品的价格与重要性乘积的总和最大。请你帮助天宝设计一个满足要求的购物单。Input
Output
Sample Input
500 1 0
400 4 0
300 5 1
400 5 1
200 5 0
500 4 0
400 4 0Sample Output
理解
第二次写依赖关系背包吧(大概),这题emm 其实可以想的很简单,因为一个主件最多也就两个附件,算上
所有可能性也行4中可能,可以转成01背包里的物品简单dp
但是,这样的做法显然不够优秀,因为一旦附件数量不加限制,但时间复杂度贼大
因为之前看过背包9讲,换个思路,对于主件和附件的结合体,我们当做一个子问题来进行一次01背包即可
操作方面可以调用一个临时的背包数组,在减去主件价格的情况下,对背包内的物品做01背包dp,然后返回
原背包的时候,记得把主件质量加上做一次dp即可(忘记加上主件wa三次。。。是我太菜了)
AC代码
#include (二)vj例题记录
A-Find The Multiple(同余定理) POJ - 1426
Input
Output
Sample Input
6
19
0Sample Output
100100100100100100
111111111111111111理解
上次学dfs和bfs的时候,拿着学长讲的dfs代码水了过去,这次emm 用了同余定理
(a*b)%n = (a%n *b%n)%n;
(a+b)%n = (a%n +b%n)%n;
其实就是余数的运算法则,然后自己构架一个不断增加的十进制下的01串取余即可,也不用担心溢出问题
就是构架01串需要想想,比起dfs简单粗暴的构架方式而言,用数组构架稍稍难一点
AC代码
#include B-Stacks of Flapjacks (分治) UVA - 120
This problem involves both butter and sustenance in the form of pancakes rather than bread in addition to a finicky server who flips pancakes according to a unique, but complete set of rules.
Given a stack of pancakes, you are to write a program that indicates how the stack can be sorted so that the largest pancake is on the bottom and the smallest pancake is on the top. The size of a pancake is given by the pancake’s diameter. All pancakes in a stack have different diameters.
Sorting a stack is done by a sequence of pancake “flips”. A flip consists of inserting a spatula between two pancakes in a stack and flipping (reversing) all the pancakes on the spatula (reversing the sub-stack). A flip is specified by giving the position of the pancake on the bottom of the sub-stack to be flipped (relative to the whole stack). The pancake on the bottom of the whole stack has position 1 and the pancake on the top of a stack of n pancakes has position n.
A stack is specified by giving the diameter of each pancake in the stack in the order in which the pancakes appear.
For example, consider the three stacks of pancakes below (in which pancake 8 is the top-most pancake of the left stack):

The stack on the left can be transformed to the stack in the middle via flip(3). The middle stack can be transformed into the right stack via the command flip(1).Input
Output
Sample Input
5 4 3 2 1
5 1 2 3 4Sample Output
0
5 4 3 2 1
1 0
5 1 2 3 4
1 2 0理解
刚开始真的没懂这题分治该怎么写,尝试自己推了几次小规模的数据,也没懂(先把小的塞前面和先把大的塞后面),后来看了题解,处理完最大数之后
,再处理次大数,形成一个处理完n再解决n-1规模的问题,从最大数开始放置就能得到结果
说实话,当时没懂,没想通为啥这样能步数最少,后面用了atcoder逆推的思路emm 感觉勉强懂一点
关键是分情况处理
(1)n大的数正好在数组顶端,直接进行反转到n位置即可
(2)n大的数不在数组顶端,先移到数组顶端,在移到n位置
不会对后面已经排好的序列产生影响(感觉贼像选择排序)
AC代码
#include C-Building for UN (分治?) UVA - 1605
Each floor is a rectangular grid of the same dimensions, each cell of this grid is an office.
Two offices are considered adjacent if they are located on the same floor and share a common wall,or if one’s floor is the other’s ceiling.
The St. Petersburg building will host n national missions. Each country gets several offices that form a connected set.
Moreover, modern political situation shows that countries might want to form secret coalitions. For that to be possible, each pair of countries must have at least one pair of adjacent offices, so that they can raise the wall or the ceiling they share to perform secret pair-wise negotiations just in case they need to.
You are hired to design an appropriate building for the UN.Input
Output
h descriptions of floors should follow. Each floor description consists of l lines with w characters on each line. Separate descriptions of adjacent floors with an empty line.
Use capital and small Latin letters to denote offices of different countries. There should be at most 1 000 000 offices in the building. Each office should be occupied by a country. There should be exactly n different countries in the building. In this problem the required building design always exists.
Print a blank line between test cases.Sample Input
Sample Output
AB
CC
zz
zz理解
这题一开始看的一脸懵逼,保证每两个国家都有办公室相邻,且国家房间相连?
样例看的一脸懵逼,后来看题目有特判定,姑且写了一个每层分配一个国家为行,再每个国家分配一行的想法,想试试左上右下这种算不算相连
虽然成功ac,但还是一脸懵逼
(后来看了题解说是 中途相遇法 完全不懂)
AC代码
#include D-4 Values whose Sum is 0 (二分) UVA - 1152
Input
The first line of the input file contains the size of the lists n (this value can be as large as 4000).
We then have n lines containing four integer values (with absolute value as large as 228) that belong respectively to A, B, C and D.Output
The outputs of two consecutive cases will be separated by a blank line.Sample Input
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45Sample Output
Sample Explanation: Indeed, the sum of the five following quadruplets is zero: (-45, -27, 42, 30),
(26, 30, -10, -46), (-32, 22, 56, -46), (-32, 30, -75, 77), (-32, -54, 56, 30).理解
刚开始看的一脸懵逼想着四重循环肯定超时,可以写成n^3,但感觉也可能超
然后大佬告诉我对列二分即可,c和d先求和,排序准备,然后枚举a和b的和,用upper和lower找符合要求的值的个数
这还跑了进2.5s,emm 感觉n^3高概率tle
AC代码
#includeE-Frog (基础dp和树状?) HDU - 2182
How many insects can Fog eat at most?
Note that Fog can only jump within the range [0, N), and whenever he jumps, his coordinate increases.Input
The first line contains an integer T indicating the number of test cases.
For each test case:
The first line contains four integers N, A, B(1 <= A <= B <= N), K (K >= 1).
The next line contains N integers, describing the number of insects in each position of the path.Output
Output one line containing an integer - the maximal number of insects that Fog can eat.Sample Input
4 1 2 2
1 2 3 4Sample Output
理解
刚开始的思路是写一个二维的dp,dp[i][j],i为距离,j为步数
因为一些无效跳跃的值,不会影响结果,所以即便出现dp[1][4]这种,也不会对后面的值产生干扰,所以成功dp
后来做了最后两题之后,感觉可以换个写法,写成类似数状dp?(还没学,感觉像树的结构)
前者的dp公式 dp[j][l] = max(dp[j][l],dp[i][l-1]+val[j]) i+a <= j <= i+b;
后者其实差不多,但写成了一维,这里非法跳跃的值不会被计入,变成了空挑
dp公式为 dp1[l] = max(dp1[l],dp[j] + val[l]); dp为步数减1那一层
不过后者运行时间明显长一点
AC代码
#include #include F-The King’s Ups and Downs (基础dp) HDU - 4489

or perhaps:

The king wants to know how many guards he needs so he can have a different up and down order at each changing of the guard for rest of his reign. To be able to do this, he needs to know for a given number of guards, n, how many different up and down orders there are:Input
Output
Sample Input
1 1
2 3
3 4
4 20Sample Output
2 4
3 10
4 740742376475050理解
这道题emm 想了很久,后面发现没那么难,就和组合排列的知识结合一下就好
首先明确一点,n可能的排列方式总数能被(高低高)和(低高低)对半分,可以拿小规模验证一下
之后考虑缩小规模,例如在123之后插入1个4
4可以插入在1前,2前,3前,3后,简而言之,对于插入的第n个人,有n个位置可以放
且当我们把4放入时,前后的排序规则必然定死,(高低高和低高低两者之一),之后考虑n-1个人中取x个人排在前面的所有可能性即可,也就是排列组
合了
又因为1个人为1,除2会出现数据丢失的情况,为了保险起见,dp公式记录总数的一般也就是n个人时(高低高)或者(低高低)的值即可
dp转移公式
for(int j = 1;j <= i;j++)
sum += dp[j - 1]*dp[i - j]*C[i - 1][j - 1];
AC代码
#include G-Max Sum Plus Plus (多个最大连续子串和) HDU - 1024
Input
Process to the end of file.Output
Sample Input
2 6 -1 4 -2 3 -2 3Sample Output
8理解
题目看的一脸懵逼,能想到是求多个最大连续子串和,但完全不知道怎么操作
后面看完大佬的题解,实际上就是最大连续子串和的写法,外面再套一个最大连续子串和,形成dp
偷来的状态转移公式 dp[i][j]=max(dp[i][j-1]+a[j],max(dp[i-1][k])+a[j]) (0AC代码
#include H-Happy Matt Friends (树状dp?) HDU - 5119
Input
Output
Sample Input
3 2
1 2 3
3 3
1 2 3### Sample Output
2.00 2.00 1.41Sample Output
Case #2: 2理解
写完前面的robort之后,写这题感觉emm 简单了很多,同样是模仿一个树状的结构,一层一层进行,因为亦
或,你不知道会不会干扰的其他求值,所以必须得设立两层dp,不断更新即可
if(dp1[i]) dp2[i^k] += dp1[i];
memcpy(dp1,dp2,sizeof(dp2));
AC代码
#include I-Advanced Fruits (lcs,路径记录) HDU - 1503
A big topic of discussion inside the company is “How should the new creations be called?” A mixture between an apple and a pear could be called an apple-pear, of course, but this doesn’t sound very interesting. The boss finally decides to use the shortest string that contains both names of the original fruits as sub-strings as the new name. For instance, “applear” contains “apple” and “pear” (APPLEar and apPlEAR), and there is no shorter string that has the same property.Input
Output
Sample Input
ananas banana
pear peachSample Output
bananas
pearch理解
思路emm 很简单,找到lcs,然后递归输出,相同的如果是lcs内的字符,输出一个即可
书上也是讲过找路径的逆推方式,但第一次手写还是很不熟练,所以记录一下这一道题
AC代码
#include J-Increasing Sequences(双向魔改lis)POJ - 1239
Input
Output
Sample Input
3546
3526
0001
100000101
0Sample Output
35,46
3,5,26
0001
100,000101理解
这题真的好难,自己写的时候一脸懵逼,成功弄出了最后一位最小,但会出现000,1这种情况,然后就懵逼
了,不知道该怎么改,后来看完大佬题解才知道该怎么写
首先,这道题就是lis的魔改版,因为是字符串分段,所以我们可以用以下操作实现题目的要求
(1)原来用于记录lis长度的数组改为记录字符串的下标,来表示分段的情况
(2)正向分段可以找到最后一位最小这种情况
(3)反向分段可以找到第一位最大这种情况
dp公式的话,这边不好表述,直接在代码里面讲好了
AC代码
#include K-XHXJ’s LIS(状压+数位+nlogn lis)HDU - 4352
If you do not know xhxj, then carefully reading the entire description is very important.
As the strongest fighting force in UESTC, xhxj grew up in Jintang, a border town of Chengdu.
Like many god cattles, xhxj has a legendary life:
2010.04, had not yet begun to learn the algorithm, xhxj won the second prize in the university contest. And in this fall, xhxj got one gold medal and one silver medal of regional contest. In the next year’s summer, xhxj was invited to Beijing to attend the astar onsite. A few months later, xhxj got two gold medals and was also qualified for world’s final. However, xhxj was defeated by zhymaoiing in the competition that determined who would go to the world’s final(there is only one team for every university to send to the world’s final) .Now, xhxj is much more stronger than ever,and she will go to the dreaming country to compete in TCO final.
As you see, xhxj always keeps a short hair(reasons unknown), so she looks like a boy( I will not tell you she is actually a lovely girl), wearing yellow T-shirt. When she is not talking, her round face feels very lovely, attracting others to touch her face gently。Unlike God Luo’s, another UESTC god cattle who has cool and noble charm, xhxj is quite approachable, lively, clever. On the other hand,xhxj is very sensitive to the beautiful properties, “this problem has a very good properties”,she always said that after ACing a very hard problem. She often helps in finding solutions, even though she is not good at the problems of that type.
Xhxj loves many games such as,Dota, ocg, mahjong, Starcraft 2, Diablo 3.etc,if you can beat her in any game above, you will get her admire and become a god cattle. She is very concerned with her younger schoolfellows, if she saw someone on a DOTA platform, she would say: “Why do not you go to improve your programming skill”. When she receives sincere compliments from others, she would say modestly: "Please don’t flatter at me.(Please don’t black)."As she will graduate after no more than one year, xhxj also wants to fall in love. However, the man in her dreams has not yet appeared, so she now prefers girls.
Another hobby of xhxj is yy(speculation) some magical problems to discover the special properties. For example, when she see a number, she would think whether the digits of a number are strictly increasing. If you consider the number as a string and can get a longest strictly increasing subsequence the length of which is equal to k, the power of this number is k… It is very simple to determine a single number’s power, but is it also easy to solve this problem with the numbers within an interval? xhxj has a little tired,she want a god cattle to help her solve this problem,the problem is: Determine how many numbers have the power value k in [L,R] in O(1)time.
For the first one to solve this problem,xhxj will upgrade 20 favorability rate。Input
0Output
Sample Input
123 321 2Sample Output
理解
题意真的非常非常简单,问你从L到R中,最长上升子序列为长度为K的数字有多少个,然后看完数据规模,我
自闭了,这真的是我思考加看题解花的最多时间的一道题,也是最难的一道题。所以下面仔细来讲讲这题。
(1)数位dp实现大数字下找解,这里并不难理解,L和R的上限是2^63-1,也就是20位的数位dp差不多就够
了,虽然并没有学过数位dp,但看这题的第一反应还是会想的数位dp的
虽然能想到想到数位dp,但还是有一个难点,如果将数位dp和求上升子序列为K的数字的数量相结合,
显然,因为是数位dp的原因,我们无法对每种情况枚举算上升子序列长度,并且就算能,这么做也必然
会超时。那么就涉及接下来lis nlogn写法和状态压缩相结合的巧妙办法
(2)状压加lis,因为数字的每一位其实只有可能是0到9,那么我们实际上可以用二进制来表示一个上升子
序列每个位置的数字,比如1100000010,就表示当前的最长上升子序列长度为三,且为189,(因为此处采
用的是nlog的lis思想,所以真实情况可能不是一个189的上升子序列,但长度一定是对的),所以,求上升
子序列的长度,也就变成了求二进制中1的个数(非常巧妙的状态压缩)
一些细节放到代码里面阐述
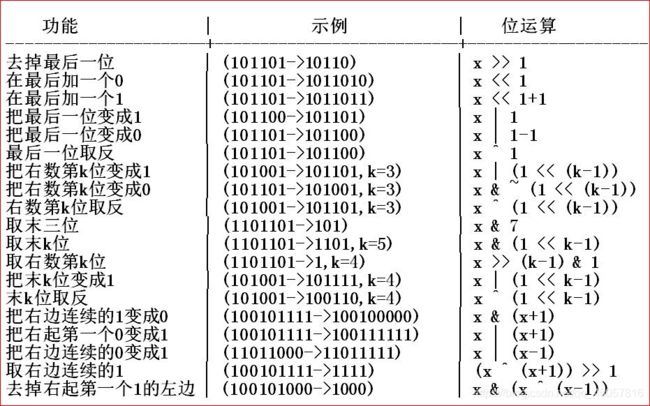
附上一张位运算的操作表,在状压模拟的时候可能会有帮助,也有利于理解后面的代码AC代码
#include L-最大报销额 (预处理01背包) HDU - 1864
Input
m Type_1:price_1 Type_2:price_2 … Type_m:price_m
其中正整数 m 是这张发票上所开物品的件数,Type_i 和 price_i 是第 i 项物品的种类和价值。物品种类用一个大写英文字母表示。当N为0时,全部输入结束,相应的结果不要输出。Output
Sample Input
2 A:23.50 B:100.00
1 C:650.00
3 A:59.99 A:120.00 X:10.00
1200.00 2
2 B:600.00 A:400.00
1 C:200.50
1200.50 3
2 B:600.00 A:400.00
1 C:200.50
1 A:100.00
100.00 0Sample Output
1000.00
1200.50理解
题目看完就可以明白是一个比较简单的01背包,预处理一下就行了
因为背包的下标只能为整数,而题目要求输出2位精度的答案即可,所以我们对背包体积*100处理即可,面额同理
因为是第一道遇到涉及浮点数的背包dp,所以记录一下
AC代码
#include M-Robberies (概率背包) HDU - 2955

For a few months now, Roy has been assessing the security of various banks and the amount of cash they hold. He wants to make a calculated risk, and grab as much money as possible.Input
Bank j contains Mj millions, and the probability of getting caught from robbing it is Pj .Output
0 < T <= 100
0.0 <= P <= 1.0
0 < N <= 100
0 < Mj <= 100
0.0 <= Pj <= 1.0
A bank goes bankrupt if it is robbed, and you may assume that all probabilities are independent as the police have very low funds.Sample Input
0.04 3
1 0.02
2 0.03
3 0.05
0.06 3
2 0.03
2 0.03
3 0.05
0.10 3
1 0.03
2 0.02
3 0.05Sample Output
4
6理解
题目刚看完,第一反应,这和上面的最大报销额差不多啊,无脑敲代码,敲完发现gg
仔细想一想,发现这题思路其实不一样,因为它算的是概率,所以不能做简单加法
转变思路,转为抢n家银行不被抓的概率为多少,根据高中讲过的一点点和概率有关的内容
易得,如果都不被抓,那么概率应该为每次不被抓的概率乘积
而1-每次都不被抓的概率,就能得到每次都被抓到只被抓其中一次的概率
接下来做01背包dp就好了
AC代码
#include N-Least common multiple (数论,分组背包,数据压缩) HDU - 3092
Since the answer can very big,you should give the answer modulo M.Input
Output
Sample Input
Sample Output
理解
这道题虽然涉及到了数论的知识,但感觉不难,知识稍微涉及lcm和gcd而已,众所周知,lcm(a,b) = a*b/gcd(a,b) 想要lcm最大,那么gcd应该等于
1,那么简单易得a和b应该是互质的关系(然后我就简单找质数做了一遍,成功wa)。
下面是互质的数的条件
1.1和任何自然数互质。
2.两个不同的质数互质。
3.一个质数和一个合数,这两个数不是倍数关系时互质。
4.不含相同质因数的两个合数互质。
为了两个数互质,我们可以得出将一个质数n和他的指数倍做同一组,那么所有分出来的数都只要是不同组的,就能保证互质了(自己写的时候疯狂考虑
不全,看了题解才想明白,蒟蒻暴风哭泣),对于含有两个质数的合数,简单想一下,必然会被分成两个质数,所以不用担心(此处@唯一分解定理,写
完这题后面才学到的)
这题还有第二个小问题,因为乘积过大,会爆long long和double,所以emm 采用了取对数的做法压缩数据(直接对原数据取模会影响判断)
本来的dp[j] = dp[j-a]*a 在取对数之后(log(ab) = loga + logb)就变成了 dp[j] = dp[j-a] + loga(此处感谢大佬队友教我)
因为是对数函数的关系,实际上不会应该大小比较,且数据规模压缩后,不用担心溢出问题
AC代码
#include O-Shopping Offers (状态压缩,完全背包) POJ - 1170

In a shop each kind of product has a price. For example, the price of a flower is 2 ICU (Informatics Currency Units) and the price of a vase is 5 ICU. In order to attract more customers, the shop introduces some special offers.
A special offer consists of one or more product items for a reduced price. Examples: three flowers for 5 ICU instead of 6, or two vases together with one flower for 10 ICU instead of 12.
Write a program that calculates the price a customer has to pay for certain items, making optimal use of the special offers. That is, the price should be as low as possible. You are not allowed to add items, even if that would lower the price.
For the prices and offers given above, the (lowest) price for three flowers and two vases is 14 ICU: two vases and one flower for the reduced price of 10 ICU and two flowers for the regular price of 4 ICU.Input
Output
Sample Input
7 3 2
8 2 5
2
1 7 3 5
2 7 1 8 2 10Sample Output
理解
初看这题一脸懵逼,这个背包的费用维度是动态的,这写个锤子啊(当时emm 状压dp还没入门,也没系统学过hash)
后来看完大佬题解,才明白,因为最多只有五种东西买,并且每种东西最多也就买5个,所以可以用6进制压缩(hash的思想)
大概思路就是对于第一件物品1~5,第二件6~30...
用这种方式进行状态压缩,可以巧妙地做到各个费用之间互不干扰
接下来要做的就是把优惠套餐以及单买的价格全都预处理成背包dp内的物品,进行一次完全dp背包dp即可(套餐内可能有非法输入,不能计入)
AC代码
#include (三)其他地方的例题记录
(四)一些收获
关于递推
关于dp
关于分治
(五)感想
1.关于递推公式方面,emm 对于写过的类似题型貌似写起来压力不大?(昆虫繁殖)。也可能是还没遇上真正难的递推题目,本质而言缩小规模慢慢推就好了,然后注意数据规模选择循环递推还是递归,或者是高精度之类的(蜜蜂路线),或者说是打表or记忆化搜索,这些都是小细节,关键还是dp公式怎么推(话说写dp公式好费纸,画画表一页纸就没了。。。)
所以emm 加油抽时间补数据结构的内容吧(狗头)