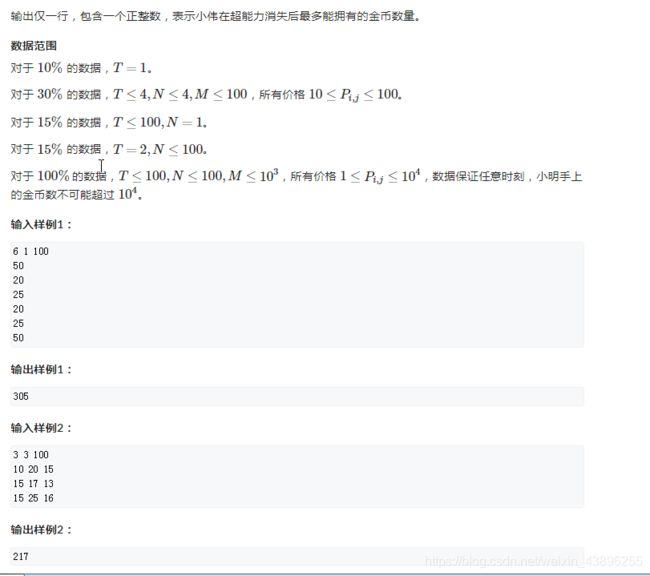
2019NOIP普及组题解

1161. 数字游戏

原题链接
分析: 一个签到题，题意很明确，给一个字符串，判断字符串里面有多少个1，直接遍历一遍输出结果。
时间复杂度:O(n)。
AC代码:

#include
#include
#include

using namespace std;

int main(){
    string s;
    cin>>s;
    int res = 0;
    for(int i = 0;i<s.size();i++){
        if(s[i] == '1')
          res++;
    }
    cout<<res<<endl;
    return 0;
}

1162. 公交换乘


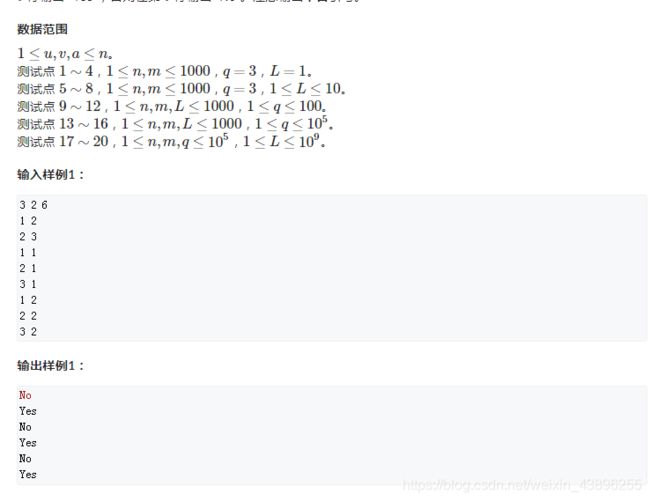
原题链接
分析:一道较为简单的模拟题，题意大概就是小明每坐一次地铁，就会获得一张与地铁等票价的优惠券，在下次乘坐公交车的时候，如果手里的优惠券价格大于等于公交车的价格，并且乘坐公交车的时间减去乘坐地铁的时间大于等于45min，那么他就可以白嫖 免费乘坐，并且题意已经明确指出，只能按从早到晚获得的优惠券使用，这样一来，就不用考虑优化的问题了。
  现在要考虑的问题就是该怎么样来存储小明手里的票，我们很容易可以想到队列这种数据结构，还有就是需要存储哪些数据信息，根据题意，我们可以知道有票价，乘车时间，那么就可以使用结构体数组来充当一张一张的票，里面有两个变量,票价跟乘车时间，再外加一个变量，来标注这张票是否被使用过。

struct Queue{
   ll price,time;
   bool used;
}tickt[N];

  接下来要思考的问题就是该怎么样去模拟，我们可以遍历一遍输入的数据，同时定义一个变量，res来存放最终的票价，如果遇到地铁票，就把票价加到最终结果上，如果遇到公交车票，就在手里找，看看有没有符合条件的优惠券，如果没有，就把这张公交车票的票价也加到最后的结果上，如果有，就使用，与此同时把used变量置为true。
注意:我们必须时刻维护队列里的票，即清空掉再也用不到的票，因为一张票的有效期最多保持45分钟，所以手里的票一定不会超过45张，这样会降低时间复杂度
时间复杂度O(n*45)

AC代码:

#include
#include
#include
#define N 100010
typedef long long ll;
using namespace std;

struct Queue{
   ll price,time;
   bool used;
}tickt[N]; //定义票的结构体数组

ll res = 0,l,r;

int main()
{
    ll n;
    cin>>n;
    l = r = 1; //定义队列的队头跟队尾指针，这里采用静态数组来模拟队列，就不使用STL模板了
    for(ll i = 1;i<=n;i++){
        ll type,price,time;
        cin>>type>>price>>time;  //读取当前的票的类型，时间，票价
        if(type == 1){   //如果是公交车票的话
            while(l<r && (time-tickt[l].time)>45) l++;  //一个优化，也是一个坑点，我们需要及时的把手里已经超时的优惠券清空掉，如果不清空的话，在一定的情况下时间复杂度会退化到O(n^2)
            ll k;
            bool success = false;  //定义一个变量来表示是否成功的找到了一张符合条件的优惠券
            for(k = l;k<r;k++){
                if(tickt[k].used == false && tickt[k].price>=price)
                    {
                      tickt[k].used = true;  
                      success = true;
                      break;  
                    }
            }
          if(!success) res+=price; //如果没有找到，就得买票了
        }else{  //如果是地铁票的话
            res+=price; //直接买票
            tickt[r++] = {price,time,false}; //把获得的优惠券加入到当前队列中去
        }
        
    }
    cout<<res<<endl;
    
    
    return 0;
}

1163. 纪念品


原题链接

分析:一道鬼畜dp题目，看到这道题，我们可以联想到张新华的《算法竞赛宝典》第二部上面的股票买卖问题，与这个题较为相似，读完题目，相信很多人都是一脸懵逼，只是大概知道用dp做，但是没有具体的思路，我的解题思路也是来自于yxc大佬。
  思路: 因为可以在第a天买入，第b天卖出，当然，b要大于等于a。这样收入就是price[b]-price[a] （我们假设用price数组来存储某个物品第i天的物品的价格）,但是再去换个角度思考这个问题呢，我们假设一个人在第a天买入一个物品，第a+1天卖出这个物品，然后又买回来，在第a+2天又卖出去，当天再买回来…一直到第b天卖出去，不难发现，这样其实是跟在第a天买入，第b天卖出的效果是一样的,那么经过这样的转换有什么好处呢，一个好处就是我们把思考的范围缩小了，原来需要考虑好几天，现在我们只需要考虑怎么样才能保证今天买入在明天卖出的时候可以获利最大就好了，也就是说，我们只需要考虑隔一天获利最大就好了。思考到这一步，这道题目就完成了三分之一了。
  接下来要考虑的一个问题就是，怎么样保证隔一天可以获得的利润最大化，不难发现，这其实就是我们在dp入门的时候最简单的母版问题————完全背包问题。如果有不懂的小伙伴，可以去看这篇博客https://blog.csdn.net/m0_37809890/article/details/83153974
现在，我们要做的就是套母版，我们手里拥有的钱就是背包容量，针对每一个物品，我们可以买好多个，每买一个就需要耗费相应的钱，也就是相当于占据了背包容量，获得的价值就是第二天的价格减去第一天的价格。这样就可以得到第二天的最大利益，一共有n天，我们只需要做n-1次完全背包问题就可以了。

时间复杂度:O(TNM)

AC代码:

#include
#include
#include
#include
#define N  100010
typedef long long ll;

using namespace std;

ll t,n,m;
ll f[N]; //f数组来存储最大获利
ll price[101][N]; //用price数组来存储第i个物品第j天的时候的价格

int main(){
    cin>>t>>n>>m;
    for(int i = 1;i<=t;i++)
      for(int j = 1;j<=n;j++)
         cin>>price[i][j];  //读取数据
    for(int i = 1;i<t;i++){ //做n-1次完全背包问题
        memset(f,0,sizeof(f));  //每次做之前初始化f数组
         for(int j = 1;j<=n;j++)  //完全背包问题母版
            for(int k = price[i][j];k<=m;k++){
                 f[k] = max(f[k],f[k-price[i][j]]+price[i+1][j]-price[i][j]);
            }
        m+=f[m];  //做完一次后加到现有的金币数上
    }
    cout<<m<<endl;
    return 0;
}

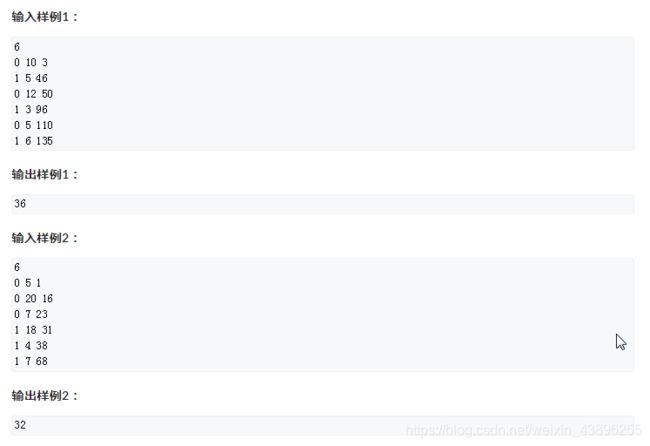
1164. 加工零件


原题链接

分析:这道题目理解起来还是比较费劲的，题目大意就是说，如果一个人想生产一个L阶段的零件，那么与他相连的所有点必须都生产一个L-1阶段的零件给他，现在题目已知某一个点想要生产一个L阶段的零件，询问一号点是否需要提供原材料。
  首先，这道题目肯定是图论里面的题目，这没跑了，我们知道图论入门的时候学的就是dfs，bfs，地杰斯特拉，弗洛伊德，SPFA等等这几种算法，还有什么最小割，网络流之类的，要想知道该题目是否能用得上这些母版算法，我们还是得建立该题目的模型。

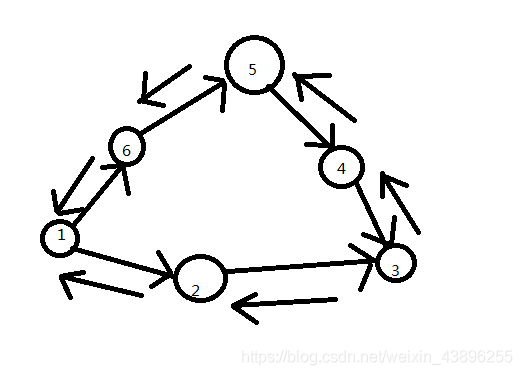
我们先来看一个图，现在比如3号点，想要生产一个L = 2 阶段的零件，那么2号点必须给他一个1阶段的，1号点必须给2号点原材料。
如果3号点想要生产一个4阶段的呢，那么2号点必须生产3阶段的，3号点必须生产2阶段的…这就又回到了上一个问题，我们总结可以得到，如果一个点跟一号点之间的最短偶数距离为L，那么如果这个点生产L+2，L+4，L+6…阶段的零件时，一号点必须提供给原材料。
同理，一个点跟一号点之间的最短奇数距离也有这个推论成立…
现在我们来总结一下，我们用两个数组来存储一个点到一号点之间的最短距离，一个存储最短奇数距离，一个存储最短偶数距离。
当询问的时候，我们就去查询这两个数组，如果是奇数，就去查询存放奇数最短距离的数组，如果是偶数就去查询存放最短偶数距离的数组。
至于怎么求最短路，方法就很多了，可以狄杰斯特拉，SPFA，bfs。我在这里就提供一种较为简单的bfs算法。

时间复杂度:O(n)

AC代码：

#include
#include
#include
#include
#include
#include
#define N 100010
using namespace std;

int ji[N],ou[N];
vector<int> v[N];
int n,m,q;


void bfs(){
    memset(ji,0x3f,sizeof(ji));//奇数最短路径
    memset(ou,0x3f,sizeof(ou));//偶数最短路径
    queue<pair<int,int> >q;
    for(int i=0;i<v[1].size();i++){
        ji[v[1][i]]=1;
        q.push(make_pair(v[1][i],1));
    }
    while(q.size()){
        int x=q.front().first,y=q.front().second;
        for(int i=0;i<v[x].size();i++){
            if(y%2==1){//奇数+1=偶数
                if(y+1<ou[v[x][i]]){
                    ou[v[x][i]]=y+1;
                    q.push(make_pair(v[x][i],y+1));
                }
            }else{//偶数+1=奇数
                if(y+1<ji[v[x][i]]){
                    ji[v[x][i]]=y+1;
                    q.push(make_pair(v[x][i],y+1));
                }
            }
        }
        q.pop();
    }
}



int main()
{
    cin>>n>>m>>q;
    for(int i = 1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        v[x].push_back(y); //采用邻接矩阵来存储图
        v[y].push_back(x);
    }
    bfs();  //跑一遍bfs得到答案
    while(q--){
        int a,l;
        cin>>a>>l;
        if(l%2 == 0){
            if(ou[a]>l) puts("No");
            else puts("Yes");
        }else{
            if(ji[a]>l) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}