菜鸡备战机试刷题实战1
菜鸡备战机试刷题实战1
2019.7.11
这次刷的题是我在华师大的夏令营机试题里最简单的一道,题目挺有趣,是我人生中第一次接触的机试,也是我半吊子c++刚开始学的第3天做的题目。
(我们专业只教了Java,还主要运用与工程训练中,在得知夏令营入营之后才意识到要备战机试,但是一直被期末考试和大作业拖着没机会开始)
之所以决定用c++做机试题而不用java,一是因为java的运算时间普遍是c++的几倍,容易超时;二是因为c++也可以用c的语法,即向下兼容;三是因为c++的STL模板库很好用。
(做题过程中除了《算法笔记》之外,还一直有一个很牛的学长进行指导,所以过程才如此顺利,但是好久不回顾我就会忘记,所以想到了用做题日志把思路和细节给记录下来)
关键词
错位排列,递推公式
题目链接
https://acm.ecnu.edu.cn/contest/186/problem/F/
(只有参加了夏令营的账号可以进入此链接,所以题目贴到了下边)
题目详情
F. 小啵的抽奖
单点时限: 1.0 sec
内存限制: 512 MB
小啵邀请了 N (1≤N≤20) 位同学来参加他的抽奖活动。
每位同学都有一个抽奖券,他们只需要在抽奖券上写下自己的名字,然后扔进抽奖箱中。
接着,小啵会随机给每位同学发 一个 抽奖券,如果一位同学拿到了写有自己名字的抽奖券,那么他就中奖了。
小啵的问题是,他有多大的概率不用准备任何奖品?(也就是说,没有任何人中奖)
答案以百分比形式给出,保留到小数点后两位。
输入格式
第一行输入一个整数 Q ,表示有 Q 轮抽奖。
接下来 Q 行,每行输入一个整数 N ,表示这一轮抽奖的人数。
输出格式
输出 Q 行,每行一个百分比数,表示没有人中奖的概率
思路整理
错位排列(每个位置上都不是原来的数),递推(可以参考斐波那契数列的递推方法)
- 概率=错位排列的个数/总排列的个数
- 分母→总排列的个数:N个数的全排列→N!
- 分子→使用递推
设n个数的错位排列个数是f(n),f(n-1)或者f(n-2)等计算得到
假设已经算出来n-1个数的错位排列个数,即已经得到了f(n-1)
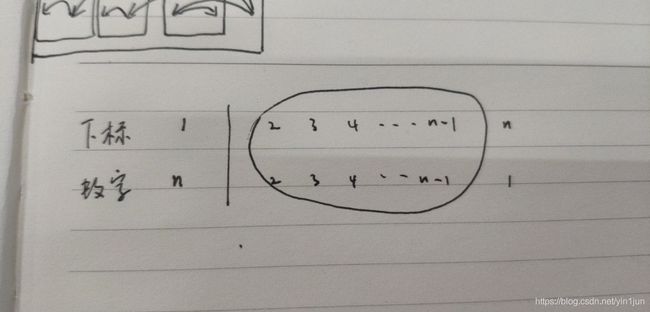
为了实现错位排列,n只能放在1n-1的位置上,假设n放在位置1上,那么1n-1就要放在位置2~n上。
n个数的排列分为两种情况:
- 1放在位置n上,则2(n-1)就要放在位置2(n-1)上,一共是n-2个数进行错位排列,已知n个数错位排列个数为f(n),这种情况个数为f(n-2)
- 1不在位置n上,而2~(n-1)也不能在自己的位置,就等价于第一种情况,也就是n-1个数进行错位排列,这种情况个数为f(n-1)。所以一共是f(n-2)+ f(n-1)种
n的位置有多种可能,n在每个位置等价,所以对于n个数来说有n-1种可能
则f(n)=(n-1)*( f(n-2)+ f(n-1))
错位排列的情况:f(1)=0, f(2)=1, f(3)就可由此推出,如此就能知道分子
阶乘也可以用错位排列写出来
第一次磕磕绊绊完成的程序,虽然可以跑到满分,但是存在的排版和优化问题还是很大的,代码如下:
#include
typedef long long LL;
int main(){
int T;
scanf("%d", &T);
while (T--){
//double n,t;
LL n;
LL f[30] = { 0, 0, 1 };
LL fac[30] = { 1,1,2 };
LL ans = 1;
scanf("%lld", &n);
if (n <= 20 || n >= 1){
//f(n)=(n-1)(f(n-1)+f(n-2))
for (LL i = 3; i <= n; i++){
f[i] = (i - 1)*(f[i - 1] + f[i - 2]);
//ans *= j;
}
for (LL j = 1; j <= n; j++){
fac[j] = j * fac[j-1];
}
//printf("%.2f\n", fac[n]);
double t =100* (double)f[n] / (double)fac[n];
printf("%.2f%%\n", t);
}
else{
printf("0.00%");
}
}
return 0;
}
改正版如下:
#include
using namespace std;
typedef long long LL;
LL p[30] = {1, 1, 2};
LL a[30] = {0, 0, 1};
int main() {
for (int i = 3; i < 30; ++i) {
p[i] = p[i - 1] * (LL)i;
a[i] = (LL)(i - 1) * (a[i - 1] + a[i - 2]);
}
int T;
scanf("%d", &T);
while (T--) {
int n;
scanf("%d", &n);
double res = (double)a[n] / p[n] * 100.0;
printf("%.2f%%\n", res);
}
return 0;
}
可以明显地看到,代码风格简洁了许多,其中需要注意的是运算符号前后使用空格,以及对于long long型预先定义好,如下:
typedef long long LL;
机试的oj中应该也可以用到万能头文件,这个还是很好用的,以防止想不起来而犯错:
#include
using namespace std;
还有尽量使用scanf和printf进行输入输出,比cin和cout的速度要快很多(虽然我自己也没搞太清楚,但是这么做总没错的,因为一些oj会用大数来卡分数)。
同时如果两个人交流代码的话,一个网址也很不错,有多种格式可供选择,可以还原代码的格式,并且避免了文件传输的麻烦:
https://paste.ubuntu.com/
这样差不多第一天的练习就结束了,但是对于第一题的拓展还未结束。
2019.7.12
关键词
打表(在昨天的基础上)
思路整理
之前只听说过打表这个名词,但是一直不了解是什么意思,这个题目也可以用打表的办法做,这样就可以避免存在大数而超时,因为当时研究了一会儿,所以先贴上学长的代码,被注释的就是打表的语句:
#include
using namespace std;
typedef long long LL;
LL p[30] = {1, 1, 2};
LL a[30] = {0, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961, 14684570, 176214841};
int b[30];
int main() {
for (int i = 3; i < 30; ++i) {
p[i] = p[i - 1] * (LL)i;
}
/**************************************************
for (int n = 3; n <= 20; ++n) {
for (int i = 1; i <= n; ++i) {
b[i] = i;
}
int cnt = 0;
do {
int flag = 1;
for (int i = 1; i <= n; ++i) {
if (b[i] == i) {
flag = 0;
break;
}
}
cnt += flag;
} while (next_permutation(b + 1, b + n + 1));
a[n] = cnt;
printf("%d, ", cnt);
}
**************************************************/
int T;
scanf("%d", &T);
while (T--) {
int n;
scanf("%d", &n);
if (n > 12)
n = 12;
double res = (double)a[n] / p[n] * 100.0;
printf("%.2f%%\n", res);
}
return 0;
}
利用注释这部分,c++有个函数叫next_permutation,可以按照字典序从小到大枚举下一个数组。所以看看所有排列符不符合,统计一下即可。但是最多只能跑到12个左右,再多跑不动了,太慢了。然后把n<=12的结果直接放在数组里,这部分打表的代码注释掉。巧的是,这题n>12以后的答案全部相同。所以这道题直接过,也就意味着打表就可以拿到满分。
C++的next_permutation函数:传入两个参数,一个是数组首地址,一个是尾地址,它会把数组变成下一个字典序更大的排列
所以一开始数组里放123456,字典序最小的
调用一次next_permutation(a, a + n),它就变成下一个排列了,并且返回True,说明有下一个排列
字典序:两个数组比大小,从第一个开始比,如果一样就比下一个,直到第一个不一样的,谁大,谁的字典序就大。比如两个字符串,fsdfsad和fsda,就是是前一个大。
所以枚举全排列,就是初始化为最小的1,2,3,4,…,n,然后调用库函数,一次次变大,直到不能变为止,也就是n,…,3,2,1
那对于每一个排列,是不是错位排列,就直接看每个位置等不等于原来的数就行,比如第6个位置,如果是6,那这个排列就不对,不计数。也就是使用暴力枚举的办法。
枚举全排列一般就用do while。
差不多这些就是第二天的心得,对于菜鸡来说,每一个大佬们烂熟于心的知识点都是新世界,所以虽然思考过程存在阻碍,但是也充满了乐趣。(其实第二天也不是太清楚打表是啥,所以主要还是了解了next_permutation函数,并没有动手去写,因为写了也没结果)
2019.7.13
关键词
打表
思路整理
n=1,2可以口算出来,所以要计算3~20的情况,使用for循环,对于每个n,枚举它的排列,对于每个排列要判断它是不是错位排列,如果是,就对count+1,如果不是,就不用管,然后所有排列枚举完了,得到的count就是n个元素的错位排列数量,保存到f[]里即可。再设置一个变量flag,初始化为1,用作记录,如果有位置相等了,flag=0,说明这个排列就错了,直接break。
while (next_permutation(b+1, b+1+n))
这个语句,这样b1到bn就会变成下一个排列,这个函数返回true说明有下一个排列,等到b数组变成降序的,那这个next就返回false了,就不会进行下一次do了。
我自己理解之后写的打表函数如下,其中被//注释的部分就是打表之后运行的结果:
#include
#include
//#include
using namespace std;
typedef long long LL;
//LL f[30] = { 0, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961, 14684570, 176214841, 2290792932, 32071101049, 481066515734, 7697064251745, 130850092279664, 2355301661033953, 44750731559645106};
LL f[30] = { 0, 0, 1 };
LL fac[30] = { 1, 1, 2};
LL b[30];
int main() {
/*
for (LL i = 3; i <= 30; i++){
f[i] = (i - 1)*(f[i - 1] + f[i - 2]);
fac[i] = i * fac[i - 1];
}
int T;
scanf("%d" , &T);
while (T--) {
LL n;
scanf("%lld" , &n);
double t =100* (double)f[n] / (double)fac[n];
printf("%.2f%%\n", t);
}
*/
for (int i = 3; i < 30; i++) {
for (int j = 1; j <= i; j++) {
b[j] = j;
}
int count = 0;
do {
int flag = 1;
for (int k = 1; k <= i; k++) {
if (k == b[k]) {
flag = 0;
break;
}
}
count += flag;
} while (next_permutation(b + 1, b + i + 1) == true);
f[i] = count;
printf("%d, ", count);
}
return 0;
}
这样第三天也就是蛮有收获的,因为练机试光看不行,还是要自己动手给跑通。
三天写完第一题,菜鸡流下了感动的泪水。