计算几何入门 1.3：凸包的构造——增量构造法

极点法和极边法的复杂度分别为O(n^4)和O(n^3)，当点集S的规模稍大时就难以适用了。为了满足实际需要必须寻找更高效的算法来构造凸包。

一、减治

在引入新算法之前首先来回顾一下经典的算法思想：减治（decrease and conquer），注意不是分治（divided and conquer），二者稍有区别。简单来讲就是将问题划分为一个个简单的小问题，减而治之，逐个求解，最终就能得到整个问题的解。

 

减治法的经典例子就是插入排序（insertion sort）。插入排序的过程可以归结成下图：

排序的过程中将序列分为两部分：已排序部分（sorted）和未排序部分（unsorted）。每次排序都是从unsorted中拿出一个元素，通过一次顺序查找过程在sorted部分中找到位置并插入其中。

 

整个插入排序的过程就是逐个元素的去“蚕食”unsorted部分的过程，连续的进行这个操作就会将整个问题解决。这种将大问题分解成小问题的减治过程，又被看成一种递增的、增量式的策略（incremental strategy）。这种思想为解决凸包问题提供了新的思路：从逐个插入新点的角度构造凸包。

 

典型流程如下图（标识为：极点/整体规模）：

插入新的点可能的情况有：新点对凸包有“贡献”，例如5/5→6/6，6/6→7/7；新点也有可能没有“贡献”，例如7/7→7/8；还有可能使原先有“贡献”的点失效，极点数量减少，例如7/8→6/9。那么如何对不同情况进行处理呢？
 

二、in-convex-polygon test

构造过程的核心算法应该是：判定待定点是否位于某多边形内部（in-convex-polygon test）。再看上图流程，实际上每步的核心就是判断点位于多边形内部还是外部，若落在外部，则新插入的点就是下一个极点，否则舍弃。

 

考虑基本情况，给定一个点和一个多边形，如何高效判断该点与多边形的位置关系呢？

 

一种思路是：我们可以先对多边形进行一个“预处理”，给每个点按序编号，类比有序向量二分查找的思想，来逐步缩小规模。如下图：

首先任选一点为基准点（蓝色点），然后用二分法选取其余点的“中点“（预处理已经为所有点排了序），然后判断基准点到终点的有向直线与待定点的位置关系（to-left test）。然后可将搜索范围减半，反复上述过程，直到最后退化为平凡情况：三角形与点的位置关系（in-triangle test）。

 

分析一下算法的整体复杂度：整个算法共log(n)步，每步的to-left test或in-triangle test都为常数成本，则整体复杂度为log(n)。至此，我们似乎得到了一个log(n)的“高效”算法，但是这种方法真的可行吗？

 

注意，每步都会将原凸包规模减半，也就是说凸包是动态的，随时可能变化。这种方法和极点法或极边法中静态查找的情况是完全不同的。

 

类比插入排序的过程来解释这个问题。为何插入排序的复杂度是n^2而非nlog(n)？每次插入时，既然sorted部分已经有序，为何不使用二分查找来取代顺序查找（复杂度由n变为log(n)）？这不得不考虑sorted部分的动态性，每次插入后它的结构都会改变，而二分查找必须在静态结构中实现。当然可以使用std::vector这类支持按秩访问（call by rank）的数据结构，但是插入时维护vector的成本依旧是线性复杂度。因此插入排序的总体复杂度是n^2。要处理的凸包与插入排序中sorted部分本质是一样的，它们都不是静态不变的结构，而要随着算法执行而不断变化。若要每次在log(n)成本下完成待定点的in-convex-polygon test，必须将凸包存储为类似vector的数据结构，但是每次向这种数据结构插入新点的成本依旧是线性的。因此对凸包进行的所谓“预处理”是没有意义的，这种减治策略算法复杂度最低应该为O(n^2)。

 

到现在问题依旧没有解决，究竟如何用这种增量式的策略来构造凸包？其实复杂问题中最朴素、最基本的方法反而是最有效的。

 

in-convex-polygon test最基本的方法是什么？就是按一定方向（约定为逆时针）凸包的每条边和待定点做to-left test，一旦有一次test为false就能断定点在凸包外面。这实际上就是将in-triangle test推广多边形的情况。因此每次in-convex-polygon test的成本就会变成当前凸包的规模，也就是n，对于每个新点做一次in-convex-polygon test，构造算法的整体复杂度就是O(n^2)。算法的复杂度从极边法的O(n^3)又下降了一个数量级。

 

三、 support-line

整个构造算法可以分成两大部分：

• 如何判断凸包与新点的位置关系（in-convex-polygon test）
• 如何向凸包插入新点

上述方法已经将第一个问题解决了，剩下的就是如何插入新点的问题。考虑以下典型情况：

新点位于原凸包外部，如何将新点插入得到新凸包？直觉判断应该是如下连接方法：

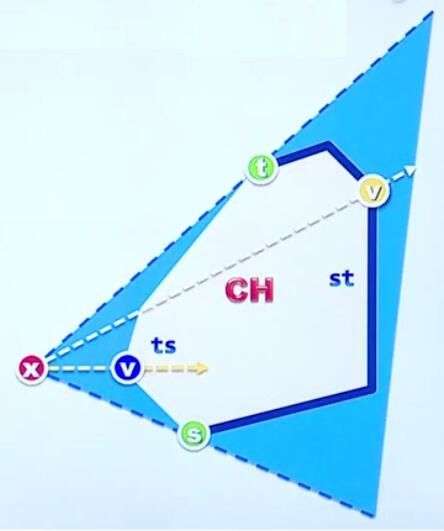
将新点x插入原凸包的过程，本质上就是寻找两个连接点s和t，将x和t、s分别连接得到新的凸包。注意t和s两点将整个原凸包边界分为两部分：st和ts两个有向段。构造新凸包就要保留远端st、舍弃近端ts。取代近端ts的两条线就是x和t的连线xt和xs，被称为切线（tangent）或者support line。

 

t、s二点的查找就成了问题的关键。

 

我们在凸包上任取一点v，按逆时针方向v点会有一个直接前驱点和直接后继点。考察有向直线xv与点v直接前驱和直接后继的位置关系（两次to left test），记录为一个pattern表。

结果无非是四种情况：v的直接前驱和直接后继相对于有向直线xv的位置是RL，LR，LL，RR。例如上图黄色点v，是R和L；蓝色点v分别是L和R。实际上凸包边界st上所有点的pattern都为RL，ts上所有点的pattern都为LR。关键点在于：点S的pattern是LL，点t的pattern为RR。

 

因此对凸包边界每个点做两次to left test，判断其pattern就可找出s和t，花费时间成本为常数。

 

四、incremental construction

再来回顾整个凸包构造算法的两大问题：in-convex-polygon test和插入新点。分开考虑只是为了将思路简化，实际上这两个问题可以套用一个算法，同时来解决。

 

具体做法就是，对于每个待定点x，不必特意去考虑它与凸包的位置关系，而是遍历凸包上每一个点。对于凸包边界上的每一个点，我们都能通过两次to left test迅速判断出pattern。

 

对于x位于凸包外部的情况，经过遍历凸包的点，我们很容易就能得到s和t的位置，得到两条support line，从而构造出新的凸包；而对于x位于凸包内部的情况，凸包边界每个点都不可能出现RR或LL的情况，直接舍弃x即可。

 

每次遍历凸包边界点的复杂度为O(n)，整个构造过程要增量式的逐点考察，自然得到了一个O(n^2)的incremental construction算法。

 

这就是所谓增量构造法来构造凸包的过程。构造过程巧妙的避开了特殊处理诸如5/5→6/6、7/7→7/8、7/8→6/9等复杂情况，采用一致的思路逐个考察“新点”，最终完成凸包的构造。

 

本文是学堂在线课程《计算几何》的笔记，帮助理解和记录思考过程，不够严谨请见谅。