2019年CS224N课程笔记-Lecture 14: Transformers and Self-Attention

资源链接：https://www.bilibili.com/video/BV1r4411

（np带个妹子让课堂不尴尬～）

正课内容

可变长数据的表示，也就是序列学习的基本使用组件，主要包括神经机器翻译，摘要，问答等项目

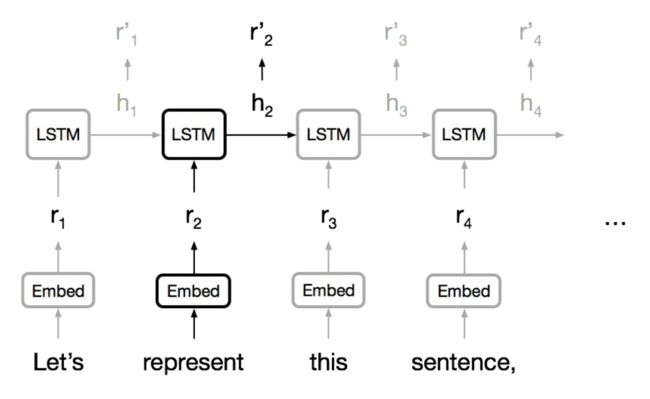
通常使用 RNN 学习变长的表示：RNN 本身适合句子和像素序列，LSTMs, GRUs 和其变体在循环神经网络模型中占主导地位。

但是序列计算抑制了并行化（RNN也是这个缺点），没有对长期和短期依赖关系进行显式建模。
我们想要对层次结构建模，RNNs(顺序结构)看起来很浪费！

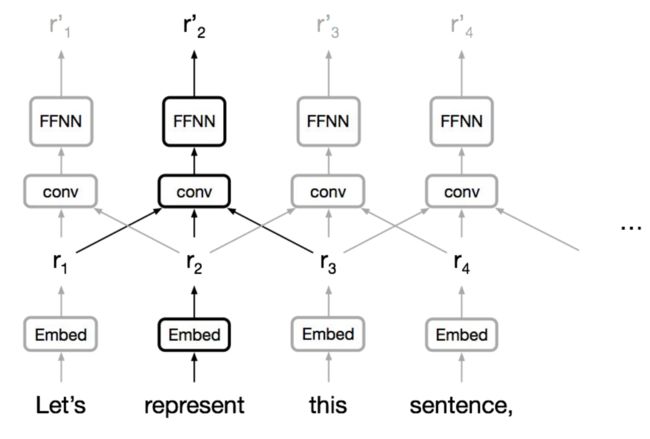
卷积神经网络

层次上并行化很简单，利用局部依赖，不同位置的交互距离是线性或是对数的，远程依赖需要多层（讲的有点快 没怎么听懂555555）

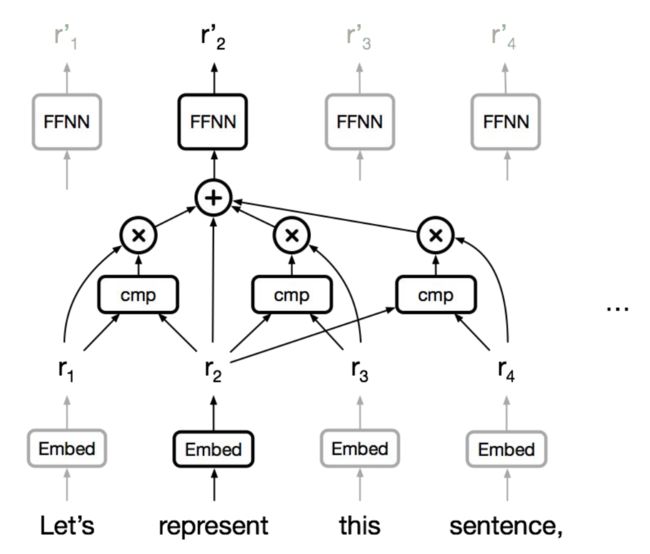
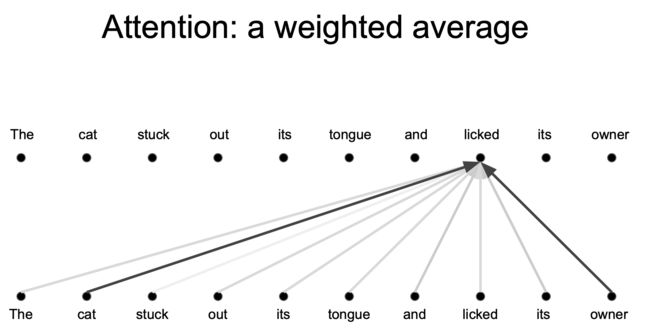
注意力

NMT 中，编码器和解码器之间的 Attention 是至关重要的，那么为什么不把注意力用于表示呢？

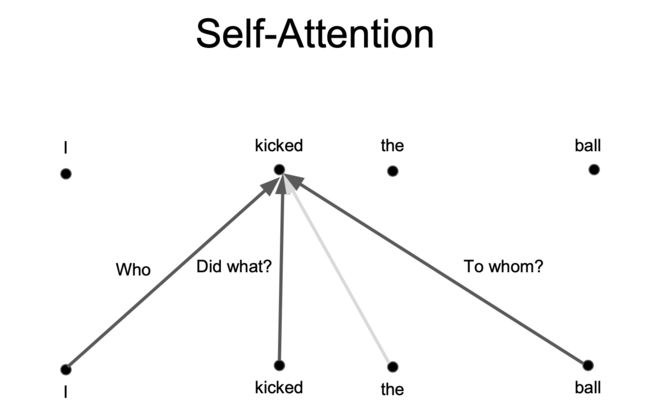
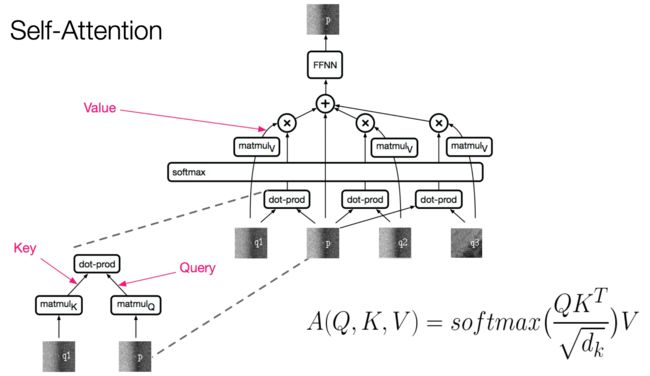
Self-Attention

任何两个位置之间的路径长度都是常数级别的，门控 / 乘法 的交互，可以并行化（每层）
可以完全替代序列计算吗？基本CNN在序列任务上注意力都可以实现，对于RNN也是有很多优点，完全替代不至于吧，但是已经非常有优势了～

Text generation/文本生成

以前的工作

自我注意力分类与回归：

Parikh et al. (2016), Lin et al. (2016)

RNNs自我注意力：

Long et al. (2016), Shao, Gows et al. (2017)

循环注意力：

Sukhbaatar et al. (2015)

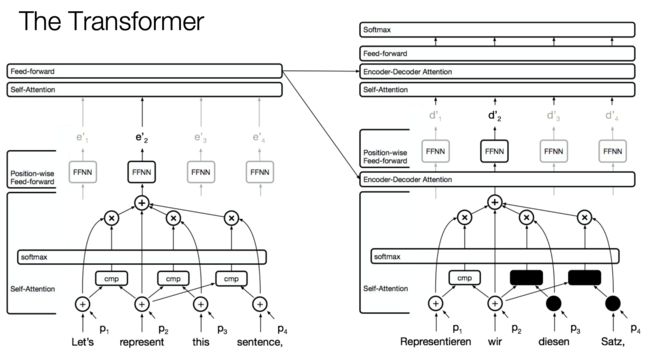
The Transformer

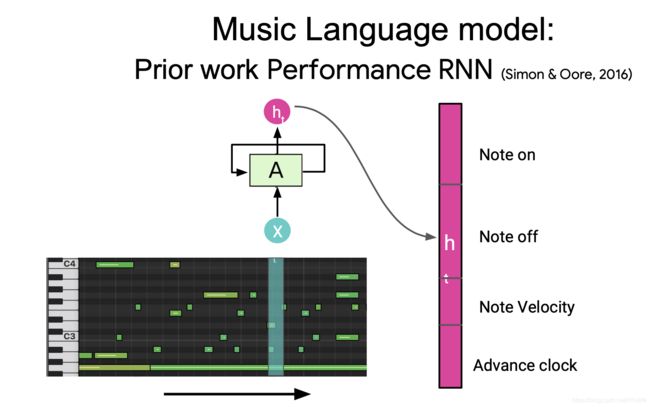
我们主要是用注意力关注计算表示的输入，想象一下在英语德语翻译中，我们有我们的话，注意力的排序是不变的，所以我们只需要改变自己的位置，它不会影响我们的输出，所以我们往其中添加位置表示。（说实话没怎么听懂，也可能是翻译的不太准确的原因）

在编码器方面，我们有一个自我注意力层，只是重新计算表示，对于每个位置同时使用注意力，然后我们有一个前反馈层也有残差连接。每一层输入都会有一个残余连接，只是需要激活

在解码器上，我们使用自我注意力来模仿语言模型，并且使用自我注意力来模仿语言模型的方式是增强通过掩盖你可以看到的位置的因果关系，所以基本上，第一个位置是不能往前看的/这是非法的，

（说实话听着有点懵～这里等我把这个课程都过完后，自己去详细查阅不懂的地方再回来补充吧～）

各类模型的复杂度

由于计算只涉及到两个矩阵乘法，所以是序列长度的平方，当维度比长度大得多的时候，非常有效

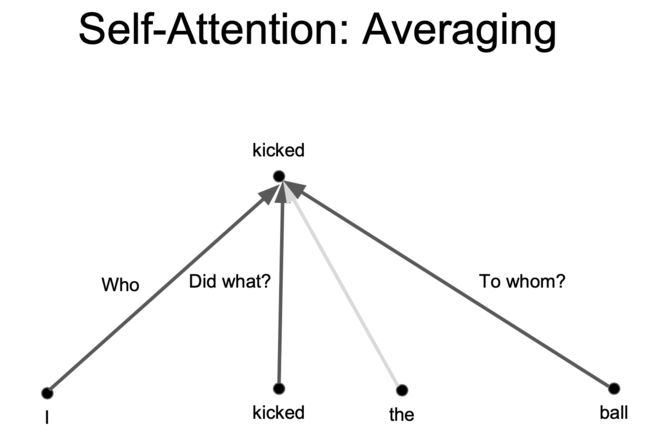
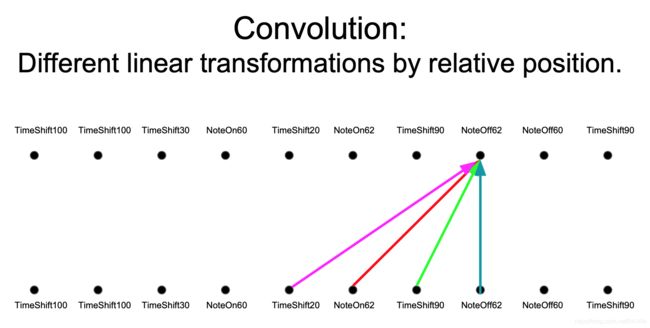
卷积和自我注意力的对比

上例中，我们想要知道谁对谁做了什么，通过卷积中的多个卷积核的不同的线性操作（不同的线代表卷积出不同的信息），我们可以分别获取到 who, Did what？, To whom？ 的信息。

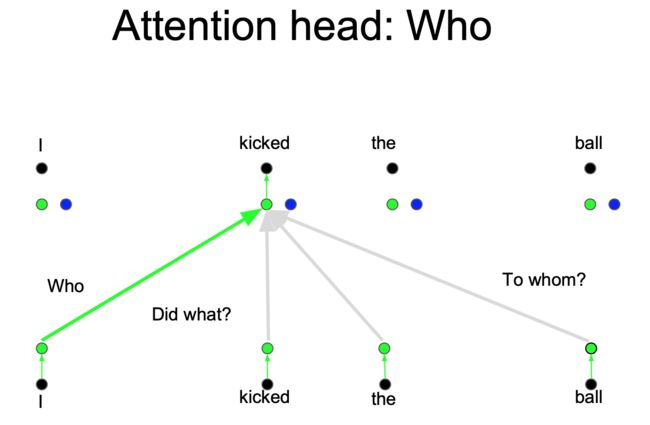
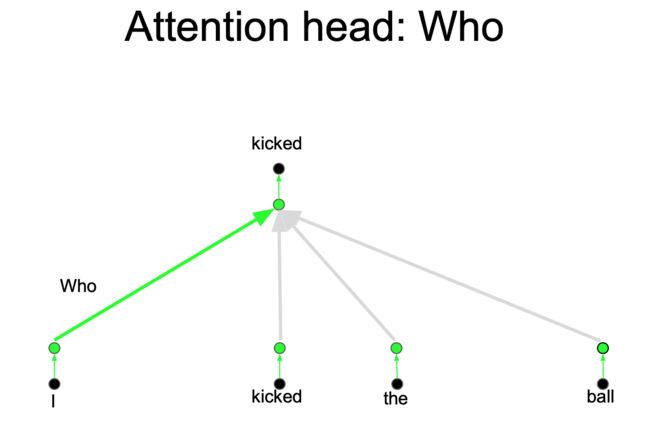
但是对于 Attention 而言，如果只有一个Attention layer，那么对于一句话里的每个词都是同样的线性变换，不能够做到在不同的位置提取不同的信息（所以需要加位置信息），这就是多头注意力的来源，灵感来源于 CNN 中的多个卷积核的设计

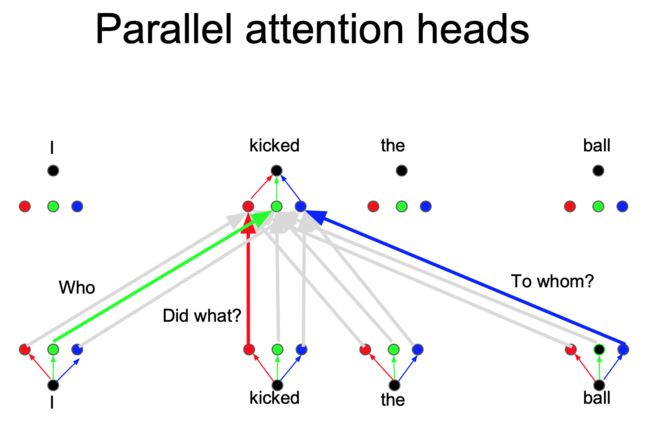
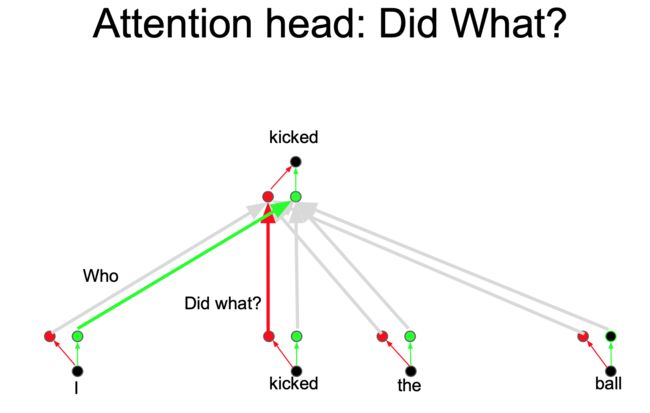
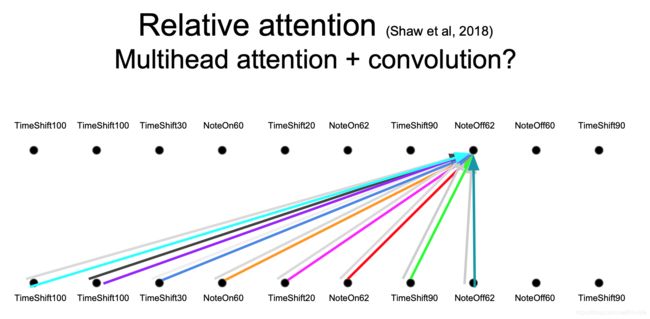
一层注意力的时候明显不足的，也就是把注意力层当成特征探测器，一个颜色可以探测一个问题，Who, Did What, To Whom 分别拥有注意力头（如下图所示），而且（注意力头/上述不同颜色的线）还可以并行计算，这样就可以模拟一个卷积了。为了效率，减少注意力头的维度，并行操作这些注意力层，弥补了计算差距

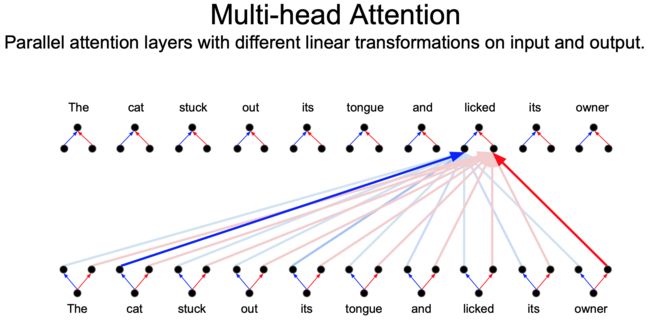
相对位置的不同线性变换（这个图好像没说，但是这句话说过，应该就是该图内容）

在输入和输出上具有不同线性变换的平行注意层（这个图好像没说，但是这句话说过，应该就是该图内容）

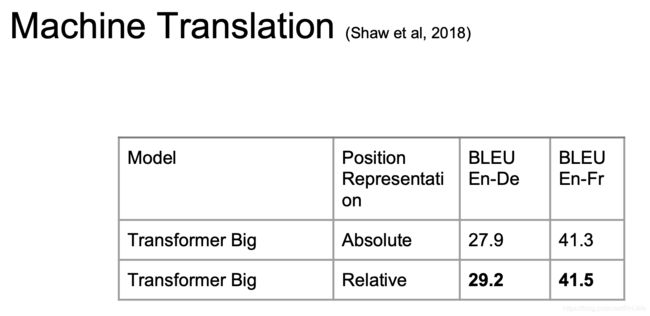
当我们把它应用到机器翻译的时候，效果非常不错

但我们并不一定比 LSTM 取得了更好的表示（理论上LSTM可以模拟任何函数），只是Translation更适合 SGD/随机梯度下降，可以更好的训练，我们可以对任意两个词之间构建连接

很多工作是在tensor2tensor中推出的，随着JAX的到来未来可能发生变化，一个来自亚马逊的框架Sockeye等有很多好的序列到序列模型（不知道是否有Translation）

残差连接的重要性

（这个之前我们就知道残差连接很重要了，例如缓解梯度消失、支持更深的模型等～）

如果我们切断了残差连接，注意力分布如上图中中间的图一样，事实上它无法选择对角线。它（具有残差网络的）应该是具有非常强的对角焦点，所发生的事情就是：位置信息最初添加在了模型的输入处，通过残差连接将位置信息传递到每一层，（而且后续层没有位置概念，这句话不是很明白），可以不需要再每一层都添加位置信息。再说一种情况。切断残差连接，但是每层注入位置信息，结果如上图右图，虽然出现了对角线，他们通过特征提取提取到了这个特点（就是注意力所实现的特征被提取到了）

训练细节

（没讲，大家自己看看吧）

• ADAM优化器具有学习速率预热（预热+指数衰减）
• 在每个层的训练过程中在添加剩余层范数之前退出
• 注意力层dropout（一些实验）（应该就是类似和神经网络dropout层差不多的意思吧？）
• 检查点平均标签平滑
• 波束搜索和长度偏置自回归译码

（很多概念不太懂，可能翻译的也不太准）

Self-Similarity, Image and Music Generation

 Self-similarity in images

图像中有许多相似的地方（不同的叶子，不同的纹理图案），可能他们位置、比例不同

 

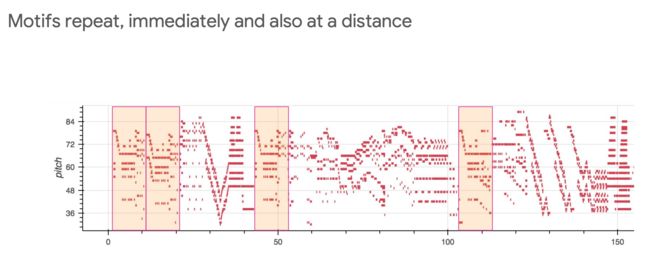
Self-similarity in music

音乐中也一样有许多重复或者相似的节拍

自我注意力可以帮助我们建立像图像、音乐这种其他对象吗？

我们采取的方法是标准自回归概率建模或概率图建模，而不是gan/对抗神经网络

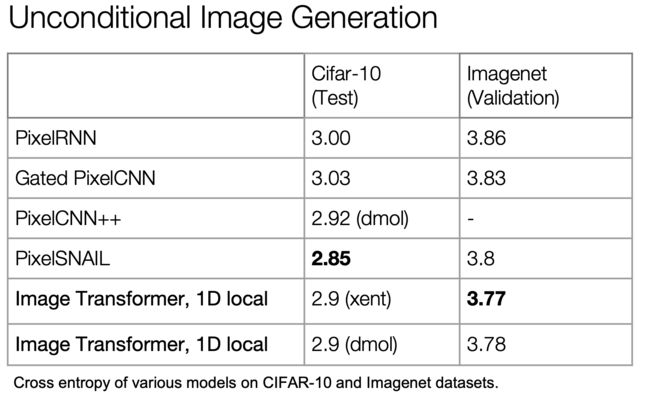
概率图像生成

模拟像素的联合分布，把它变成一个序列建模问题，分配概率允许度量泛化

RNN和CNN是最先进的（PixelRNN，PixelCNN），合并门控的CNNs现在在质量上与RNN相匹配，由于并行化，CNNs要快得多

图像的长期依赖关系很重要(例如对称性)，可能随着图像大小的增加而变得越来越重要，使用CNNs建模长期依赖关系需要考虑两个问题：多层可能使训练更加困难、大卷积核参数会使计算成本相应变大

Texture Synthesis with Self-Similarity/纹理合成

Non-local Means

（好像讲的去噪）两个例子主要说明了一下如何评价相似？（没太听懂emmmm）

以前的一些工作

Self-attention:

Parikh et al. (2016), Lin et al. (2016), Vaswani et al. (2017)

Autoregressive Image Generation:

A Oord et al. (2016), Salimans et al. (2017)

 

Self-attention

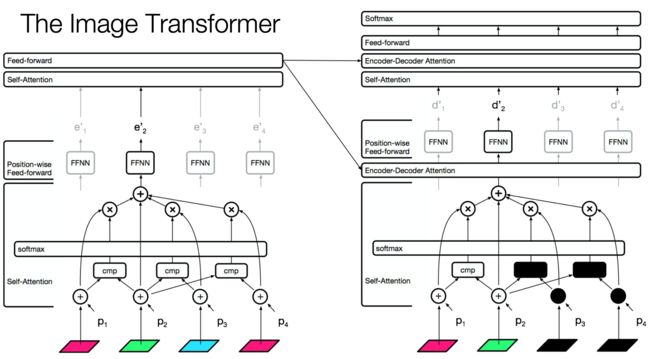
The Image Transformer

（与处理文本的类似，只是单词变成了像素值，还有一点机构需要调整，但是基本上大致相同）

Combining Locality with Self-Attention/组合局部性

有两种rasterization（光栅化？点阵化过程？我太会翻译。。。）

• 将注意力窗口限制为本地范围
• 由于空间局部性，这在图像中是很好的假设

光栅化貌似是一只局部捕捉的意思（不是很确定）

如下图

评价如下：

最右侧是原始图片，其他的是数据增强的结果（数据增强主要是旋转、倍缩、剪裁、改变色调、加噪声等），这样我们的数据集更大了，且更具有多样性了

Music generation using relative self-attention/利用相对自我注意的音乐生成

音乐和语言的原始表现

最初的表现就是音符吧

传统的 RNN 模型需要大量的压缩，将长序列嵌入到固定长度的向量中

RNN生成的音乐对于给的样本具有一定的重复性，难以处理长距离

而注意力机制一开始非常好，但是后面（超出训练长度后）也逐渐恶化（图中黑色聚集的部分就是开始恶化），但是整体与主题保持一致

音乐注意力机制（注意力机制针对音乐数据进行的微调的机制）则非常好了

灰色部分是主题发生的地方，彩色线则是注意力，可以发现对主题部分有许多注意力头在关注（上述图是正在预测～）

（这里的那个动画太np了，也非常适合我们理解注意力如何具体工作的）（后面没怎么听懂。。。）

• 移动的固定过滤器捕获相对距离
• Music Transformer使用平移不变性来携带超过其训练长度的关系信息，进行信息传递

• 位置之间的相关性
• 但是音乐中的序列长度通常很长（翻译可能几十个，但是音乐往往几千）

一些指标

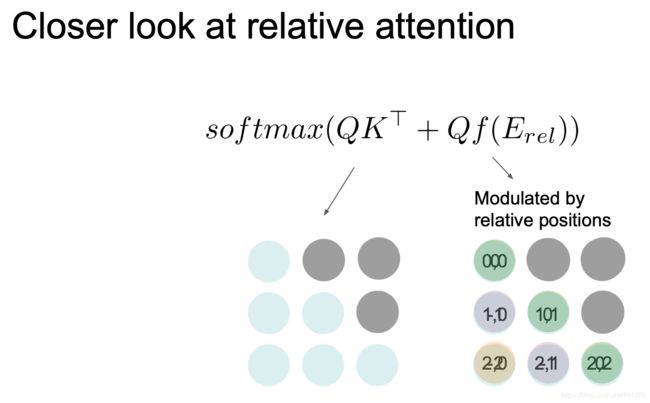
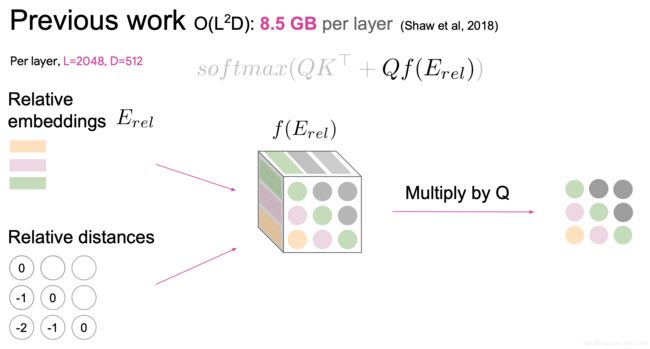
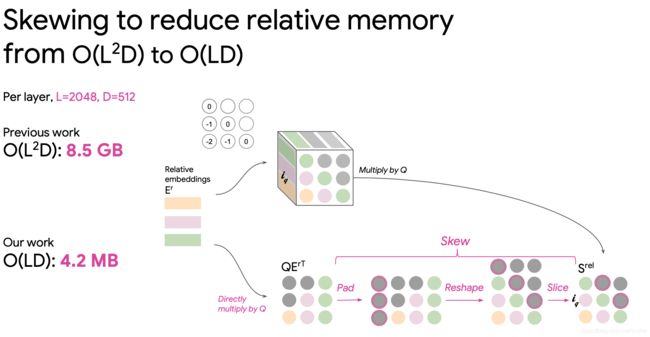
由于音乐非常大，上述是原来的方案，构建一个3D张量，记忆力非常大，因为对每一对都计算相对距离

实际上我们可以直接乘以查询和嵌入距离，我们有相对距离的排序查询，但是我们需要按键排序查询，这也就将相对距离转化为绝对距离，转换过程如下图：（明显小的太多了）

总结

所以相对注意力一直很强的机制，在音乐、机器翻译上表现非常好

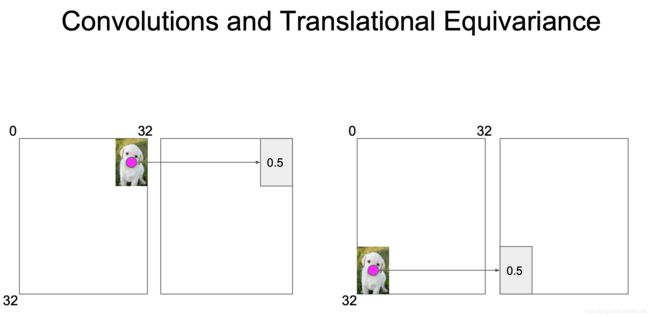
一个很有趣的现象，如下图：

卷积实现平移等价，在红点上计算特征，这个和位置无关，同样的卷积在翻译是也有这样的等价（貌似这个开发者想表达的意思是注意力也可以吗？）

还有个有趣的现象是，如下图

相对注意力机制可以发现一些关系（蓝色是水果关系，红色是公司关系）

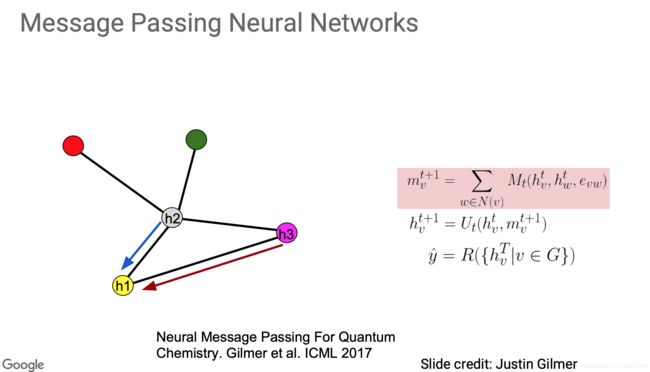
在消息传递神经网络中也表现很好，消息传递神经网络结构和其传递函数如下图

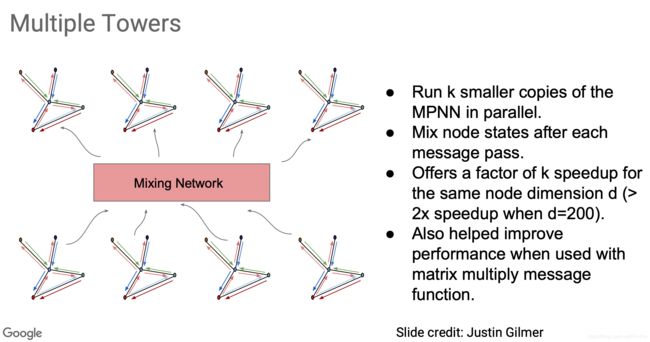
一个名为 Multiple Towers的有趣概念，类似于多头注意力机制，结构如下

最后总结

模型任意两个位置之间的路径长度都是恒定路径长度
没有边界的内存（在有限的数据集和空间中，模型记忆力随着序列增长而增长）
可以并行化
对自相似性进行建模（类似图像中重复的地方或者音乐中重复的节奏等）
相对注意力能够表达时间、音乐。平价转移可以自然延伸至图表

目前还有个自我注意力的研究领域：对于较少的自回归生成（应该没翻译错。。。）

还推荐了一些论文

转移学习

转移学习中自我注意力机制也是有益的在OpenAI和BERT中的GPT两个经典案例中

还用于演讲

在演讲中自我注意力机制也有很多成功的案例

自我监督也是非常有效的

不需要大型标签数据集，了解转移，转移正变得很成功（与BERT等模型在NLP中相比较）

未来展望