在数组中找出三个不重叠的固定长度的子数组，要求这三个子数组的和最大

题目

题目如题，举个例子：
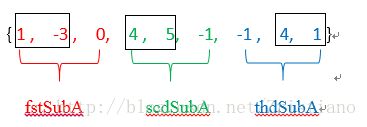
数组Array{ 1 , -3 , 0, 4 , 5, -1, -1 , 4, 1 }从中找出长度为2的三个子数组，和最大。
则能找出的结果就是{ 1 -3 ( 0 4) (5 -1) -1 (4 1) }

思路

这题比较麻烦，没什么好的办法，一种是穷举，时间复杂度O(n^3)，不太好。暂时想到的好点的是动态规划，但只有部分步骤用到了dp。

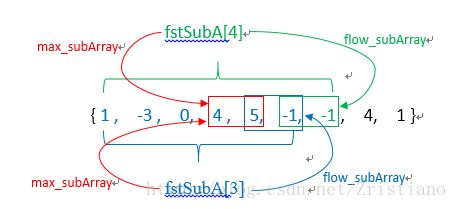
做这道题前先参考了一下这个问题：求一维数组中不重叠的两个子数组的最大和1。为了方便说明，假设子数组的固定长度为2。为了找出3个不重叠的子数组，可以将Array分成三部分: Array { fstSubA, scdSubA, thdSubA }，sum最大的三个长度为2的子数组分别来自fstSubA，scdSubA，thdSubA部分(每部分的范围至少大于题目中要求的子数组的长度，此处为大于2)。如下图，从fstSubA, scdSubA, thdSubA三部分各选出最大的子数组{0,4}、{5,-1}、{4,1}，sum为13 就是题目要求的子数组。

不同的划分有不同的结果，如下图，从各个划分部分选出的最大子数组{1,-3}、{4,5}、{4,1}的sum为12，小于上图的三个子数组的和。

要得到最优的子数组，则必须遍历所有不同的划分，找出最优解。不管怎么划分，fstSubA的左边界始终是Array的左边界，thdSubA的右边界始终是Array的右边界，scdSubA的边界则是fstSubA的右边界到thdSubA的左边界，因此可以通过fstSubA和thdSubA来确定scdSubA的范围。可以将算法过程分为以下几步：

• 通过dp方法算出所有fstSubA可能范围的最大子数组信息，保存下来
• 通过dp方法算出所有thdSubA可能范围的最大子数组信息，保存下来
• 遍历所有的fstSubA和thdSubA的组合
  
  • 通过确定的fstSubA和thdSubA算出对应的scdSubA的最大子数组信息
  • 对比保存sum最大的fstSubA、scdSubA、thdSubA的子数组信息

子数组信息定义结构体SingleSum来表示：

struct SingleSum{
    int maxSum = 0;  //（数组在）当前范围内的最大子数组的sum
    int flowSum = 0; //（数组在）当前范围内的离变动边界最近的子数组的sum
    int firstIdx;   //（数组在）当前范围内的最大子数组在整个Array的起始位置
};

步骤 1 - 算出所有fstSubA可能范围的最大子数组信息

Array{ 1 , -3 , 0, 4 , 5, -1, -1 , 4, 1 }的fstSubA的取值范围为：[{1 , -3 }, {1 , -3 , 0},…,{ 1 , -3 , 0, 4 , 5}]。因为scdSubA和thdSubA必须存在，所以fstSubA的取值范围不能包括Array里最右边四个元素。用SingleSum的结构体数组fstSubA[i]表示fstSubA第i个取值范围内的最大子数组信息，比如fstSubA[0]表示的是{1，-3}的最大子数组信息，fstSubA[1]表示的是{1 , -3 , 0}最大子数组信息 … fstSubA[3]表示的是{1 , -3 , 0, 4 , 5}最大子数组信息。具体信息如下：

fstSubA [ 0 ]

变量	值	意义
maxSum	-2	{1，-3}内的最大子数组是{1，-3}，maxSum = 1-3 = 2
flowSum	-2	fstSubA的变动边界为右边界(左边界固定为Array的左边界),离右边界最近的子数组是{1,-3},flowSum = 1-3 =2
firstIdx	0	最大子数组在Array中的起始位置，{1,3}在Array中的起始位置是0

---

fstSubA[ 1 ]

变量	值	意义
maxSum	-2	{1，-3 , 0}内的最大子数组是{1，-3}，maxSum = 1-3 = 2
flowSum	-3	离右边界最近的子数组是{-3,0}, flowSum = -3+0 = -3
firstIdx	0	最大子数组在Array中的起始位置，{1,3}在Array中的起始位置是0

---

保存flowSum是为了在循环过程中, 求出当前数组范围内可能的最大子数组的值。根据动态规划的思想，当前取值范围的fstSubA内的最大子数组的sum，要么等于上一个取值范围的fstSubA内的最大子数组sum，要么等于当前最右边的子数组的sum，因为fstSubA的取值范围每加1，影响的只有最右边的子数组的sum。比如：{1 , -3 , 0, 4 } –> {1 , -3 , 0, 4 ,5}， 右边数组的最大子数组要么是左边数组的最大子数组{0,4},要么是其最右边(离变动边界最近)的子数组{4,5}。
用a[i]表示数组Array的第i个元素，则可以得出dp的状态转移方程:

fstSubA[i].maxSum=max(fstSubA[i−1].maxSum,fstSubA[i].flowSum)

其中：

fstSubA[i].flowSum=fstSubA[i−1].flowSum−a[i−1]+a[i−1+2]

a[i-1+2]里的+2是因为上文假设了子数组的固定长度为2

---

步骤 2 - 算出所有thdSubA可能范围的最大子数组信息

thdSubA的算法和fstSubA类似，区别是遍历过程由右向左，变动边界在左边。{ 1 , -3 , 0, 4 , 5, -1, -1 , 4, 1 } 数组Array里的thdSubA的取值范围为：[{4, 1 }, {-1 , 4, 1},…,{ 5, -1, -1 , 4, 1 }]。比如 thdSubA[2]的取值范围为{ 5, -1, -1 , 4}

thdSubA[ 2 ]

变量	值	意义
maxSum	4	{5, -1, -1 , 4}内的最大子数组是{5，-1}，maxSum = 5-1 = 4
flowSum	4	thdSubA的变动边界为左边界(右边界固定为Array的右边界),离左边界最近的子数组是{5,-1},flowSum = 5-1 = 4
firstIdx	4	{5,-1}在Array中的起始位置是4

---

dp的状态转移方程和步骤一类似：

thdSubA[i].maxSum=max(thdSubA[i−1].maxSum,thdSubA[i].flowSum)

区别在flowSum的计算方向和 fstSubA是相反的：（count为Array的长度）

thdSubA[i].flowSum=thdSubA[i−1].flowSum−a[(count−i]+a[count−i−2]

---

步骤 3 - 算出scdSubA的最大子数组信息

通过步骤1、2已经得到了两个数组 fstSubA[i]、thdSubA[i]，根据指定i的fstSubA和thdSubA，可以得出scdSubA的取值范围，找出此scdSubA的最大子数组，这样对于每一个给定的i，都有fstSubA、scdSubA、thdSubA各自的最大子数组 max_fstSubA、max_scdSubA、max_thdSubA 组成一组解，遍历所有的i，就可以得到所有的解，从中找sum最大的解就不难了。

例如： 对于Array{1 , -3 , 0, 4 , 5, -1, -1 , 4, 1}， 当 i=1 时，fstSubA的取值范围为{ 1 , -3 , 0 }，thdSubA的取值范围为 { -1 , 4, 1 } ，则scdSubA的取值范围是{ 4 , 5, -1 }。此范围内的fstSubA的最大子数组信息在前面已经算出，为 fstSubA[1]，同理thdSubA的最大子数组信息为thdSubA[1]。scdSubA在给定的取值范围内找出最大子数组信息的算法可参照fstSubA的算法。

---

核心代码

#define INT_MIN 0x80000000;
typedef struct SingleSum {
    int maxSum = 0;  //（数组在）当前范围内的最大子数组的sum
    int flowSum = 0; //（数组在）当前范围内的离变动边界最近的子数组的sum
    int firstIdx;   //（数组在）当前范围内的最大子数组在整个Array的起始位置
}*SglSum;

/*找出数组array中,[start,end]区间内的长度为length的子数组，要求此子数组的sum最大*/
SglSum find_large_sum_sub(int *array, int start, int end, int length);

/*找出thdSubA所有的最大子数组信息*/
SglSum find_large_sum_sub_inverse(int *array, int count, int length);

/*
找出数组array中,三个不重叠的最大子数组，
@array
@count 数组array的长度
@length 子数组的长度
*/
void find_3_large_subArray(int* array, int count, int length)
{
    if (count < 3 * length)
    {
        cout << "数组长度不够" << endl;
        return;
    }
    SglSum fstSubArray = find_large_sum_sub(array, 0, count - 1, length); //fstSubA[i]
    SglSum thdSubArray = find_large_sum_sub_inverse(array, count, length); //thdSubA[i]

    //用户暂存每次遍历后得到的当前3个最大子数组
    SglSum fst_large_sub = NULL, scd_large_sub = NULL, thd_large_sub = NULL;
    SglSum scdSubArray;
    int sum = INT_MIN;

    for (int i = 0; i <= count - 3 * length; i++)
    {
        for (int j = 0; j <= count - 3 * length - i; j++)
        {
            scdSubArray = find_large_sum_sub(array, i + length, count - j - length - 1, length);
            // scdSubArray里存储array余下数列的最大子数组信息的元素的索引
            int scdMaxIdx = count - j - length - (i + length) - length;
            int tempSum = fstSubArray[i].maxSum + thdSubArray[j].maxSum
                          + scdSubArray[scdMaxIdx].maxSum;
            if (tempSum > sum)
            {
                fst_large_sub = fstSubArray + i;
                scd_large_sub = scdSubArray + scdMaxIdx;
                thd_large_sub = thdSubArray + j;
                sum = tempSum;
            }
        }
    }
    if (fst_large_sub == NULL || scd_large_sub == NULL || thd_large_sub == NULL)
    {
        return;
    }
    cout << "最大子数组集是： ";
    for (int i = 0; i < length; i++)
    {
        cout << array[fst_large_sub->firstIdx + i] << " ";
    }
    cout << "   ";
    for (int i = 0; i < length; i++)
    {
        cout << array[scd_large_sub->firstIdx + i] << " ";
    }
    cout << "   ";
    for (int i = 0; i < length; i++)
    {
        cout << array[thd_large_sub->firstIdx + i] << " ";
    }

    cout << endl << "sum is " << sum;
}

SglSum find_large_sum_sub(int *array, int start, int end, int length)
{
    int count = end - start + 1;
    SglSum subArray = new SingleSum[count - length + 1];
    for (int i = 0; i < length; i++)   //算出第一个subArray
    {
        subArray[0].flowSum += array[start + i];
    }
    subArray[0].maxSum = subArray[0].flowSum;
    subArray[0].firstIdx = start;
    for (int i = 1; i <= count - length; i++)
    {
        subArray[i] = subArray[i - 1];
        //浮动sum = 上个浮动sum - 剔除的边界元素 + 新增的边界元素
        subArray[i].flowSum = subArray[i].flowSum - array[start + i - 1] 
                              + array[start + i - 1 + length];  
        if (subArray[i].flowSum>subArray[i].maxSum)
        {
            subArray[i].maxSum = subArray[i].flowSum;
            subArray[i].firstIdx = start + i;
        }
    }
    return subArray;
}

SglSum find_large_sum_sub_inverse(int *array, int count, int length)
{
    SglSum subArray = new SingleSum[count - 3 * length + 1];
    for (int i = count - length; i < count; i++)   //算出第一个subArray,从后算起
    {
        subArray[0].flowSum += array[i];
    }
    subArray[0].maxSum = subArray[0].flowSum;
    subArray[0].firstIdx = count - length;
    for (int i = 1; i <= count - 3 * length; i++)
    {
        subArray[i] = subArray[i - 1];
        subArray[i].flowSum = subArray[i].flowSum - array[count - i] + array[count - i - length];
        if (subArray[i].flowSum > subArray[i].maxSum)
        {
            subArray[i].maxSum = subArray[i].flowSum;
            subArray[i].firstIdx = count - length - i;
        }
    }
    return subArray;
}

测试用例

find_3_large_subArray(array, sizeof(array)/sizeof(array[0]), length)  //length为子数组长度

1. array = { 1, -3, 0, 4, 5, -1, -1, 4, 1 } ， length=2：
   

2. array = {5,5,2,-8,-10,2,5,-12,10,3,-8,0,-2,-4,-5,15,5,-2,4,2,-3,4,8,-1,5,-9} ，length=2：
   

3. array = {5,5,2,-8,-10,2,5,-12,10,3,-8,0,-2,-4,-5,15,5,-2,4,2,-3,4,8,-1,5,-9} ，length=3：
   

4. array = {5,5,2,-8,-10,2,5,-12,10,3,-8,0,-2,-4,-5,15,5,-2,4,2,-3,4,8,-1,5,-9} ，length=4：
   

---

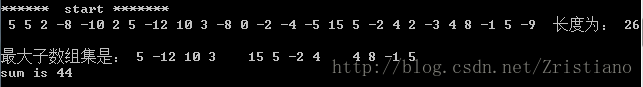
时间复杂度分析

步骤1、2、3顺序执行，步骤1、2中计算fstSubA、thdSubA的最大子数组的时间复杂度为O(n)，计算scdSubA最大子数组的操作在遍历所有fstSubA、thdSubA划分的循环中，因此步骤三的时间复杂度为O(n²/2-n/2)，整个算法的时间复杂度为O(n²)。

---

1. http://www.cnblogs.com/litao-tech/p/4163576.html. ↩