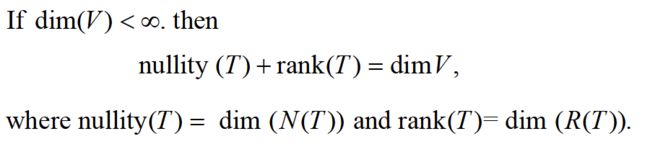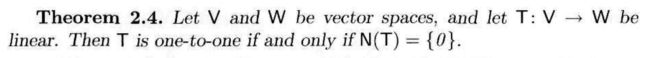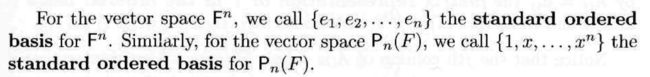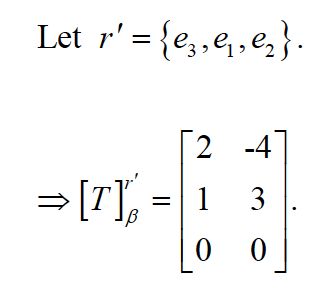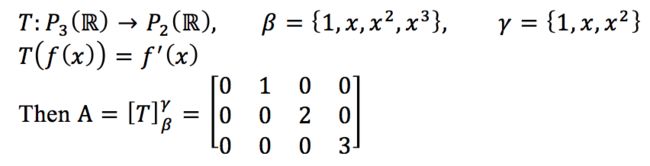线性代数笔记（2）：线性变换及其矩阵表示

一、线性变换的定义

Definition: Let V and W be vector spaces. We call a function T : V →W a linear transformation (or linear) from V to W if for all x, y ∈ V and c ∈ F , we have (a) T(x+y) = T(x) + T(y) and (b) T(cx) ∈ cT(x).

在实际中，我们常常利用下面这个等价关系啦证明变换满足线性：

二、像与核

（也可以参考http://blog.csdn.net/baimafujinji/article/details/6474272）

Definitions： T : V →W is linear.

1. N(T) the null space (or kernel) of T，N(T)={x ∈ V: T(x) = 0} .
2. R(T) the range (or image) of T,  R(T)={T(x): x ∈ V} = {y ∈ W:  ∃ x ∈ V with T(x)=y}
   

Thm2.1： T : V →W, where V, W are vector spaces and T is linear，那么可以推出：R(T) and N(T) are subspaces of W and V, respectively.

Thm2.2：T : V →W, T is 线性变换，V和W是向量空间，如果 β={v₁,v₂, ..., v_n} 是V的一个基底，那么则有

R(T) = Span(T(β)) = Span({T(v₁),T(v₂), ..., T(v_n)})。

定理2.2 告诉我们，如果把定义域的基底 β 用T转换后再张开，将得到值域。

三、维度理论（Dimension Theory）

Thm 2.3：T : V →W, T is 线性变换，

注意：如果有限维的条件被去掉，则结论不一定成立！

四、矩阵表示法

E.g.，

E.g.，假设在3维空间里有一个元素x=(2,3,5)，然后我们还有一组基底β={u₁,u₂, u₃}，其中u₁=(1,0,0), u₂=(0,1,0),  u₃=(0,0,1)，显然此时我们的系数a₁=2, a₂=3, a₃=5，那么x关于β的坐标向量就是(2,3,5)。而且当基底改变时，这个坐标向量显然也会随之改变。

既然我们可以用坐标向量来表示一个向量空间中的元素，那么一个线性变换是否也可以有类似的表达呢，下面的方法告诉我们可以用矩阵来表示一个线性变换。

e.g., T: R²→R³. T(a₁,a₂)=(a₁+3a₂, 0, 2a₁ - 4a₂). β and r are standard ordered bases for R² and R³.

于是则有

如果我们改变基底的顺序，则有

五、线性变换组成的集合仍然是向量空间

上述定义的意思等同于 L(V, W) = {T: T: V→W}，也即是L(V, W) 是一个集合，集合中收集的元素是各种各样的T，每一个T都是一个从V到W的线性变换。更进一步地，我们还能证明 L(V, W)是一个向量空间。既然L(V, W) 是一个向量空间，那么我们就要定义加法和乘法。具体的定义方法如下：

如果我们采用上述方法来定义加法和乘法，那么下面的定理其实就表明L(V, W) 是一个向量空间。

最后我们还有如下结论：

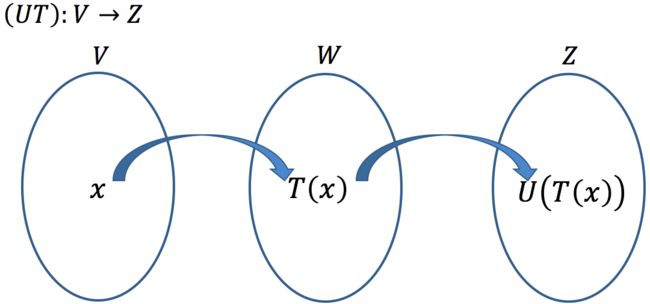
六、线性变换的合成

通常我们很难定义函数的乘法，但是却可以定义函数的合成（也就是复合函数），如下图示所

Thm 2.9: The composite of linear transformations is linear. （也就是说线性函数的合成仍然是线性的）

更进一步还有如下结论：

七：线性变换的合成等价于代表矩阵之相乘

下面这个定理也非常有用，它的意思是说——T为一个从V到W的线性变换，u是V中的一个元素，那么T(u)显然就是W中的一个元素。

r是W的ordered basis，所以[T(u)]_r就是T(u)这个元素相对于r的向量表示，而且它就等于T的矩阵表示（采用β和r作为基底）乘以u对于β的向量表示。

我们来看一个例子：

八、可逆

从矩阵的角度来说，对于一个矩阵A，如果存在一个逆矩阵A^-1，使得AA^-1=A^-1A=I，那么我们就说矩阵A是可逆的。更泛化的情况下，我们希望来讨论一个算子可逆的概念（联系一下函数可逆的概念）。

Thm 2.17：T是线性的，那么它的逆T^-1也是线性的。

下面这个定理告诉我们：如果一个算子是可逆的，那么它的矩阵表示也是可逆的。

Thm 2.18：T : V → W，T线性变换，β 和 γ 分别是V和W的ordered bases。Then

九、同构

注意：V is isomorphic to W 等价于 W is isomorphic to V. So we need only say that V and W are isomorphic or, symbolically, V ~ W.

由Thm 2.20很容易可以得到如下推论：

给定一个向量空集V，其维度dim(V)=n，β is an ordered basis for V. 我知道V和Fⁿ是彼此isomorphic的。这也就是说我们可以定义一个 isomorphism（注意isomorphism也是一个线性变换）from V to Fⁿ。下面这个定义和定理就给我们了一种最为简单的给出一个 isomorphism 的方法。

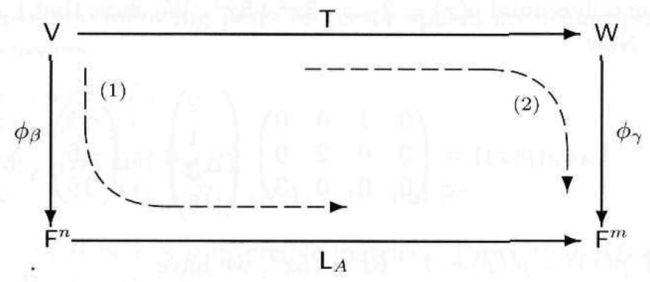
下图总结了我们前面已经学过的几个同构关系和彼此的转换，其中L_A是一个算子，它作用在x上，即L_A(x)，就等同于Ax，即L_A=Ax。

更准确地说，L_A中的A就是。而且，。

（本文完）

本文主要根据台湾交通大学开放课程线性代数（莊重 特聘教授主讲）之授课内容整理，并参考以下书籍：

【1】S.H. Friedberg, A.J. Insel, L.E Spence, 4th edition, Linear Algebra, Prentice-Hall, 2003

【2】David C. Lay. 刘深泉，等译. 线性代数及其应用（原书第3版），机械工业出版社，2005