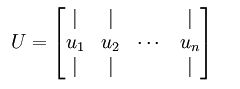Principal components analysis(PCA) 主成分分析

本文主要参考资料：

CS229 lecture notes by Andrew Ng
UFLDL主成分分析 by Andrew Ng
《机器学习实战》第13章“使用PCA来简化数据”

1. 运用背景

在机器学习中，PCA是一种常用的方法。其目的是将 n 维的原始数据近似的用 k 维来表示，而且近似表示后对数据的损失尽可能的小。我们可以假设原始的 n 维数据 x(i) 是由 k 维数据添加一些噪声后形成的，而PCA要做的就是找到这个 k 维表示。

举例来说，如果一份数据集代表车辆的特征，包括最大速度、扭矩等。其中有两个特征 xi 和 xj 均代表车辆的最大数据，但其中一个的单位是 km/h， 另外一个是 m/s。那么这两个特征就是强相关的，在将这份数据用于监督学习算法时，仅保留其中一个特征即可。PCA要做的就是自动的发现并去除这种冗余。

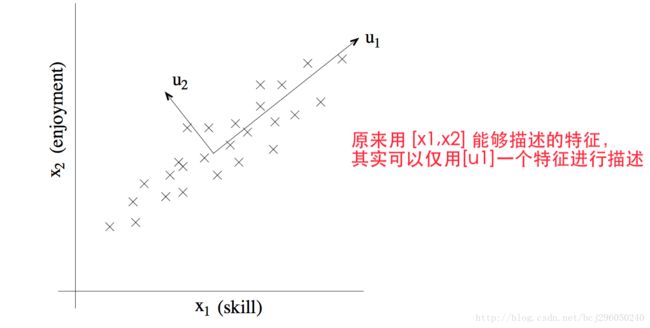
另外一份真实数据是有关飞行员的，描述飞行员有两个特征，第一个特征 xi 表示这个飞行员的技能，另外一个特征 xj 代表飞行员对飞行的热爱程度。调查发现，由于该种机型非常难以操控，因此只有对飞行非常热爱的飞行员才拥有高超的驾驶技术。因此特征 xi 和特征 xj 是强相关的。而相比于上一个例子来说，这种强相关是人难以发现的，需要PCA算法来自动发现这种冗余的特征。如下图所示，我们需要算法来自动的计算出 u1 方向，该方向是拥有最大方差的投影方向，与其正交的 u2 方向则拥有很小的数据方差，可以被当做噪声。

2. 数据预处理

1. 计算均值，使用下列公式，计算的结果是一个n维向量，向量中的每个元素是所有样本的相应特征的均值。
   
   μ=1m∑i=1mx(i)
2. 对每一个样本 x(i) ，计算其特征中心化后的结果，即
   x(i)=x(i)−μ
3. 计算第 j 维特征的方差（ jϵ[1,n] ）
   
   σ2j=1m∑i=1m(x(i)j)2
4. 对于每一个样本 x(i) ，另其每一维特征除以相应特征的标准差，使得每种特征的范围相同。即
   x(i)j=x(i)jσj

步骤1-2是零均值化数据，如果原始数据的均值为0，则可以省略该步骤，如时间序列数据、音频数据。步骤3-4对每一维特征的方差归一化，确保不同尺度的特征可以在分类中有相同的作用。如果数据为图像数据，每一个像素点是一个特征，特征的尺度都在0-255之内，则不需要做3-4步。

3.算法步骤

解决方法是寻找单位向量 u 使得数据在该方向上的投影的方差能够最大化。形象的说，原始数据的每一维特征有一定的方差，我们想要选择一个方向 u 使得数据大致分布在该方向上，在该方向的投影数据能够保留尽可能多的方差。

假设原始数据的特征是二维的，并且已经经过均值归零化处理和方差归一化处理，如下图所示。

当选择一个新的投影反向 u 后，我们将原始数据点向方向 u 进行投影操作。

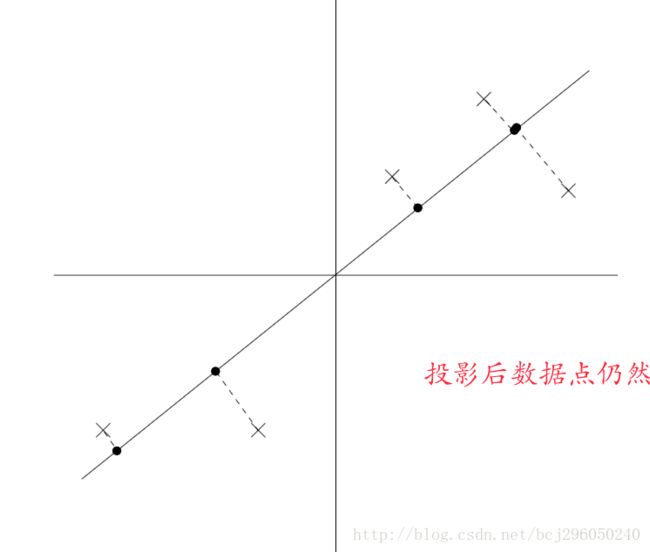
我们可以看到投影后的数据仍然保持着较大的方差，数据点距离原点较远。相反，如果按照下面的方式选择投影方向，则投影后数据点之间的不同很少被保留下来，数据点普遍向原点靠近。

假设基向量 u 为单位向量，则向量 x 投影到 u 后的长度为 xTu 。假设 x(i) 是一个数据点，则向方向 u 上的投影点相对于原点的距离为 xTu 。PCA的目的是最大化这一投影距离：

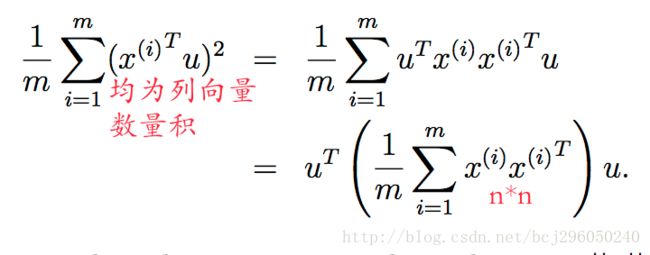
根据线性代数的知识，在 ||u||2=1 的条件下求该式最大化情况下的 u ，则 u 为 Σ=1m∑mi=1x(i)x(i)T 的特征向量，而 Σ 正好是数据的协方差矩阵（在均值为0的条件下）。

有关于协方差矩阵的相关知识可以参考这两篇文章：
1. http://www.cnblogs.com/chaosimple/p/3182157.html
2. http://www.cnblogs.com/cezorzhao/archive/2013/01/11/xiefangcha.html

Σ 协方差矩阵的特征向量按列排放构成矩阵 U 如下：

其中， u1 是主特征向量（对应最大的特征值）， u2 是次特征向量，以此类推。另计 λ1,λ2,λ3...λn 为相应的特征值。

旋转数据

可以将 x 用 (u1,u2) 基表示为:

xrot=UTx=[uT1xuT2x]

一般而言，运算 UTx 表示旋转到基 u1,u2...un 之上的训练数据。矩阵 U 有正交性，即满足 UTU=UUT=I ，所以如果想将旋转后的向量 xrot 还原为原始数据 x ，将其左乘矩阵 U 即可。

Uxrot=UUTx=x

数据降维

还原近似数据

选择主成分个数

对图像数据应用PCA算法

为使PCA算法能够有效工作，通常我们希望所有的特征 x1,x2,x3,...,xn 都有相似的取值范围（并且均值接近于0）。如果你曾在其他应用中使用过PCA算法，你可能也知道有必要单独对每个特征进行预处理，即通过估算每个特征 xj 的均值和方差，而后将其取值范围规整为零均值和单位方差。但是对于大部分图像而言，却不需要进行这样的预处理。假设在自然图像上训练算法，此时特征 xj 代表的是相似 j 的值。所谓“自然图像”，不严格的说，是指人或动物在他们一生中所见的那种图像。

在自然图像上进行训练时，对每一个像素单独估计均值和方差的意义不大，因为理论上图像上任一部分的统计特性都应该和其他部分相同，图像的这种特性称为平稳性。

具体而言，为使PCA算法正常工作，我们通常要满足以下要求：
（1）特征的均值大致为0
（2）不同特征的方差彼此相似。

对于自然图片，即使不进行方差归一化操作，条件（2）也满足，故而我们不再进行任何方差归一化操作（对于音频数据，如声谱、文本数据、词袋向量等，我们通常也不进行方差归一化）。实际上，PCA算法对输入数据具有缩放不变性，无论输入数据被如何放大（或缩小），返回的特征向量都不改变。更正式的说：如果将每个特征x都乘以某个正数（即所有特征量被放大或缩小相同的倍数），PCA的输出特征向量都将不会发生改变。

既然我们不做方差归一化，那么唯一还需要进行的规整化操作就是均值规整化，其目的是保证所有特征的均值都在0附近。根据应用，在大多数条件下，我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中，图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式的说，我们队图像块的平均亮度值不感兴趣，所以可以减去这个值来进行均值规整话。

具体的步骤是，如果 x(i)ϵRn 代表16*16的图像块的亮度（灰度）值（n=256），可用如下算法来对每幅图像进行零均值化操作：

μ(i):=1n∑j=1nxij

x(i)j:=x(i)j−μ(i),(for−all−j)

即对某幅图像求其所有像素的均值，再令该图像的所有像素减去这个均值。

注意：1）对每个输入图像块 x^{(i)} 都要单独直行上面两个步骤，2）这里的 μ(i) 指的是图像块 x(i) 的平均亮度值。尤其需要注意的是，这和为每个像素 xj 单独估算均值是两个完全不同的概念。

如果你处理的图像是非自然图像（比如，手写文字，或者白背景正中摆放单独物体），其他规整化操作就值得考虑了，而那种做法最合适也取决于具体应用场合。但对自然图像而言，对每幅图像进行上述的零均值规整化，是默认而合理的处理。