二叉搜索树 (binary search tree)
二叉搜索树 (binary search tree)
二叉排序树 (Binary Sort Tree),又称二叉查找树 (Binary Search Tree),亦称二叉搜索树。
symmetric [sɪ'metrɪk]:adj. 对称的,匀称的
0. 树
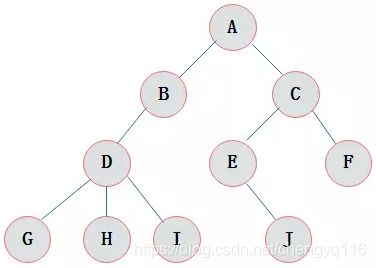
结点是构成复杂数据结构的基本组成单位。
树 (tree) 是 n (n >= 0) 个结点的有限集。n = 0 时称为空树。在任意一颗非空树中,有且仅有一个特定的称为根 (root) 的结点。n > 0 时,根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
树的定义使用了递归的方式。
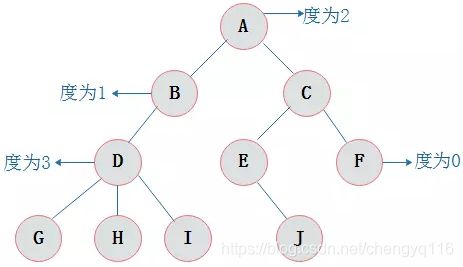
0.1 结点的度、关系、层次和深度
结点拥有的子树数目称为结点的度。
A 为 B 的双亲结点,B 为 A 的孩子结点。同一个双亲结点的孩子结点之间互称兄弟结点。结点 B 与结点 C 互为兄弟结点。
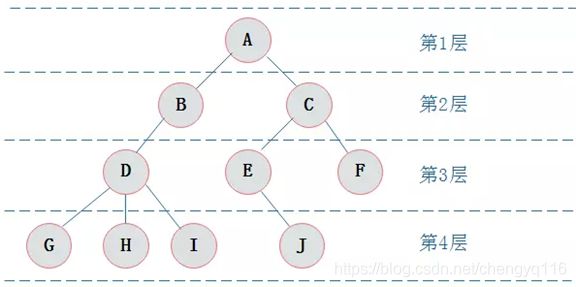
从根节点开始定义起,根为第一层。树中结点的最大层次数称为树的深度或高度。图示树的深度为 4。
1. 二叉搜索树 (binary search tree)
树是一种数据结构,它要么为空,要么具有一个值并具有零个或多个孩子 (child),每个孩子本身也是树。这个递归的定义正确地提示了一棵树的高度并没有内在的限制。二叉树 (binary tree) 是树的一种特殊形式,它的每个节点至多具有两个孩子,分别称为左孩子 (left) 和右孩子 (right)。
二叉搜索树具有一个额外的属性:每个节点的值比它的左子树的所有节点的值都要大,但比它的右子树的所有节点的值都要小。注意这个定义排除了树中存在值相同的节点的可能性。这些属性使二叉搜索树成为一种用关键值快速查找数据的优秀工具。
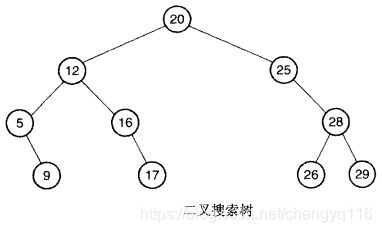
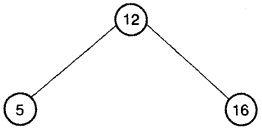
1.1 二叉搜索树 (binary search tree) 示例
这棵树的每个节点都正好具有一个双亲节点 (它的上层节点),零个、一个或两个孩子 (直接在它下面的节点)。唯一的例外是最上面的那个节点,称为树根,它没有双亲节点。没有孩子的节点被称为叶节点 (leafnode) 或叶子 (leaf)。在绘制树时,根位于顶端,叶子位于底部。注意这和自然世界中根在底叶在上的树实际上是颠倒的。
1.2 在二叉搜索树中插入
当一个新值添加到一棵二叉搜索树时,它必须被放在合适的位置,继续保持二叉搜索树的属性。幸运的是,这个任务是很简单的。其基本算法如下所示:
如果树为空:
把新值作为根节点插入
否则:
如果新值小于当前节点的值:
把新值插入到当前节点的左子树
否则:
把新值插入到当前节点的右子树
这个算法的递归表达正是树的递归定义的直接结果。
为了把 15 插入到上图的树,把 15 和 20 比较。15 更小,所以它被插入到左子树。左子树的根为 12,因此重复上述过程:把 15 和 12 比较。这次 15 更大,所以它被插入到 12 的右子树。现在我们把 15 和 16 比较。15 更小,所以插入到节点 16 的左子树。但这个子树是空的,所以包含 15 的节点便成为节点 16 的新左子树的根节点。
由于递归在算法的尾部出现 (尾部递归),所以我们可以使用迭代更有效地实现这个算法。
1.3 从二叉搜索树删除节点
从树中删除一个值比从堆栈或队列删除一个值更为困难。从一棵树的中部删除一个节点将导致它的子树和树的其余部分断开 - 我们必须重新连接它们,否则它们将会丢失。
我们必须处理三种情况:删除没有孩子的节点;删除只有一个孩子的节点;删除有两个孩子的节点。第 1 个情况很简单,删除一个叶节点不会导致任何子树断开,所以不存在重新连接的问题。删除只有一个孩子的节点几乎同样容易:把这个节点的双亲节点和它的孩子连接起来就可以了。这个解决方法防止了子树的断开,而且仍能维持二叉搜索树的次序。
最后一种情况要困难得多。如果一个节点有两个孩子,它的双亲不能连接到它的两个孩子。解决这个问题的一种策略是不删除这个节点,而是删除它的左子树中值最大的那个节点,并用这个值代替原先应被删除的那个节点的值。
1.4 在二叉搜索树中查找
由于二叉搜索树的有序性,所以在树中查找一个特定的值是非常容易的。下面是它的算法:
如果树为空:
这个值不存在于树中
否则:
如果这个值和根节点的值相等:
成功找到这个值
否则:
如果这个值小于根节点的值:
查找左子树
否则:
查找右子树
这个递归算法也属于尾部递归,所以采用迭代方案来实现效率更高。
当值被找到时你该做些什么呢?这取决于用户的需要。有时,用户只需要确定这个值是否存在于树中。这时,返回一个真/假值就足够了。如果数据是一个由一个关键值字段标识的结构,用户需要访问这个查找到的结构的非关键值成员,这就要求函数返回一个指向该结构的指针。
1.5 树的遍历
同堆栈和队列不同,树并未限制你只能访问一个值。因此树具有另一个基本操作 - 遍历 (traversal)。当你检查一棵树的所有节点时,你就在遍历这棵树。遍历树的节点最常用的是前序 (pre-order)、中序 (in-order)、后序 (post-order) 和层次遍历 (breadth-first)。
前序 (pre-order) 遍历检查节点的值,然后递归地遍历左子树和右子树。例如,上面这棵树的前序遍历将从处理 20 这个值开始。然后我们再遍历它的左子树:
在处理完 12 这个值之后,我们继续遍历它的左子树
并处理 5 这个值,节点 5 的左右子树皆为空,我们就完成了这棵子树的遍历。
在完成节点 12 的左子树遍历之后,我们继续遍历它的右子树:
并处理 16 这个值,节点 16 的左右子树皆为空,这意味着我们已经完成了根为 16 的子树和根为 12 的子树的遍历。
在完成了节点 20 的左子树遍历之后,下一个步骤就是处理它的右子树:
处理完 25 这个值以后便完成了整棵树的遍历。
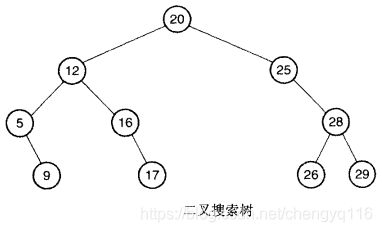
上图的二叉搜索树。当检查每个节点时打印出它的值,那么它的前序遍历的输出结果将是:20, 12, 5, 9, 16, 17, 25, 28, 26, 29。
中序遍历首先遍历左子树,然后检查当前节点的值,最后遍历右子树。上图的树的中序遍历结果将是:5, 9, 12, 16, 17, 20 , 25, 26, 28, 29。
后序遍历首先遍历左右子树,然后检查当前节点的值。上图的树的后序遍历结果将是:9, 5, 17, 16, 12, 26, 29, 28, 2 , 20。
最后,层次遍历逐层检查树的节点。首先处理根节点,接着是它的孩子,再接着是它的孙子,依次类推。用这种方法上图的树的次序是:20, 12, 25, 5, 16, 28, 9, 17, 26, 29。虽然前三种遍历方法可以很容易地使用递归来实现,但最后这种层次遍历要采用一种使用队列的迭代算法。
1.6 二叉搜索树模块的接口
下面程序的接口提供了用于把值插入到一棵二叉搜索树的函数的原型。它同时包含了一个 find 函数用于查找树中某个特定的值,它的返回值是一个指向找到的值的指针。它只定义了一个遍历函数,因为其余遍历函数的接口只是名字不同而己。
tree.h
/*
** Interface for a binary search tree module - 二叉搜索树模块的接口
*/
#define TREE_TYPE int /* Type of value in the tree - 树的值类型 */
/*
** insert
** Add a new value to the tree. The argument is the value to be added and must not already exist in the tree.
** 向树添加一个新值。参数是需要被添加的值,它必须原先并不存在于树中。
*/
void insert( TREE_TYPE value);
/*
** find
** Searches for a specific value, which is passed as the first argument.
** 查找一个特定的值,这个值作为第 1 个参数传递给函数。
*/
TREE_TYPE *find( TREE_TYPE value);
/*
** pre_order_traverse
** Does a pre-order traversal of the tree. The argument is a
** pointer to a callback function that will be called for each node in the tree, with the value passed as an argument.
** 执行树的前序遍历。它的参数是一个回调函数指针,它所指向的函数将在树中处理每个节点被调用,节点的值作为参数传递给这个函数。
*/
void pre_order_traverse(void (*callback)( TREE_TYPE value));
3. 编程总结
二叉搜索树 (BST) 是一种数据结构,它或者为空,或者具有一个值并拥有零个、一个或两个孩子 (分别称为左孩子和右孩子),它的孩子本身也是一棵 BST。BST 树节点的值大于它的左孩子所有节点的值,但小于它的右孩子所有节点的值。由于这种次序关系的存在,在 BST 中查找一个值是非常高效的。如果节点并未包含需要查找的值,你总是可以知道接下来应该查找它的哪棵子树。为了向 BST 插入一个值,你首先进行查找。如果值未找到,就把它插入到查找失败的位置。当你从 BST 删除一个节点时,必须小心防止把它的子树同树的其他部分断开。
树的遍历就是以某种次序处理它的所有节点。有 4 种常见的遍历次序。前序遍历先处理节点,然后遍历它的左子树和右子树。中序遍历先遍历节点的左子树,然后处理该节点,最后遍历节点的右子树。后序遍历先遍历节点的左子树和右子树,最后处理该节点。层次遍历从根到叶逐层从左向右处理每个节点。数组可以用于实现 BST,但如果树不平衡,这种方法会浪费很多内存空间。链式 BST 可以避免这种浪费。
- 使用断言检查内存是否分配成功是危险的。
- 数组形式的二叉树节点位置计算公式假定数组的下标从 1 开始。
- 把数据封装于对它进行操纵的模块可以防止用户不正确地访问数据。
- 与类型无关的函数没有类型检查,所以应该小心,确保传递正确类型的数据。
- 避免使用具有副作用的函数可以使程序更容易理解。
- 一个模块的接口应该避免暴露它的实现细节。
- 将数据类型参数化,使它更容易修改。
- 只有模块对外公布的接口才应该是公用的。
- 使用断言来防止非法操作。
- 几个不同的实现使用同一个通用接口使模块具有更强的可互换性。
- 复用现存的代码而不是对它进行改写。
- 迭代比尾部递归效率更高。
References
https://www.cs.rit.edu/~kar/pointers.on.c/